数学文卷·2017届山东省武城县第二中学高三下学期第一次月考（2017

数学文卷·2017届山东省武城县第二中学高三下学期第一次月考（2017

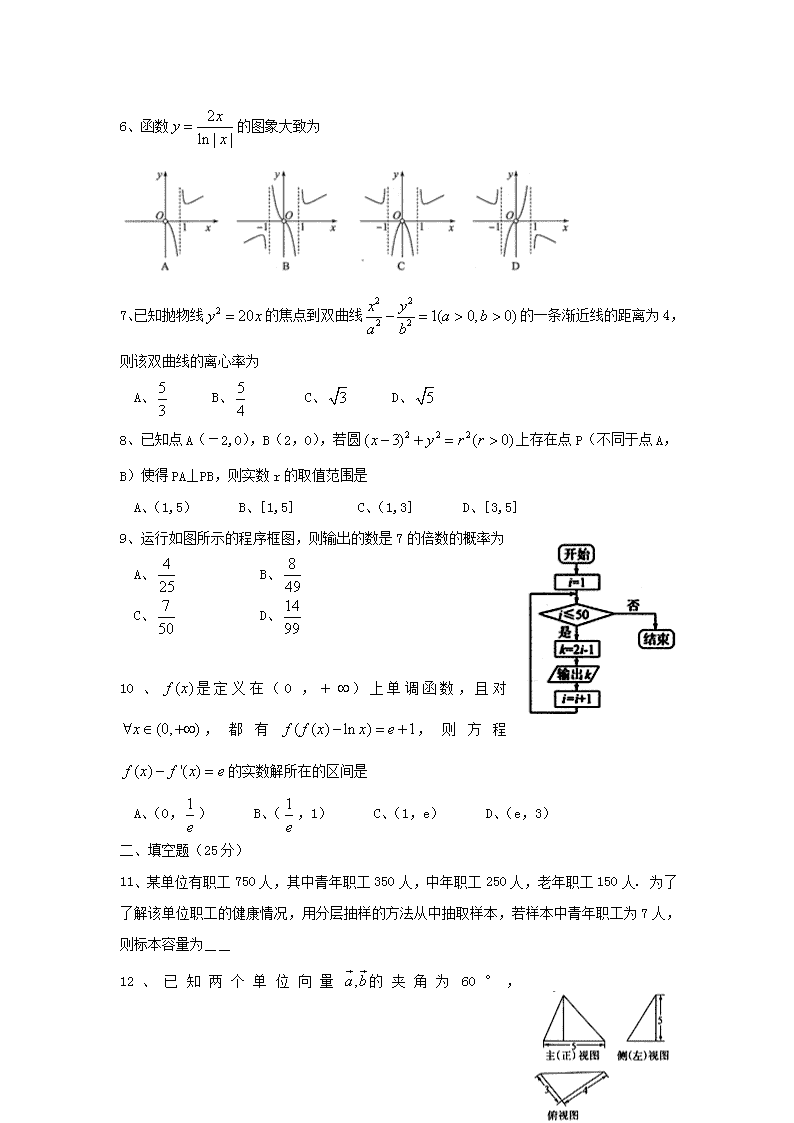
高三年级下学期第一次月考 数学（文）试题 一、选择题（50分）‎ ‎1、复数是虚数单位）的共轭复数为 ‎ A、　　　 B、　　　 C、　　　 D、‎ ‎2、若全集U＝R，集合A＝，B＝，则＝‎ A、　　　 B、‎ C、　　 D、‎ ‎3、已知p：“直线l的倾斜角”；q：“直线l的斜率k＞1”，则p是q的 A、充分不必要条件　　 B、必要不充分条件 C、充要条件　　　　　 D、既不充分也不必要条件 ‎4、为了增强环保意识，某校从男生中随机抽取了60人，从女生中随机抽取了50人参加环保知识测试，统计数据如下表所示，经计算＝7.822，则环保知识是否优秀与性别有关的把握为 优秀 非优秀 总计 男生 ‎40‎ ‎20‎ ‎60‎ 女生 ‎20‎ ‎30‎ ‎50‎ 总计 ‎60‎ ‎50‎ ‎110‎ 附：,‎ ‎0.500‎ ‎0.100‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ ‎0.455‎ ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ A、90%　　　B、95%　　　C、99%　　　B、99.9%‎ ‎5、已知，则 ‎　A、a＜b＜c　　B、c＜b＜a　　C、c＜a＜b　　　D、b＜c＜a ‎6、函数的图象大致为 ‎7、已知抛物线的焦点到双曲线的一条渐近线的距离为4，则该双曲线的离心率为 A、　　　B、　　　　C、　　　D、‎ ‎8、已知点A（－2,0），B（2，0），若圆上存在点P（不同于点A，B）使得PA⊥PB，则实数r的取值范围是 ‎　A、（1,5）　　　B、［1,5］　　　　C、（1,3］　　　D、［3,5］‎ ‎9、运行如图所示的程序框图，则输出的数是7的倍数的概率为 ‎　A、 B、‎ C、 D、‎ ‎10、是定义在（0，＋）上单调函数，且对，都有，则方程的实数解所在的区间是 ‎　A、（0，）　　　B、（，1）　　　C、（1，e）　　　D、（e，3）‎ 二、填空题（25分）‎ ‎11、某单位有职工750人，其中青年职工350人，中年职工250人，老年职工150人. 为了了解该单位职工的健康情况，用分层抽样的方法从中抽取样本，若样本中青年职工为7人，则标本容量为＿＿‎ ‎12、已知两个单位向量的夹角为60°，‎ 若，则正实数t＝　　‎ ‎13、某三棱锥的三视图如图所示，其侧（左）视图为直角三角形，则该三棱锥外接球的表面积为　　　　　　　‎ ‎14、已知满足，且的最大值是最小值的－2倍，则的值是　　　‎ ‎15、若直角坐标平面内两点P，Q满足条件①P、Q都在函数y＝f（x）的图象上；②P、Q关于原点对称，则对称点（P，Q）是函数y＝f（x）的一个“伙伴点组”（点对（P，Q）与（Q，P）看作同一个“伙伴点组”）．则下列函数中，恰有两个“伙伴点组”的函数是＿＿＿（填空写所有正确选项的序号）‎ 三、解答题 ‎16、（本小题满分12分）‎ ‎　某中学为了解某次竞赛成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本进行统计，请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题：‎ ‎（I）写出的值；‎ ‎（II）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学参加座谈，求所抽取的2名同学来自同一组的概率。‎ ‎17、（本小题满分12分）‎ 已知函数的最小正周期为3。‎ ‎（I）求函数的单调递增区间；‎ ‎（II）在ΔABC中，分别为角A，B，C所对的边，，，并且，求cosB的值。‎ ‎18、（本小题满分12分）‎ 在四棱锥P-ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC中点，又PA＝4，AB＝4，∠CDA＝120°，点N在线段PB上，且PN＝2。‎ ‎（I）求证：BD⊥PC；‎ ‎（II）求证：MN∥平面PDC；‎ ‎19、（本小题满分12分）‎ 已知各项均为正数的等比数列的首项＝2，为其前n项和，若成等差数列。‎ ‎ （Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）令，，记数列的前n项和为，若对于任意的，恒成立，求实数的取值范围。‎ ‎20、（本小题满分13分）‎ 已知椭圆C：过点（1，），且离心率。‎ ‎（I）求椭圆方程；‎ ‎（II）设点A是椭圆C的左顶点，P，Q为椭圆C上异于点A的两动点，若直线AP，AQ的斜率之积为－，问直线PQ是否恒过定点？若恒过定点，求出该点坐标；若不恒过定点，说明理由。‎ ‎21、（本小题满分14分）‎ 设函数 ‎（I）用含的式子表示b；‎ ‎（II）令F（x）＝，其图象上任意一点P处切线的斜率恒成立，求实数的取值范围；‎ ‎（III）若＝2，试求在区间上的最大值。‎ 高三年级下学期第一次月考 数学（文）试题答案