2017-2018学年天津市静海县第一中学高二4月学生学业能力调研测试数学（文）试题（无答案）（Word版）

2017-2018学年天津市静海县第一中学高二4月学生学业能力调研测试数学（文）试题（无答案）（Word版）

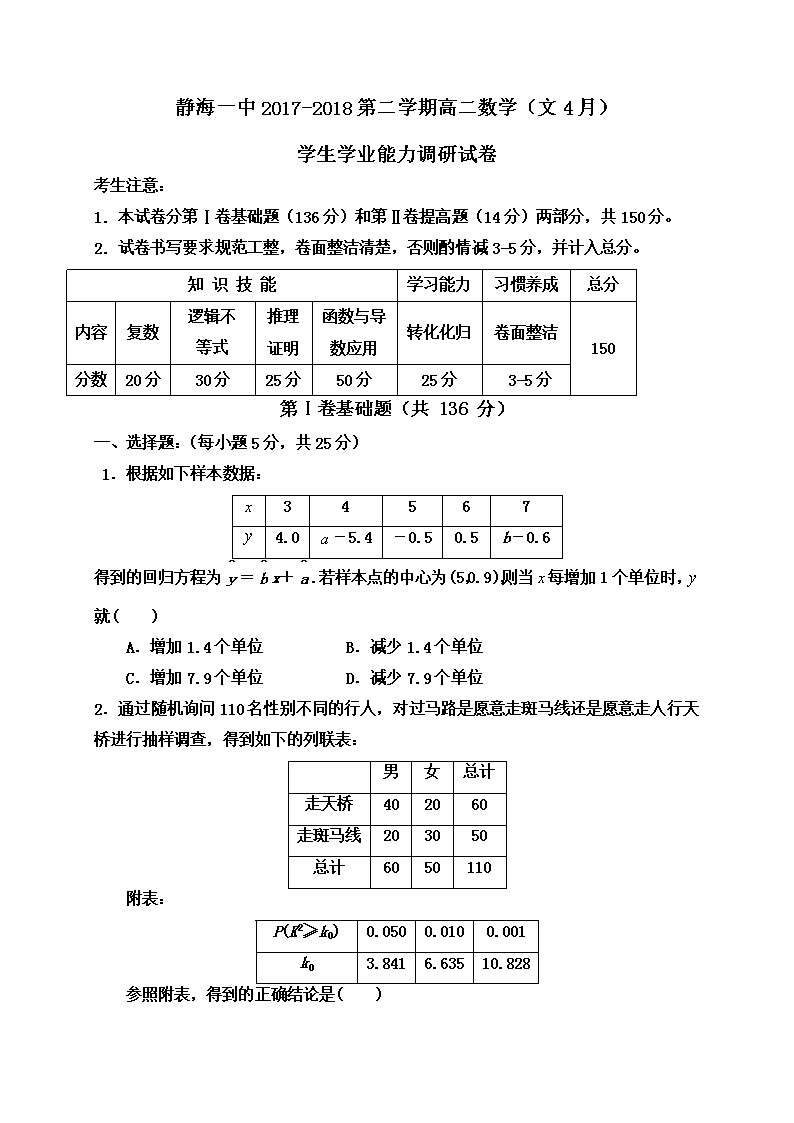
静海一中2017-2018第二学期高二数学（文4月）‎ 学生学业能力调研试卷 考生注意：‎ ‎1. 本试卷分第Ⅰ卷基础题（136分）和第Ⅱ卷提高题（14分）两部分，共150分。‎ ‎2. 试卷书写要求规范工整，卷面整洁清楚，否则酌情减3-5分，并计入总分。‎ 知 识 技 能 学习能力 习惯养成 总分 内容 复数 逻辑不 等式 推理证明 函数与导数应用 转化化归 卷面整洁 ‎150‎ 分数 ‎20分 ‎30分 ‎25分 ‎50分 ‎25分 ‎3-5分 第Ⅰ卷基础题（共 136 分）‎ 一、选择题：（每小题5分，共25分）‎ ‎ 1．根据如下样本数据：‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎4.0‎ ‎－5.4‎ ‎－0.5‎ ‎0.5‎ b－0.6‎ 得到的回归方程为＝x＋.若样本点的中心为(5，0.9)，则当每增加1个单位时，就(　　)‎ A．增加1.4个单位 B．减少1.4个单位 C．增加7.9个单位 D．减少7.9个单位 ‎2．通过随机询问110名性别不同的行人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如下的列联表：‎ 男 女 总计 走天桥 ‎40‎ ‎20‎ ‎60‎ 走斑马线 ‎20‎ ‎30‎ ‎50‎ 总计 ‎60‎ ‎50‎ ‎110‎ 附表：‎ P(K2≥k0)‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k0‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ 参照附表，得到的正确结论是(　　)‎ A．有99%以上的把握认为“选择过马路的方式与性别有关”‎ B．有99%以上的把握认为“选择过马路的方式与性别无关”‎ C．在犯错误的概率不超过0.1%的前提下，认为“选择过马路方式与性别有关”‎ D．在犯错误的概率不超过0.1%的前提下，认为“选择过马路方式与性别无关”‎ ‎3．给出下面类比推理命题(其中Q为有理数集，R为实数集，C为复数集)：‎ ‎①“若a，b∈R，则a－b＝0⇒a＝b”类比推出“若a，b∈C，‎ 则a－b＝0⇒a＝b”；‎ ‎②“若a，b，c，d∈R，则复数a＋bi＝c＋di⇒a＝c，b＝d”类比推出“若a，b，c，d∈Q，则a＋b＝c＋d⇒a＝c，b＝d”；‎ ‎③“若a，b∈R，则a－b>0⇒a>b”类比推出“若a，b∈C，则a－b>0⇒a>b”．其中类比结论正确的个数是(　　)‎ A．0 B．1 C．2 D．3‎ ‎4.若实数，满足，，则“”是“”的（ ）‎ A.充分不必要条件 B.必要不充分条件 ‎ C.充分必要条件 D.既不充分也不必要条件 ‎5．函数f(x)＝(x2－1)3＋2的极值点是(　　)‎ A.x＝1 B．x＝－‎1 ‎‎ C.x＝1或－1或0 D．x＝0‎ 二、填空题：（7题10分其余每题5分共35分）‎ ‎6. 已知命题p：∀x>0，总有(x＋1)ex>1，则非p 为______________‎ ‎7. 根据（）的图像，回答下列问题（每空2分）‎ ‎(1) 极大值为 ；‎ ‎(2)方程=0的实根为 ；‎ ‎(3)不等式的解集为 ；‎ ‎(4)函数的零点有 个；‎ ‎(5) 函数的零点个数就是方程的 个数，也是的图像与直线的交点个数.‎ ‎8．若复数z＝，其中i为虚数单位，则复数z的虚部是______________‎ ‎9.观察下列等式 ‎1＝1‎ ‎2＋3＋4＝9‎ ‎3＋4＋5＋6＋7＝25‎ ‎4＋5＋6＋7＋8＋9＋10＝49‎ ‎…‎ 照此规律，第n个等式为__________________‎ ‎10.函数在处取得极值是的 条件；‎ ‎11.已知三次函数在上单调递增，则的最小值为_________‎ 三、解答题：（共90分）‎ ‎12．（15分）实数m分别取什么数值时，复数z＝(m2＋‎5m＋6)＋(m2－‎2m－15)i ‎(1)与复数2－12i相等； (2)与复数12＋16i互为共轭复数；‎ ‎(3)对应的点在轴上方．‎ ‎13.（13分） 设函数。‎ ‎（1） 若曲线在点处的切线方程为，求的值；‎ ‎（2） 求函数的单调区间与极值。‎ ‎14.（30分）（规律总结题组）‎ ‎（1）若且，则的取值范围是________‎ ‎（2）．若，且，则的取值范围是________‎ ‎（3）已知,且,则的最小值是________. ‎ ‎（4）已知实数，若，且，则的最小值 ‎ ‎（5）已知实数，若，且则的最小值 __________ ‎ ‎15.（16分）已知函数（，为自然对数的底数）.‎ ‎（1）若曲线在点处的切线与直线垂直，求的单调区间；‎ ‎（2）若函数有两个极值点，求实数的取值范围；‎ 第Ⅱ卷 提高题（共16分）‎ ‎16.（16分）已知函数，，且曲线与在处有相同的切线.‎ ‎（1）求实数的值；‎ ‎（2）求证：在上恒成立；‎ ‎（3）当时，求方程在区间内实根的个数.‎ 静海一中2017-2018第二学期高二数学（文4月）‎ 学生学业能力调研试卷答题纸 试卷书写要求规范工整，卷面整洁清楚，否则酌情减3-5分，并计入总分。‎ 得分框 知识与技能 学法题 卷面 总分 第Ⅰ卷基础题（共134分）‎ 二、填空题（共35分）‎ ‎6._____ 7.（1） （2） （3） （4） （5） ‎ ‎8._______ 9. 10. 11. _ ‎ 三、解答题（本大题共5题，共90分） ‎ ‎12. （本题15分）‎ ‎13.（本题13分）‎ ‎（1） ‎ ‎（2）‎ ‎14.（本题30分）‎ ‎（1）‎ ‎（2）‎ ‎（3）‎ ‎（4）‎ ‎（5）‎ ‎15.（本题16分）‎ 第Ⅱ卷 提高题（共16分）‎ ‎16.（本题16分）‎ ‎ ‎