数学（文）卷·2018届广东省六校（珠海一中，中山纪念中学等）高三下学期第三次联考（2018

数学（文）卷·2018届广东省六校（珠海一中，中山纪念中学等）高三下学期第三次联考（2018

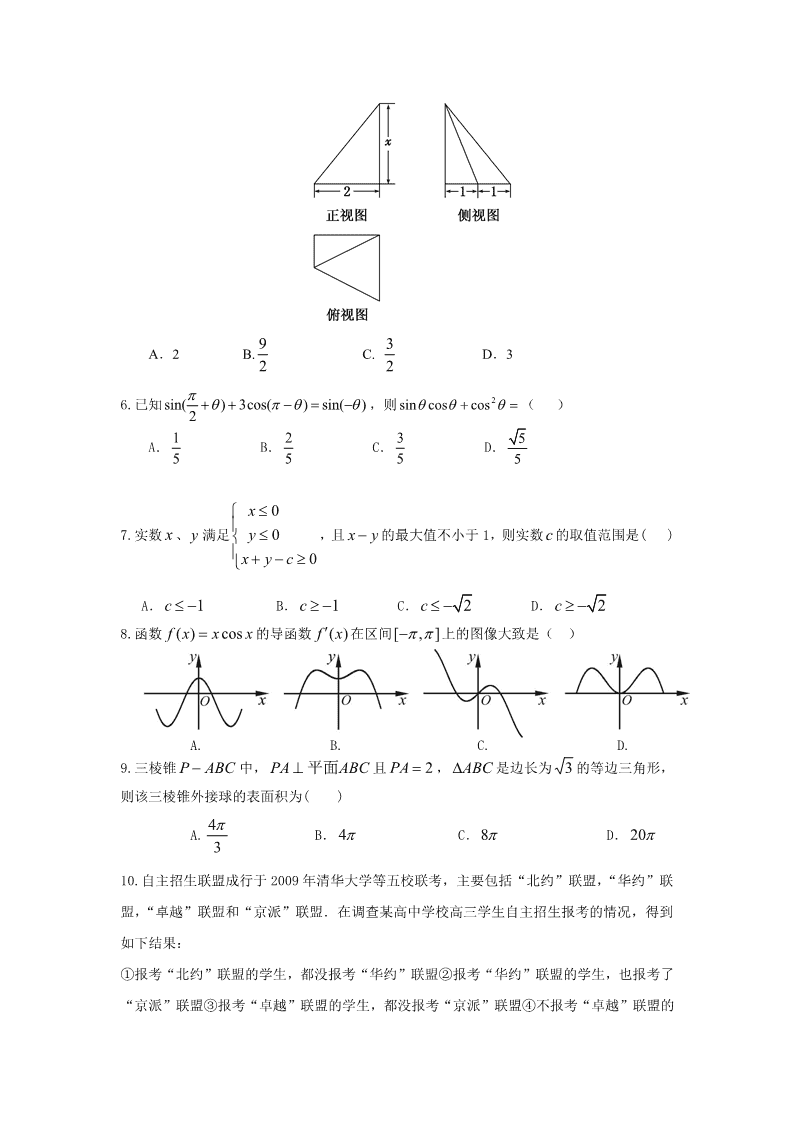
绝密★启用前 2018 届广东省六校第三次联考 文科数学 注意事项： 1．答题前，考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写 在答题卡上。 2．作答选择题时，选出每个小题答案后，用 2B 铅笔把答题卡上对应题目的答案信息点 涂黑。如需改动，用橡皮擦干净后，再选涂其它答案，写在本试卷上无效。 3．非选择题必须用黑色字迹签字笔作答，答案必须写在答题卡各题指定的位置上。 4．考试结束后，将本试卷和答题卡一并交回。 一、选择题：本题共 12 小题，每小题 5 分，共 60 分. 在每题给出的四个选项中，只有一项 符合题目要求. 1.函数 1( ) ln( 1) 2 f x x x     的定义域为（ ） A． (2 , )  B． ( 1 , 2) (2, )   C． ( 1 , 2) D． 1,2 2.如果复数 i bi 21 2   (其中 i 为虚数单位， b 为实数)的实部和虚部互为相反数，那么 b 等于 ( ) A． 6 B． 3 2 C． 3 2 D．2 3.高考结束后，同学聚会上，某同学从《爱你一万年》，《非你莫属》，《两只老虎》，《单身情 歌》四首歌中选出两首歌进行表演，则《爱你一万年》未选取的概率为（ ） A． 1 3 B． 1 2 C． 2 3 D． 5 6 4.圆 2 2( 2) 4x y   关于直线 3 3y x 对称的圆的方程是（ ） A． 2 2( 3) ( 1) 4x y    B． 2 2( 2) ( 2) 4x y    C． 2 2( 2) 4x y   D． 2 2( 1) ( 3) 4x y    5．某几何体的三视图如图所示，且该几何体的体积是 3，则正视图中的 x 的值是( ) A．2 B. 2 9 C. 2 3 D．3 6.已知 sin( ) 3cos( ) sin( )2          ，则 2sin cos cos    （ ） A． 1 5 B． 2 5 C． 3 5 D． 5 5 7.实数 x 、y 满足 0 0 0 x y x y c        ，且 x y 的最大值不小于 1，则实数 c 的取值范围是( ) A． 1c   B． 1c   C． 2c   D． 2c   8.函数 xxxf cos)(  的导函数 )(xf  在区间 ],[  上的图像大致是（ ） A. B. C. D. 9.三棱锥 ABCP  中， ABCPA 平面 且 2PA ， ABC 是边长为 3 的等边三角形， 则该三棱锥外接球的表面积为( ) A. 3 4 B． 4 C． 8 D． 20 10.自主招生联盟成行于 2009 年清华大学等五校联考，主要包括“北约”联盟，“华约”联 盟，“卓越”联盟和“京派”联盟．在调查某高中学校高三学生自主招生报考的情况，得到 如下结果： ①报考“北约”联盟的学生，都没报考“华约”联盟②报考“华约”联盟的学生，也报考了 “京派”联盟③报考“卓越”联盟的学生，都没报考“京派”联盟④不报考“卓越”联盟的 学生，就报考“华约”联盟 根据上述调查结果，下列结论错误的是（ ） A．没有同时报考“华约” 和“卓越”联盟的学生 B．报考“华约”和“京派”联盟的考生 一样多 C．报考“北约” 联盟的考生也报考了“卓越”联盟 D．报考“京派” 联盟的考生也报考 了“北约”联盟 11.设 1 2017 20162017 2016 20172016 , log , loga b c   ，则 , ,a b c 的大小关系为（ ） A． a b c  B． a c b  C. b a c  D． c b a  12. 已知双曲线 E ： 2 2 x a ﹣ 2 2 y b =1（ 0,0  ba ），点 F 为 E 的左焦点，点 P 为 E 上位于 第一象限内的点， P 关于原点的对称点为Q ，且满足 FQ3PF  ，若 bOP ，则 E 的离 心率为（ ） A. 2 B. 3 C. 2 D. 5 二．填空题：本题共4小题，每小题5分。 13.若向量 , 2, 2,( )a b a b a b a          满足 ，则向量 a 与 b  的夹角等 于 ． 14.执行如图所示的程序框图，则输出 S 的结果为 ． 15.已知函数 )(xfy  在点 ))2(,2( f 处的切线方程为 12  xy ，则函数 )()( 2 xfxxg  在点 ))2(,2( g 处的切线方程为________． 16．已知平面四边形 ABCD 为凸四边形（凸四边形即任取平面四边形一边所在直线， 其余各边均在此直线的同侧），且 2AB ， 4BC ， 5CD ， 3DA ， 则平面四边形 ABCD 面积的最大值为________． 三．解答题：共70分，解答应写出文字说明，证明过程或演算步骤。 （一）必考题：共60分。 17.（本小题满分 12 分） 已知数列 na 的前 n 项和为 nS ，且满足 22 nnSn  .( n N  ) 开始 0, 1S i  6?i  2i i  2S S i  S输出 结束 是 否 （1）求数列 na 的通项公式； （2）设 2 2 , ( 2 1) 2 , ( 2 )(1 )(1 ) na n n n n k b n ka a          （ k N  ），求数列 nb 的前 n2 项和 nT2 . 18.（本小题满分 12 分） 如图,在三棱柱 1 1 1ABC A B C 中，侧棱 1AA  底面 ABC , ,AB BC D 为 AC 的中点, 1 2A A AB  , 3BC  . (1)求证： 1 / /AB 平面 1BC D ； (2) 求四棱锥 1 1B AAC D 的体积. 19.（本小题满分 12 分） 随着社会的发展，终身学习成为必要，工人知识要更新，学习培训必不可少，现某 工厂有工人 1000 名，其中 250 名工人参加过短期培训（称为 A 类工人），另外 750 名工 人参加过长期培训（称为 B 类工人），从该工厂的工人中共抽查了 100 名工人，调查他 们的生产能力（此处生产能力指一天加工的零件数）得到 A 类工人生产能力的茎叶图（左 图），B 类工人生产能力的频率分布直方图（右图）. （1）问 A 类、B 类工人各抽查了多少工人，并求出直方图中的 x ; （2）求 A 类工人生产能力的中位数，并估计 B 类工人生产能力的平均数（同一组中的数 据用该组区间的中点值作代表）; （3) 若规定生产能力在[130，150]内为能力优秀，由以上统计数据在答题卡上完成下面 的 22 列联表，并判断是否可以在犯错误概率不超过 0.1%的前提下,认为生产能 力与培训时间长短有关. 能力与培训时间列联表 短期培训 长期培训 合计 能力优秀 能力不优秀 合计 参考数据： P(K2≥k) 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 2.072 2.706 3.841 5.024 6.635 7.879 10.828 参考公式： 2 2 ( ) ,( )( )( )( ) n ad bcK a b c d a c b d      其中 dcban  . 20.（本小题满分 12 分） 已知动点 M 到定点 )0,1(F 的距离比 M 到定直线 2x 的距离小 1. （1）求点 M 的轨迹C 的方程； （2）过点 F 任意作互相垂直的两条直线 21 ll 和 ，分别交曲线C 于点 BA, 和 NK, ．设线 段 AB ， KN 的中点分别为 QP, ，求证：直线 PQ 恒过一个定点. 21.（本小题满分 12 分） 已知函数    1ln122  xxaxxxf (其中 Ra ,且 a 为常数) ． （1）若对于任意的   ,1x ，都有   0xf 成立，求 a 的取值范围； （2）在（Ⅰ）的条件下，若方程   01 axf 在  2,0x 上有且只有一个实根， 求 a 的取值范围． （二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一 题计分。 22.（本题满分 10 分）[选修 4-4：坐标系与参数方程] 在直角坐标系 xOy 中，曲线 1C 的参数方程为        ty tx 5 42 5 32 （ t 为参数）．以坐标原点为 极点，以 x 轴正半轴为极轴建立极坐标系，曲线 2C 的极坐标方程为 cos tan   ． （1）求曲线 1C 的普通方程和曲线 2C 的直角坐标方程； （2）若 1C 与 2C 交于 A B, 两点，点 P 的极坐标为 π2 2, 4     ，求 1 1 | | | |PA PB  的值． 23.（本题满分 10 分）[选修 4-5：不等式选讲] 设函数 ( ) 2 2 1 ( 0)f x x a x a     ， ( ) 2g x x  ． （Ⅰ）当 1a  时，求不等式 ( ) ( )f x g x 的解集； （Ⅱ）若 ( ) ( )f x g x 恒成立，求实数 a 的取值范围． 2018 届广东省六校第三次联考 文科数学参考答案与评分标准 一．选择题：本大题共 12 小题，每小题 5 分。 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C C B D D C A A C D A B 二．填空题：本大题共 4 小题，每小题 5 分。 13． ； 14．30； 15． ；16． ； 16. 解：设 AC= ,在 中由余弦定理有 同理，在 中，由余弦定理有： ， 即 ①， 又 平 面 四 边 形 面 积 为 ， 即 ②. ①②平方相加得 ， 当 时， 取最大值 . 三、解答题 （本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演算步骤.） 17. (本小题满分 12 分) 解：（1）当 时， …2 分 （ ）， …………………………………3 分 当 时，由 得 ， …………………………………4 分 显然当 时上式也适合， ∴ …………………………………5 分 （2）∵ …………………………………6 分 ∴ …………………………………7 分 …………………9 分 …………………………………11 分 …………………………………12 分 18. (本小题满分 12 分) 解：（1）证明:连接 ,设 与 相交于点 , 连接 , ∵ 四边形 是平行四边形, ∴点 为 的中点. ∵ 为 的中点，∴ 为△ 的中位线, ∴ . ……………………… 2 分 ∵ 平面 , 平面 , ∴ 平面 . ……………………………………4 分 (2)解法 1: ∵ 平面 , 平面 , ∴ 平面 平面 ，且平面 平面 . 作 ，垂足为 ，则 平面 ， …………… 6 分 ∵ ， ， 在 Rt△ 中， ， ，…8 分 ∴四棱锥 的体积 …… 10 分 . ∴四棱锥 的体积为 . …… 12 分 解法 2: ∵ 平面 , 平面 ,∴ . ∵ ,∴ . ∵ , ∴ 平面 . …… 6 分 取 的中点 ,连接 ,则 ,∴ 平面 . 三棱柱 的体积为 , …… 8 分 则 , . …… 10 分 而 , ∴ . ∴ . ∴四棱锥 的体积为 . …… 12 分 19(本小题满分 12 分） 解：（1）由茎叶图知 A 类工人中抽查人数为 25 名, …………………………………1 分 ∴B 类工人中应抽查 100-25=75（名）. ………………………………………………2 分 由频率分布直方图得 (0.008+0.02+0.048+x)´10=1，得 x=0.024. …………………… 3 分 （2）由茎叶图知 A 类工人生产能力的中位数为 122 ………………………………4 分 由（1）及频率分布直方图，估计 B 类工人生产能力的平均数为 115´0.008´10+125´0.020´10+135´0.048´10+145´0.024´10=133.8 ………… …6 分 （3）由（1）及所给数据得能力与培训的 2´2 列联表， 短期培训 长期培训 合计 能力优秀 8 54 62 能力不优秀 17 21 38 合计 25 75 100 … … … … 9 分 由上表得 ＞10.828 ……11 分 因此,可以在犯错误概率不超过 0.1%的前提下,认为生产能力与培训时间长短有关. ………12 分 20. (本小题满分 12 分) 解：(1)由题意可知：动点 到定点 的距离等于 到定直线 的距离，根据 抛物线的定义可知，点 的轨迹 是抛物线。 ……2 分 ， 抛物线方程为： ……3 分 （2）设 两点坐标分别为 ，则点 的坐标为 ． 由题意可设直线 的方程为 ， 由 得 . .…………………5 分 因为直线 与曲线 于 两点，所以 ，． 所以点 的坐标为 .…………………6 分 由题知，直线 的斜率为 ，同理可得点 的坐标为 .………………… 7 分 当 时，有 ，此时直线 的斜率 .……8 分 所以，直线 的方程为 ， 整理得 . …………………10 分 于是，直线 恒过定点 ； 当 时，直线 的方程为 ，也过点 ． 综上所述，直线 恒过定点 ． …………………12 分 21(本小题满分 12 分） 解（1） …………… …1 分 当 时, 对于 恒成立, 在 上单调递增 ,此时命题成立;………………………… …3 分 当 时, 在 上单调递减,在 上单调递增, 当 时,有 .这与题设矛盾. 故 的取值范围是 ……………………………………………………5 分 （2）依题意 ,设 , 原题即为若 在 上有且只有一个零点,求 的取值范围. 显然函数 与 的单调性是一致的.  当 时,因为函数 在区间 上递减, 上递增, 所以 在 上的最小值为 , 由于 ,要使 在 上有且只有一个零点, 需满足 或 ,解得 或 ;………………………… …7 分 ‚当 时,因为函数 在 上单调递增, 且 , 所以此时 在 上有且只有一个零点;………………………… …9 分 ƒ当 时,因为函数 在 上单调递增,在 上单调递减,在 上单调递 增, 又因为 ,所以当 时,总有 , , 所以 在 上必有零点,又因为 在 上单调递增, 从而当 时, 在 上有且只有一个零点.………………………… …11 分 综上所述,当 或 或 时, 方程 在 上有且只有一个实根. …………………… …12 分 22．（本小题满分 10 分） 解：（1）曲线 的普通方程为 2 分 曲线 的直角坐标方程为: . 4 分 （2） 的参数方程的标准形式为 为参数)代入 得 6 分 设 是 对应的参数,则 7 分 10 分 23（本小题满分 10 分） 解：（1）当 时， 所以 或 或 ………………………3 分 解得 或 或 ……………………………………4 分 综上，不等式的解集为 .……………………………………………5 分 （2） ，转化为 令 ，……………………………………6 分 ，……………………………………7 分 时， ,……………………………………………8 分 令 得 ………………………………………………10 分