2017-2018学年云南省玉溪市玉溪一中高二上学期期末考试数学（理）试题 Word版

2017-2018学年云南省玉溪市玉溪一中高二上学期期末考试数学（理）试题 Word版

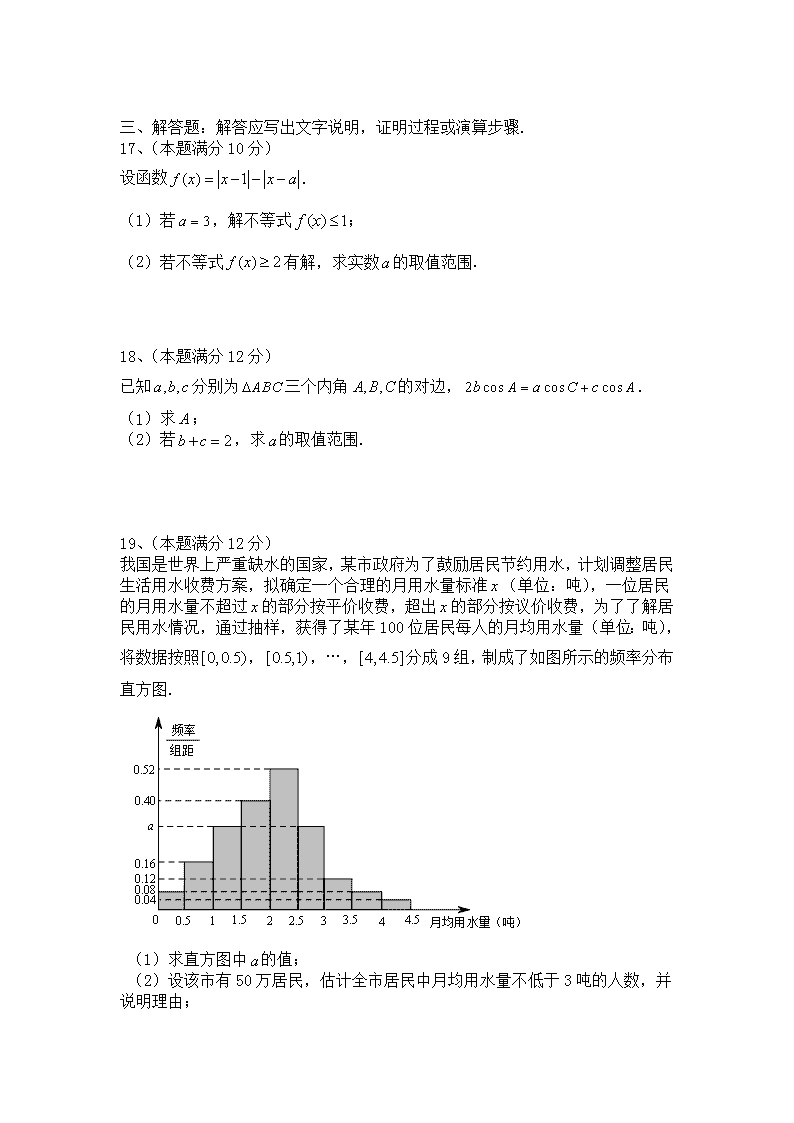
玉溪一中 2017—2018 学年上学期高二年级期末考 理科数学试卷 命题人：飞超 一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有 一项是符合题目要求的. 1、已知全集 ，集合 ，集合 ，则 ( ) A． B． C． D． 2、在等差数列 中，若 ， ，则 　　　　( ) A． B．0 C．1 D．6 3、抛物线 的准线方程是( ) A． B． C． D． 4、已知直线 分别在两个不同的平面 内，则“ ”是“平面 平面 ”的( ) A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 5、若 满足 则 的最大值为( ) A． B． C．5 D．9 6、函数 的零点所在的区间是( ) A． B． C． D． 7、函数 的部分图像如图所示，则 的单调递 减区间为( ) A． B． C． { }1,2,3,4,5,6,7,8U = { }2,3,5,6A = { }1,3,4,6,7B = UA B = { }2,5 { }3,6 { }2,5,6 { }2,3,5,6,8 { }na 2 4a = 4 2a = 6a = 1− 2 1 8x y= − 2x = − 2x = 1 32y = 1 32y = − ,a b ,α β //a b //α β ,x y 3 2 x x y y x ≤  + ≥  ≤ ， ， ， 2x y− 3− 1− 1( ) ( )4 xf x x= − ( 1,0)− 1(0, )4 1 1( , )4 2 1( ,1)2 ( ) cos( )f x xω ϕ= + ( ) cos( )f x xω ϕ= + 3(2 ,2 )4 4k k π ππ π− + k Z∈ 1 3( , )4 4k k− + k Z∈ 3 7(2 ,2 )4 4k k+ + k Z∈ D． 8、某三棱锥的三视图如右图所示，则该三棱锥的体积 为( ) A． B． C． D．1 9、双曲线 的左右焦点分别 为 ，点 在 上， 为等腰直角三角形，则双曲线的离心率为( ) A． B． C． D． 10、要得到函数 的图像，只需将函数 的图像( ) A．先向右平移 个单位，再关于 轴对称 B．先向左平移 个单位，再关于 轴对称 C．先关于 轴对称，再向右平移 个单位 D．先关于 轴对称，再向左平移 个单位 11、平行四边形 中， ， .若点 满足 ， ，则 ( ) A．20 B．15 C．9 D．6 12、若一个四棱锥的底面为正方形，顶点在底面的射影为正方形的中心，且该四 棱锥的体积为 9，当其外接球表面积最小时，它的高是( ) A． B．3 C． D． 二、填空题：本大题共 4 小题，每小题 5 分. 13、5 本不同的语文书，4 本不同的数学书，从中任意取 出 2 本，取出的书恰好都是数学书的概率为 . 14、执行右边的程序框图，若输入的 的值分别为 0 和 15，则输出的 的值为________. 15、曲线 在点 处的切线方程为 . 16、已知函数函数 ， ， ， ，使得 ，则实数 的 取值范围是 . 1 6 1 3 1 2 1 3(2 ,2 )4 4k k− + k Z∈ 2 2 2 2: 1x yC a b − = ( 0, 0)a b> > 1 2,F F P C 1 2PF F∆ 2 1− 2 1+ 3 3 1+ 3log (1 )y x= − 3logy x= 1 x 1 x y 1 y 1 ABCD 6AB = 4AD = ,M N 3BM MC=  2DN NC=  AM NM =   2 2 2 3 3 3 ,a b i 3 2xy e−= + (0,3) ln( ) xf x x = 3 21 1( ) 3 2g x x x m= − + 1 (0,3]x∀ ∈ 2 [ 1,2]x∃ ∈ − 1 2( ) ( )f x g x< m 三、解答题：解答应写出文字说明，证明过程或演算步骤. 17、（本题满分 10 分） 设函数 . （1）若 ，解不等式 ； （2）若不等式 有解，求实数 的取值范围. 18、（本题满分 12 分） 已知 分别为 三个内角 的对边， . （1）求 ； （2）若 ，求 的取值范围. 19、（本题满分 12 分） 我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民 生活用水收费方案，拟确定一个合理的月用水量标准 （单位：吨），一位居民 的月用水量不超过 的部分按平价收费，超出 的部分按议价收费，为了了解居 民用水情况，通过抽样，获得了某年 100 位居民每人的月均用水量（单位：吨）， 将数据按照 ， ，…， 分成 9 组，制成了如图所示的频率分布 直方图. （1）求直方图中 的值； （2）设该市有 50 万居民，估计全市居民中月均用水量不低于 3 吨的人数，并 说明理由； a 0.52 0.40 0.16 0.12 0.08 0.04 4.543.532.521.510.50 月均用水量（吨） 组距 频率 ( ) 1f x x x a= − − − 3a = ( ) 1f x ≤ ( ) 2f x ≥ a , ,a b c ABC∆ , ,A B C 2 cos cos cosb A a C c A= + A 2b c+ = a x x x [0,0.5) [0.5,1) [4,4.5] a （3）若该市政府希望使 的居民每月的用水量不超过标准 （吨），估计 的值，并说明理由.（结果保留到小数点后三位） 20、（本题满分 12 分） 如图,在以 为顶点的五面体中,面 为正方形, ， , ,且二面角 与二面角 都是 ． （1）证明：平面 平面 ； （2）求直线 与平面 所成角的正弦值． 21、（本题满分 12 分） 数列 的前 项和记为 ， ，点 在直线 上， . （1）当实数 为何值时，数列 是等比数列； （2）在（1）的结论下，设 ，求数列 的前 项和 . 22、（本题满分 12 分） 已知椭圆 的离心率为 ， ， ， ， 的面积为 1. （1）求椭圆 的方程； （2）设 的椭圆 上一点，直线 与 轴交于点 ，直线 与 轴交于点 ， 求证： 为定值. y x 80% x x , , , , ,A B C D E F ABEF //CD EF 2AF FD= 90AFD∠ =  D AF E− − C BE F− − 60 ABEF ⊥ EFDC BD BCE { }na n nS 1a t= 1( , )n nS a + 2 1y x= + *n N∈ t { }na 3 2 3 2 2 1 log logn n n b a a + =  { }nb n nT 2 2 2 2: 1x yC a b + = ( 0)a b> > 3 2 ( ,0)A a (0, )B b (0,0)O OAB∆ C P C PA M PB N AN BM 玉溪一中 2017—2018 学年上学期高二年级期末考 理科数学试卷参考答案 一、选择题：ABCD CCDA BCCB 二、填空题： 13、 . 14、4. 15、 . 16、 . 三、解答题： 17、解：（1） , ,......2 分 所以 或 或 解得 或 或 ......4 分 综上所述，不等式的解集为 .....5 分 （2） ，所以 ，.....8 分 解得 或 ，所以实数 的取值范围是 .....10 分 18、解：（1）由正弦定理可得： ，.....4 分 ， ，所以 ，即 ，因为 ，所以 ..6 分 （2） ， 所以 ，.8 分 因为 （当且仅当 时取等号）....10 分，所以 ， 解得 ，又因为 ，所以 的取值范围是 ....12 分 19、解：（1）由频率分布直方图知，月均用水量在 中的频率为 1 6 3 3 0x y+ − = 1 2( , )3e − +∞ 3a = 2 1 ( ) 1 3 2 4 1 3 2 3 x f x x x x x x − ≤ = − − − = − < <  ≥ 1 2 1 x ≤ − ≤ 1 3 2 4 1 x x < <  − ≤ 3 2 1 x ≥  ≤ 1x ≤ 51 2x< ≤ x∈∅ 5( , ]2 −∞ ( ) ( )( ) 1 1 1f x x x a x x a a= − − − ≤ − − − = − max( ) 1 2f x a= − ≥ 1a ≤ − 3a ≥ a ( , 1] [3, )−∞ − ∪ +∞ 2sin cos sin cos sin cos sin( ) sinB A A C C A A C B= + = + = (0, )B π∈ sin 0B ≠ 2cos 1A = 1cos 2A = (0, )A π∈ 3A π= 2 2 2 2 2 2( ) 2 4 2 1cos 2 2 2 2 b c a b c bc a bc aA bc bc bc + − + − − − −= = = = 24 3a bc− = 2( ) 12 b cbc +≤ = 1b c= = 24 3a− ≤ 1a ≥ 2a b c< + = a [1,2) [0,0.5) 0.08×0.5=0.04， 同理，在 ， ， ， ， ， ， ， 中的频率分别为 0.08，0.5×a ,0.20，0.26，0.5×a ,0.06，0.04，0.02．由 0.04+0.08+0.5×a+0.20+0.26+0.5×a+0.06+0.04+0.02=1，解得 a=0.30．.....4 分 （2）由（1），100 位居民每人月均用水量不低于 3 吨的频率为 0.06+0.04+0.02=0.12． 由以上样本的频率分布，可以估计全市 50 万居民中月均用水量不低于 3 吨的人 数为 50 万×0.12=6 万．.....8 分 （3）因为前 6 组的频率之和为 0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.80， 而前 5 组的频率之和为 0.04+0.08+0.15+0.20+0.26=0.73<0.80， 所以 2.5≤x<3．由 0.3×(x–2.5)=0.80–0.73，解得 ．所以，估计月 用水量标准为 吨时，80%的居民每月的用水量不超过标准．.....12 分 20、解（1）由已知可得 , , ，所以 平面 ．又 平面 ,故平面 平面 ．.....4 分 （2）过 作 ,垂足为 ,由（1）知 平面 ． 以 为坐标原点, 的方向为 轴正方向, 为单位长度,建立如图所示的空 间直角坐标系 ．.....5 分 由（1）知 为二面角 的平面角,故 ,则 , , ，可得 , , ． .....7 分 由 ,可得 平面 ,所以 为二 面角 的平面角, ．又因为 ，所以四边形 为等腰梯形，可求得 ， 从而可得 ， , ．设 是平面 的法向量,则 ,即 ,所以可取 ．.....10 分 设直线 与平面 所成角为 ，则 [0.5,1) [1,1.5) [1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5] 2.733x ≈ 2.733 F DFΑ ⊥ F FΑ ⊥ Ε FDF F∩ Ε = FΑ ⊥ FDCΕ FΑ ⊂ FΑΒΕ FΑΒΕ ⊥ FDCΕ D DG F⊥ Ε G DG ⊥ FΑΒΕ G GF x GF G xyz− DF∠ Ε D F− Α − Ε DF 60∠ Ε =  DF 2= DG 3= 4AF = ( )3,4,0Β − ( )3,0,0Ε − ( )D 0,0, 3 ( )3, 4, 3DΒ = − // FΒΕ Α ΒΕ ⊥ FDCΕ C F∠ Ε C F− ΒΕ − C F 60∠ Ε =  //CD EF CDFE 2CD = ( )C 2,0, 3− ( )C 1,0, 3Ε = ( )0,4,0ΕΒ = ( ), ,n x y z= CΒ Ε C 0 0 n n  ⋅Ε = ⋅ΕΒ =   3 0 4 0 x z y  + = = ( )3,0, 3n = − BD BCE θ 所以直线 与平面 所成角的正弦值为 .....12 分 21、解：（1） ① ② 当 时，①— ②可得 ，化简得 ， 所以 从第二项起 是等比数列......4 分 ， ，因为数列 是等比数列，所 以 ， ， .....6 分 （2）由（1）可知： 是首项为 1，公比为 3 的等比数列，所以 ，.....8 分 ，.....9 分 ..12 分 22、解：（1） ， 的面积为 1，即 ，椭圆中 列方 程求解得 ，所以椭圆 的方程为 ......4 分 （2）由（1）知， ，设 ，则 ......5 分 i）当 时，直线 的方程为 .令 ，得 . 从 而 .......7 分 直线 的方程为 .令 ，得 .从而 3 2 c a = OAB∆ 1 12 ab = 2 2 2a b c= + C 14 2 2 =+ yx )1,0(),0,2( BA ),( 00 yxP 44 2 0 2 0 =+ yx 00 ≠x PA )2(20 0 −−= xx yy 0=x 2 2 0 0 −−= x yyM 2 211 0 0 −+=−= x yyBM M PB 11 0 0 +−= xx yy 0=y 10 0 −−= y xxN 6 21sin cos , 1412 28 n BD n BD n BD θ ⋅ = = = =    BD BCE 21 14 1 2 1n na S+ = + *( )n N∈ 12 1n na S −= + ( 2)n ≥ 2n ≥ ! 12( ) 2n n n n na a S S a+ −− = − = 1 3( 2)n n a na + = ≥ { }na 1a t= 2 12 1 2 1a a t= + = + { }na 2 1 3a a = 2 1 3t t + = 1t = { }na 13n na −= 2 1 2 1 3 3 1 1 1 1 1( )log 3 log 3 (2 1)(2 1) 2 2 1 2 1n n nb n n n n− += = = −− + − + 1 2 1 1 1 1 1 1 1... [( ) ( ) ... ( )]2 1 3 3 5 2 1 2 1n nT b b b n n = + + + = − + − + + −− + 1 1(1 )2 2 1 2 1 n n n = − =+ + 2, 1, 3a b c= = = .......9 分 所以 .......11 分 ii）当 时， ， 所以 . 综上所述， 为定值 4. ......12 分 122 0 0 −+=−= y xxAN N 2 2112 0 0 0 0 −+⋅−+=⋅ x y y xBMAN 22 8844 22 48444 0000 0000 0000 0000 2 0 2 0 +−− +−−=+−− +−−++= yxyx yxyx yxyx yxyxyx 4= 00 =x 10 −=y ,2,2 == ANBM 4=⋅ BMAN BMAN ⋅ 2 0 0 0 0 (2 2 ) ( 1)( 2) y x y x − += − −