2018-2019学年安徽省定远重点中学高二下学期开学考试数学(文)试题 Word版
2018-2019学年安徽省定远重点中学高二下学期开学考试数学(文)试题
本试卷共150分,考试时间120分钟。
一、选择题(共12小题,每小题5分,共60分)
1.下列命题错误的是( )
A. 命题“若p,则q”与命题“若q,则p”互为逆否命题
B. 命题“∃x0∈R,x-x0>0”的否定是“∀x∈R,x2-x≤0”
C. ∀x>0且x≠1,都有x+>2
D. “若am2
1,条件q:x>a,且p是q的充分不必要条件,则a的取值范围是( )
A.a≥-1 B.a≤1 C.a≥1 D.a≤-3
3.命题“∃x0∈R,-2x0+1=0”的否定是( )
A. ∃x0∈R,-2x0+1≠0
B. 不存在x∈R,x3-2x+1≠0
C. ∀x∈R,x3-2x+1=0
D. ∀x∈R,x3-2x+1≠0
4.设AB是椭圆+=1(a>b>0)的长轴,若把线段AB分为100等份,过每个分点作AB的垂线,分别交椭圆的上半部分于点P1,P2,…,P99,F1为椭圆的左焦点,则|F1A|+|F1P1|+|F1P2|+…+|F1P99|+|F1B|的值是( )
A. 98a B. 99a C. 100a D. 101a
5.已知双曲线-=1(a>0,b>0),过其右焦点且垂直于实轴的直线与双曲线交于M、N两点,O是坐标原点.若OM⊥ON,则双曲线的离心率为( )
A. B. C.
D.
6.过抛物线y2=2px(p>0)的焦点作直线交抛物线于P(x1,y1),Q(x2,y2)两点,若x1+x2=3p,则|PQ|等于( )
A. 4p B. 5p C. 6p D. 8p
7.设f(x)、g(x)是定义在R上的恒大于0的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当af(b)g(b) B.f(x)g(a)>f(a)g(x)
C.f(x)g(b)>f(b)g(x) D.f(x)g(x)>f(a)g(a)
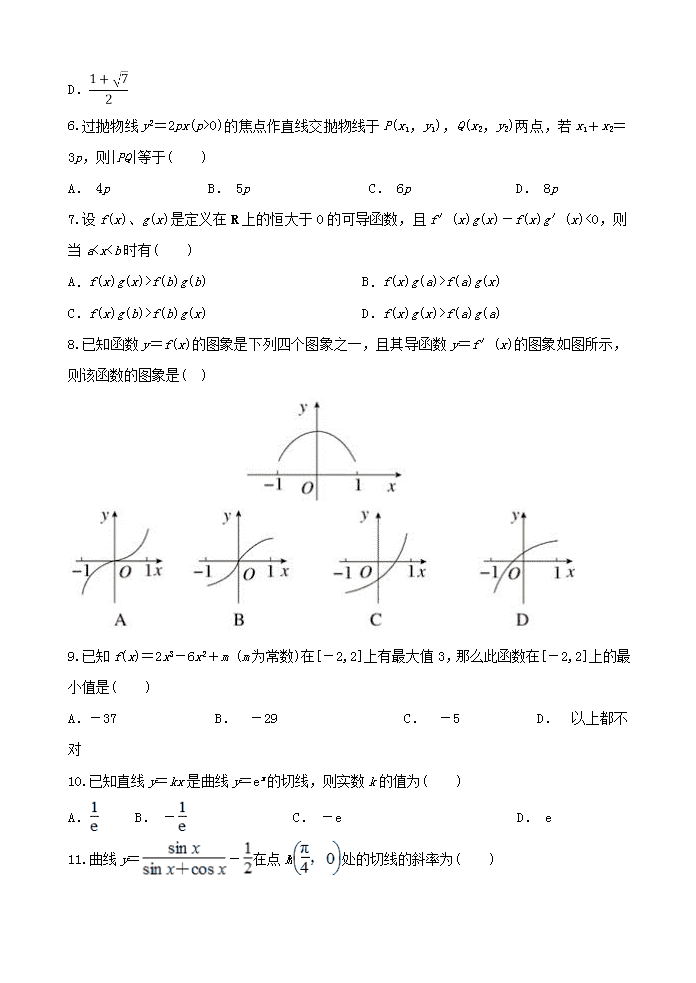
8.已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象是( )
9.已知f(x)=2x3-6x2+m (m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值是( )
A. -37 B. -29 C. -5 D. 以上都不对
10.已知直线y=kx是曲线y=ex的切线,则实数k的值为( )
A. B. - C. -e D. e
11.曲线y=-在点M处的切线的斜率为( )
A. - B. C. - D.
12.抛物线x2=2py(p>0)的焦点为F,其准线与双曲线-=1相交于A,B两点,若△ABF是等边三角形,则p等于( )
A. 6 B. 8 C. 4 D. 2
二、填空题(共4小题,每小题5分,共20分)
13.已知命题p:∃x0∈R,+2ax0+a≤0.若命题p是假命题,则实数a的取值范围是________.
14.如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是________.
15.过P(8,3)作双曲线9x2-16y2=144的弦AB,且P为弦AB的中点,那么直线AB的方程为________.
16.已知函数f(x)=x4+ax2-bx,且f′(0)=-13,f′(-1)=-27,则a+b等于________.
三、解答题(共6小题,共70分)
17.已知二次函数f(x)=ax2+x,试问是否存在实数a,使得命题“∃x0∈[0,1],f(x0)<1”是否成立,若存在,求出实数a的取值范围,否则说明理由.
18.如图所示,已知椭圆的两焦点为F1(-1,0),F2(1,0),P为椭圆上一点,且2|F1F2|=|PF1|+|PF2|.
(1)求此椭圆的方程;
(2)若点P在第二象限,∠F2F1P=120°,求△PF1F2的面积.
19.已知双曲线C:-=1(a>0,b>0)的离心率为,且过点(,1).
(1)求双曲线C的方程;
(2)若直线l:y=kx+与双曲线C恒有两个不同的交点A,B,求k的取值范围.
20.(1)求过曲线y=sinx上点P且与过这点的切线垂直的直线方程.
(2)已知点P(-1,1),点Q(2,4)是曲线y=x2上的两点,求与直线PQ平行的曲线y=x2的切线方程.
21.已知点F是抛物线C:y2=2px(p>0)的焦点,点M(0,)满足线段MF的中点在抛物线C上.
(1)求抛物线C的方程;
(2)若直线MF与抛物线C相交于A,B两点,求线段AB的长.
22.已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(2)当a2=4b时,求函数f(x)+g(x)的单调区间,并求其在区间(-∞,-1]上的最大值.
答案
1.D 2.C 3.D 4.D 5.C 6.A 7.C 8.B 9.A 10.D 11.B 12.A
13.(0,1)
14.
15. 3x-2y-18=0
16.18
17. 解:假设存在实数a,使得命题“∃x0∈[0,1],f(x0)<1”成立.
f(x)<1即为ax2+x<1,
当x=0时,0<1恒成立;
当x∈(0,1]时,a<=(-)2-,
由≥1,可得(-)2-≥0,
故a<0.
即存在实数a且a<0,
使得命题“∃x0∈[0,1],f(x0)<1”成立.
18. 解:
(1)由已知得c=1,|F1F2|=2,所以4=|PF1|+|PF2|=2a,所以a=2.
所以b2=a2-c2=4-1=3,
所以椭圆的方程为+=1.
(2)在△PF1F2中,|PF2|=2a-|PF1|=4-|PF1|.
由余弦定理得
|PF2|2=|PF1|2+|F1F2|2-2|PF1|·|F1F2|·cos 120°,
即(4-|PF1|)2=|PF1|2+4+2|PF1|,
所以|PF1|=.
所以=|F1F2|·|PF1|·sin 120°=×2××=.
19.解 (1)由e=,可得=,
所以a2=3b2,
故双曲线方程可化为-=1.
将点P(,1)代入双曲线C的方程,
解得b2=1,所以双曲线C的方程为-y2=1.
(2)联立直线与双曲线方程,
⇒(1-3k2)x2-6kx-9=0.
由题意得,
解得-10时,h(x)与h′(x)的情况如下:
所以函数h(x)的单调递增区间为和;单调递减区间为
.当-≥-1,即06时,函数h(x)在区间内单调递增,在区间内单调递减,在区间上单调递增.又因h-h(-1)=1-a+a2=(a-2)2>0,
所以h(x)在区间(-∞,-1)上的最大值为h=1.