- 2021-06-17 发布 |
- 37.5 KB |
- 8页

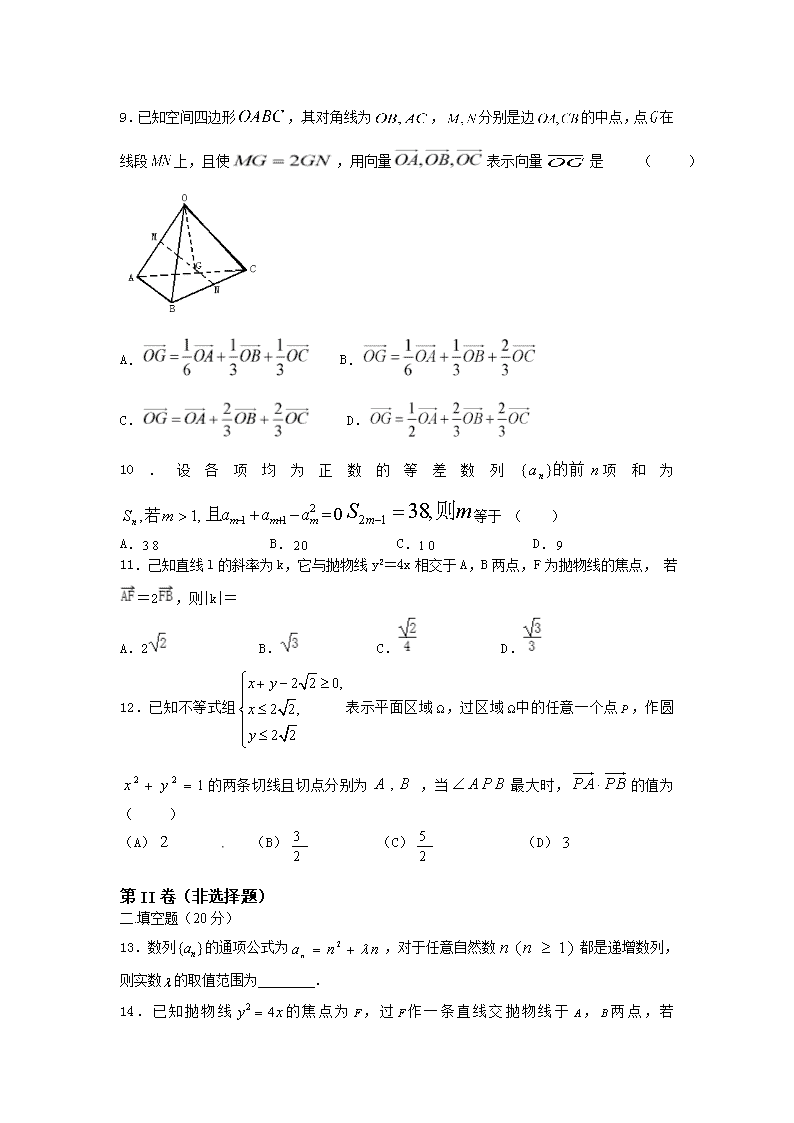

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2018届湖南省双峰县第一中学高二上学期第三次月考(2016-12)
双峰一中高二第三次月考试题 数学(理科) 考试时间:120分钟 总分:150分 第I卷(选择题) 一.选择题(60分) 1.“”是“方程的曲线是椭圆”的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.不充分不必要条件 2.已知向量,,且与互相垂直,则的值为( ) A. B. C. D.【来源:全,品…中&高*考+网】 3.已知A(2,-5,1),B(2,-2,4),C(1,-4,1),则与 的夹角为( ) A.30° B.45° C.60° D.90° 4.已知Sn是等差数列{an}的前n项和,若a7=9a3,则=( ) A.9 B.5 C. D. 5.若,则m、n的大小关系是( ) A. B. C. D. 6.下列命题中是真命题的是( ) ①“若,则不全为零”的否命题; ②“正多边形都相似”的逆命题; ③“若,则有实根”的逆否命题; ④“”的否定. A.①②③④ B.①③④ C.②③④ D.①④ 7.已知a,b,c是△ABC三边之长,若满足等式(a+b﹣c)( a+b+c)=ab,则∠C的大小为( ) A.60° B.90° C.120° D.150° 8.已知双曲线的离心率是,则的渐近线方程为 A. B. C. D. 9.已知空间四边形,其对角线为,分别是边的中点,点在线段上,且使,用向量表示向量是 ( ) 【来源:全,品…中&高*考+网】 A. B. C. D. 10.设各项均为正数的等差数列项和为等于 ( ) A. B. C. D. 11.己知直线l的斜率为k,它与抛物线y2=4x相交于A,B两点,F为抛物线的焦点, 若=2,则|k|= A.2 B. C. D. 12.已知不等式组表示平面区域,过区域中的任意一个点,作圆的两条切线且切点分别为,当最大时,的值为( ) (A) (B) (C) (D) 第II卷(非选择题) 二.填空题(20分) 13.数列的通项公式为,对于任意自然数都是递增数列,则实数的取值范围为 . 14.已知抛物线的焦点为,过作一条直线交抛物线于,两点,若 ,则 . 15.的内角所对的边分别为,且成等比数列,若,则的值为___________. 16.已知直线与椭圆相交于两点,且线段的中点在直线上,则此椭圆的离心率为_______ 三.解答题(10+12+12+12+12+12) 17.△ABC中内角A,B,C的对边分别为a,b,c,已知a=bcos C+csin B. (1)求B; (2)若b=2,求△ABC面积的最大值. 18.(本小题共13分) 数列{}中,,,且满足 (1)求数列{}的通项公式; (2)设,求. 19.某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示. 但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少? 20.给出两个命题: 命题甲:关于x的不等式x2+(a-1)x+a2≤0的解集为∅, 命题乙:函数y=(2a2-a)x为增函数.分别求出符合下列条件的实数a的范围. (1)甲、乙至少有一个是真命题; (2)甲、乙中有且只有一个是真命题. 21.平行四边形中,,,且,以BD为折线,把△ABD折起,,连接AC. B C A D B A C D (1)求证:; (2)求二面角B-AC-D的大小. 22.已知两点及,点在以、为焦点的椭圆上,且、、构成等差数列. (1)求椭圆的方程; (2)如图,动直线与椭圆有且仅有一个公共点,点是直线上的两点,且,. 求四边形面积的最大值. 参考答案【来源:全,品…中&高*考+网】 1B 2D 3C 4A 5A 6B 7C 8C 9A 10C 11A 12B 13. 14. 15. 16. 17.(1)B=(2)+1 (1)由已知及正弦定理,得 sin A=sin Bcos C+sin Csin B,① 又A=π-(B+C), 故sin A=sin(B+C)=sin Bcos C+cos Bsin C.② 由①,②和C∈(0,π)得sin B=cos B. 又B∈(0,π),所以B=………………………………………………………….5分 (2)△ABC的面积S=acsin B=ac. 由已知及余弦定理,得4=a2+c2-2accos. 又a2+c2≥2ac,故ac≤, 当且仅当a=c时,等号成立. 因此△ABC面积的最大值为+1………………………………..10分 18.(1) (2) 试题分析:解:(1)∴ ∴为常数列,∴{an}是以为首项的等差数列, 设,,∴,∴.…….6分 (2)∵,令,得. 当时,;当时,;当时,. ∴当时, ,. 当时,. ∴………………………………………..12分 19.该厂每天安排生产甲产品5吨,乙产品7吨,则该厂日产值最大,最大日产值为124万元. 设该厂每天安排生产甲产品x吨,乙产品y吨,则日产值, 线性约束条件为. 作出可行域. (6分) 把变形为一组平行直线系, 由图可知,当直线经过可行域上的点时,截距最大,即取最大值.解方程组,得交点 . 所以,该厂每天安排生产甲产品5吨,乙产品7吨,则该厂日产值最大,最大日产【来源:全,品…中&高*考+网】 值为124万元. (12分) 20.(1){a|a<-或a>};(2){a|查看更多
相关文章
- 当前文档收益归属上传用户