- 2021-06-17 发布 |
- 37.5 KB |
- 14页

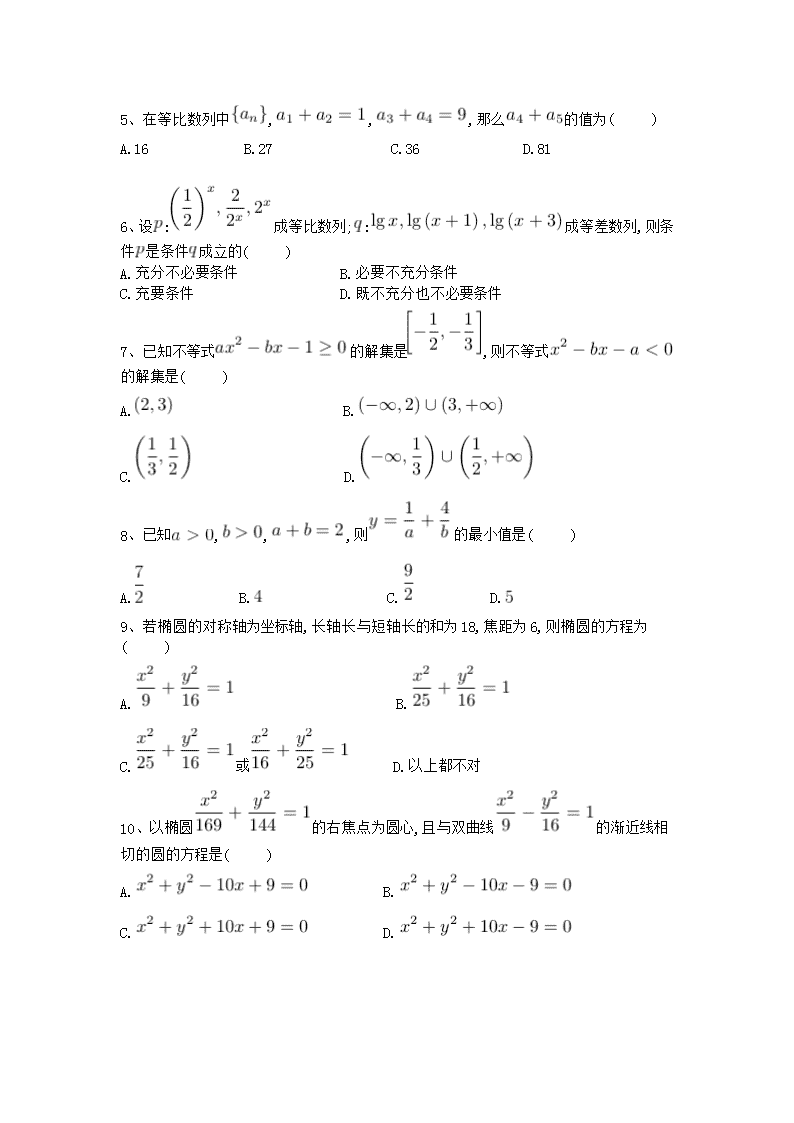

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2019届湖南省浏阳二中、五中、六中高二期中联考(2017-11)
2017年下学期高二年级二五六中期中联考数学理科试卷 时量:120分钟 总分:150分 姓名:___________班级:___________考号:___________ 注意事项:1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上 第1卷 评卷人 得分 一、选择题(本题共12个小题,每题5分,合计60分) 1、已知,命题“若,则”的否命题是( ) A.若,则 B.若,则 C.若,则 D.若,则 2、在中,角、、的对边分别为、、,若,则角的值为( ) A.. B. C.或 D.或 3、在中,,,且的面积为,则的长为( ) A. B. C. D. 4、等差数列中,若,,则的值是( ) A. 31 B.30 C.15 D.64 5、在等比数列中,,,那么的值为( ) A.16 B.27 C.36 D.81 6、设:成等比数列;:成等差数列,则条件是条件成立的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 7、已知不等式的解集是,则不等式的解集是( ) A. B. C. D. 8、已知,,,则的最小值是( ) A. B. C. D. 9、若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,焦距为6,则椭圆的方程为( ) A. B. C.或 D.以上都不对 10、以椭圆的右焦点为圆心,且与双曲线的渐近线相切的圆的方程是( ) A. B. C. D. 11、已知、为双曲线的左、右焦点,点在上,,则( ) A. B. C. D. 12、如图,在四边形中,,,,则该四边形的面积等于( ) A. B . C. D. 评卷人 得分 二、填空题(本题共4个小题,每题5分,合计20分) 13、已知变量满足约束条件,则的最大值为 . 14、 观察下列等式 ; ; ; ; … 照此规律,第个等式为 . 15、在中,角所对应的边分别为已知,则 . 16、下列四种说法: ①命题“,都有”的否定是“,使得”; ②若,,则是的必要不充分条件; ③把函数:的图象上所有的点向右平移个单位即可得到函数的图象; ④若向量,满足,,且与的夹角为,则. 其中正确的说法是 . 评卷人 得分 三、解答题(本题共6个小题,17题10,其余各题均为12分) 17、设有两个命题.命题:不等式的解集为;命题:函数在定义域内是增函数.如果为假命题,为真命题,求的取值范围. 18、在中,分别为内角的对边. (1)求角的大小; (2)若,试判断的形状. 19、设是等差数列,是各项都为正数的等比数列,且 (1)求数列的通项公式; (2)设数列的前项和为试比较与的大小. 20、围建一个面积为的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为 的进出口,如图所示,已知旧墙的维修费用为元/,新墙的造价为元/,设利用的旧墙的长度为,修建此矩形场地围墙的总费用为(元). (1)将表示为的函数; (2)试确定,使修建此矩形场地围墙的总费用最小,并求出最小总费用. 21、已知椭圆的一个顶点为,离心率为,直线与椭圆交于不同的两点,. (1)求椭圆的方程. (2)当的面积为时,求的值 22. 如图,已知抛物线焦点为,直线经过点且与抛物线相交于,两点 (1)若线段的中点在直线上,求直线的方程; (2)若线段,求直线的方程 2017年下学期高二年级二五六中期中联考数学理科试卷答案 一、选择题 1. 答案: A 解析: 根据四种命题的定义,命题“若,则”的否命题是“若,则“ 故选A. 2. 答案: B 解析: 因为所以由余弦定理,得,故选B. 3. 答案: A 解析: ∵,∴,∴,∴,∴,故选A. 4. 答案: C 解析: 由等差数列的通项公式,得,∴,∴,故选C 5. 答案: B 解析: 由等比数列的通项公式及性质知,∵,,∴,∴,故选B. 6. 答案: C 解析: 若成等比数列,则,解得. 若成等差数列,则,即,解得, 所以是的充要条件. 7. 答案: A 解析: 根据题意,由于不等式的解集是,则可知 ∴,那么可知不等式的解集为,故选A 点评:主要是考查了一元二次不等式的解集的求解,属于基础题。 8. 答案: C 解析: 依题意得. 当且仅当,即,时取等号,即的最小值是,选C. 9. 答案: C 解析: 由,,,,,得,,所以或,故选C. 10. 答案: A 解析: 由椭圆的方程得,根据椭圆的简单性质得:所以右焦点坐标为,即所求圆心坐标为. 由双曲线的方程得到,所以双曲线的渐近线方程为,即 ,由双曲线的渐近线与所求的圆相切,得到圆心到直线的距离,则所求圆的方程为:,即. 11. 答案: C 解析: 双曲线可化为,则,,,所以,由双曲线的定义可知,所以,在中,由余弦定理可得,故选C. 考点:1.双曲线的定义及其标准方程;2.余弦定理. 12. 答案: D 解析: 四边形的面积为与两部分的和,连接,由余弦定理知,∴,∴,∴.∴. 二、填空题 13. 答案: 11 解析: 先画出可行域(如下图中阴影部分)及直线,将直线平移到处时,取得最大值,于是得到. 14. 答案: 解析: 根据题意,由于观察下列等式 照此规律,等式左边的第一个数就是第几行的行数,那么共有个数相加,右边是最中间数的平方,故第个等式为. 15. 答案: 2 解析: 由已知条件及余弦定理,得,化简,得,则. 16. 答案: ①②④ 解析: ①正确,②若,则,当或为负数时,不成立.若,∴,∴,故②正确.③把的图象上所有的点向右平移个单位,得到,故③不正确.④由题可知,,∴,∴,故④正确. 三、解答题 17.(本题10分) 答案: 对于:因为不等式的解集为,所以. 解这个不等式,得. (3分) 对于:在定义域内是增函数, 则有所以. (5分) 又为假命题,为真命题,所以必是一真一假. 当真假时有, (7分) 当假真时有. (9分) 综上所述,的取值范围是. (10分) 18.(本题 12分) 答案: 1.由及正弦定理,得 , 即①则 (3分) , 又∵,∴ (6分) 2.由①,得,∴ (8分) 又②,∴③,由②③,得,∵, ∴,∴是等腰三角形。 (12分) 19. (本题 12分) 答案: 1.设的公差为,的公比为, 则依题意有,且 (3分) 解得, ∴,. (6分) 2., ,① (8分) ,② 由②-①得 (10分) , (12分) 20. (本题 12分) 答案: 1.设矩形的另一边长为, 则, (3分) 由已知,得, ∴. (6分) 2.∵, ∴, (8分) ∴, (10分) 当且仅当,即时,等号成立. ∴当时,修建围墙的总费用最小,最小总费用是元. (12分) 21. (本题 12分) 答案: 1.∵椭圆一个顶点为,离心率为, ∴解得 (3分) , ∴椭圆的方程为. (5分) 2.直线与椭圆联立,得 消元可得. 设,, 则,, (8分) ∴ ∵到直线的距离为. ∴的面积. (10分) ∵的面积为, ∴, ∴. (12分) 22. (1):解:由已知得交点坐标为, 设直线的斜率为,,,中点 则,, (3分) 所以,又,所以 故直线的方程是: (6分) (2) :解:设直线的方程为, 与抛物线方程联立得, (8分) 消元得, 所以有,, (10分) 所以有,解得, 所以直线的方程是:,即 (12分)查看更多