数学理卷·2018届青海省西宁二十一中高二6月月考（2017-06）

数学理卷·2018届青海省西宁二十一中高二6月月考（2017-06）

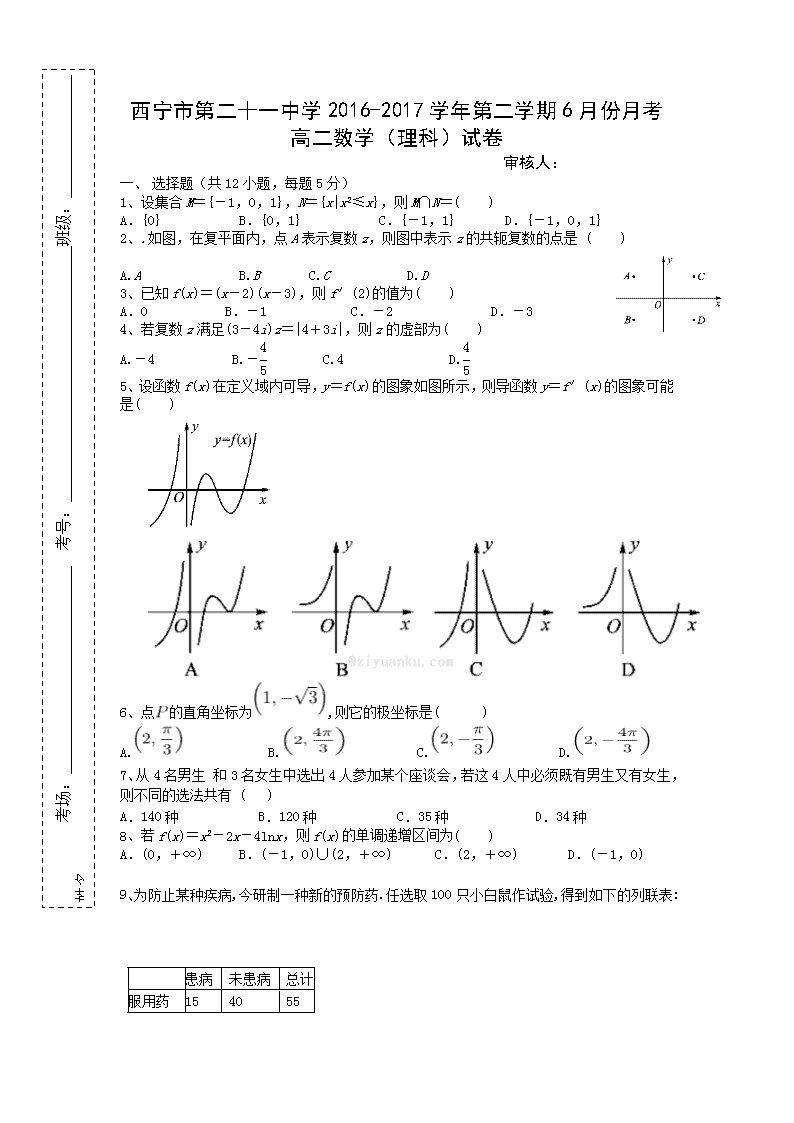
考场： 考号： 班级： 姓名： ‎ 西宁市第二十一中学2016-2017学年第二学期6月份月考 高二数学（理科）试卷 审核人：‎ 一、 选择题（共12小题，每题5分）‎ ‎1、设集合M＝{－1，0，1}，N＝{x|x2≤x}，则M∩N＝(　　)‎ A．{0} B．{0，1} C．{－1，1} D．{－1，0，1}‎ ‎2、.如图，在复平面内，点A表示复数z，则图中表示z的共轭复数的点是 (　　)‎ A.A B.B C.C D.D ‎3、已知f(x)＝(x－2)(x－3)，则f′(2)的值为(　　)‎ A．0 B．－1 C．－2 D．－3‎ ‎4、若复数z满足(3－4i)z＝|4＋3i|，则z的虚部为(　　)‎ A.－4 B.－ C.4 D. ‎5、设函数f(x)在定义域内可导，y＝f(x)的图象如图所示，则导函数y＝f′(x)的图象可能是(　　) ‎ ‎6、点的直角坐标为,则它的极坐标是(    ) A. B. C. D.‎ ‎7、从4名男生 和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法共有 (  )‎ A．140种 B．120种 C．35种 D．34种 ‎8、若f(x)＝x2－2x－4lnx，则f(x)的单调递增区间为(　　)‎ A．(0，＋∞) B．(－1，0)∪(2，＋∞) C．(2，＋∞) D．(－1，0)‎ ‎9、为防止某种疾病,今研制一种新的预防药.任选取100只小白鼠作试验,得到如下的列联表:‎ ‎ ‎ 患病 未患病 总计 服用药 ‎15‎ ‎40‎ ‎55‎ 没服用药 ‎20‎ ‎25‎ ‎45‎ 总计 ‎35‎ ‎65‎ ‎100‎ ‎,则在犯错误的概率不超过(  )的前提下认为“药物对防止某种疾病有效”。 A. 0.025      B.0.10       C. 0.01       D. 0.005 参考数据:‎ p(K2≥k0)‎ ‎ 0.50‎ ‎0.40‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎0.455‎ ‎0.708‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎10、函数f(x)＝x3－3x2＋m在区间[－1，1]上的最大值是2，则常数m＝(　　)‎ A．－2 B．0 C．2 D．4‎ ‎11、甲、乙两台自动车床生产同种标准件，表示甲机床生产1000件产品中的次品数，表示乙机床生产1000件产品中的次品数，经过一段时间的测试，与的分布列分别为：‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎0.7‎ ‎0.1‎ ‎0.1‎ ‎0.1‎ P ‎0.5‎ ‎0.3‎ ‎0.2‎ ‎0‎ 据此判定（ ）‎ A. 甲比乙质量好 B. 乙比甲质量好 C. 甲与乙质量相同 D. 无法判定 ‎12、对于上的可导函数,若且有,则必有(    )‎ A. B.‎ C. D.‎ 二、填空题（共4小题，每题5分）‎ ‎13、若曲线y＝e－x上点P处的切线平行于直线2x＋y＋1＝0，则点P的坐标是________．‎ ‎14、某电视台连续播放5个广告，其中有3个不同的商业广告和2个不同的公益广告，要求最后播放的必须是公益广告，且2个公益广告不能连续播放，则不同的播放方式有________种.(用数字作答)‎ ‎15、在的展开式中的常数项是 。‎ ‎16、一批产品的二等品率为，从这批产品中每次随机取一件，有放回地抽取次，表示抽到的二等品件数，则 ．‎ 选择题答题卡 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 三、解答题 ‎17（10分）设函数.（1）若的两个极值点为,,且,（1）求实数的值；（2）是否存在实数,使得是上的单调函数?若存在,求出的值;若不存在,说明理由.‎ ‎ ‎ ‎18（12分）4位学生与2位教师并坐合影留念，针对下列各种坐法，试问：各有多少种不同的坐法？（1）教师必须坐在中间；（2）教师不能坐在两端，且不能相邻。‎ ‎19（12分）甲、乙两队参加知识竞赛，每队3人，每人回答一个问题，答对者为本队赢得一分，答错得零分.假设甲队中每人答对的概率均为，乙队中3人答对的概率分别为，，，且各人回答正确与否相互之间没有影响.用X表示甲队的总得分.‎ ‎(1)求随机变量X的分布列和均值；‎ ‎(2)用A表示“甲、乙两个队总得分之和等于‎3”‎这一事件，用B表示“甲队总得分大于乙队总得分”这一事件，求P(AB).‎ ‎20（12分）抛掷一颗骰子两次，定义随机变量 ‎（1）试写出随机变量的分布列；‎ ‎（2）抛掷一颗骰子两次，在第一次掷得向上一面点数是偶数的条件下，求第二次掷得向上一面点数也是偶数的概率。‎ ‎21（12分）设f(x)＝a(x－5)2＋6lnx，其中a∈R，曲线y＝f(x)在点(1，f(1))处的切线斜率为2.‎ ‎(1)确定a的值；‎ ‎(2)求函数f(x)的单调区间与极值．‎ ‎22（12分）设函数 (1) 求曲线在点处的切线方程； （2）求函数的单调区间 ‎（3）若函数在区间内单调递增，求的取值范围。‎ 西宁市第二十一中学2016-2017学年第二学期6月份月考 高二数学（理科）试卷答案 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B B B D D C D C B C A C 二、填空题 ‎13、‎ ‎14、 36‎ ‎15、 7 ‎ ‎16、 1.96‎ 三、解答题 ‎17、解:（1）.由已知有, 从而∴.（2） 所以不存在实数,使得是上的单调函数。‎ ‎18、解：（1）先排2名教师在中间，然后排4名同学，所以共有不同的坐法（种）；（2）先排2名教师在中间4个位置但不相邻，然后排4名同学，所以共有不同的坐法 ‎19、解：(1)解法一：由题意知，X的可能取值为0，1，2，3，且 P(X＝0)＝C×＝，‎ P(X＝1)＝C××＝，‎ P(X＝2)＝C××＝，‎ P(X＝3)＝C×＝.‎ 所以X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P X的均值E(X)＝0×＋1×＋2×＋3×＝2.‎ 解法二：根据题设可知X～B，‎ 因此X的分布列为 P(X＝k)＝C×× ‎＝C×，k＝0，1，2，3.‎ 因为X～B，所以E(X)＝3×＝2.‎ ‎(2)用C表示“甲队得2分乙队得1分”这一事件，用D表示“甲队得3分乙队得0分”这一事件，所以AB＝C＋D，且C，D互斥，P(C)＝×(××＋××＋××)＝.‎ P(D)＝×＝，‎ 由互斥事件的概率公式得 P(AB)＝P(C)＋P(D)＝＋＝.‎ ‎20、解：（1）当第一次向上的面的点数等于第二次向上的面点数时，有6种情况，所以 ‎，由互斥事件概率公式得，‎ 所以所求分布列是 ‎1‎ ‎0‎ P ‎（2）设第一次掷得向上一面点数是偶数的事件为A，第二次掷得向上一面点数是偶数的事件为B，在第一次掷得向上一面点数是偶数的条件下，第二次掷得向上一面点数也是偶数的概率为：‎ ‎=或 ‎21、解：(1)f′(x)＝2a(x－5)＋，‎ 依题意，f′(1)＝6－8a＝2，得a＝.‎ ‎(2)由(1)知，f(x)＝(x－5)2＋6lnx(x＞0)，‎ f′(x)＝x－5＋＝.‎ 令f′(x)＝0，得x＝2或3.‎ x，f′(x)，f(x)的变化情况如下表：‎ x ‎(0，2)‎ ‎2‎ ‎(2，3)‎ ‎3‎ ‎(3，＋∞)‎ f′(x)‎ ‎＋‎ ‎0‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎ ‎↗‎ 极大值 ‎↘‎ 极小值 ‎↗‎ 故f(x)的单调增区间为(0，2)和(3，＋∞)，‎ 单调减区间为(2，3)．‎ f(x)的极大值f(2)＝＋6ln2，极小值f(3)＝2＋6ln3.‎ ‎22、‎ ‎【来源：全,品…中&高*考+网】‎