江西省山江湖协作体2019-2020学年高二上学期第三次月考数学（理）试题

江西省山江湖协作体2019-2020学年高二上学期第三次月考数学（理）试题

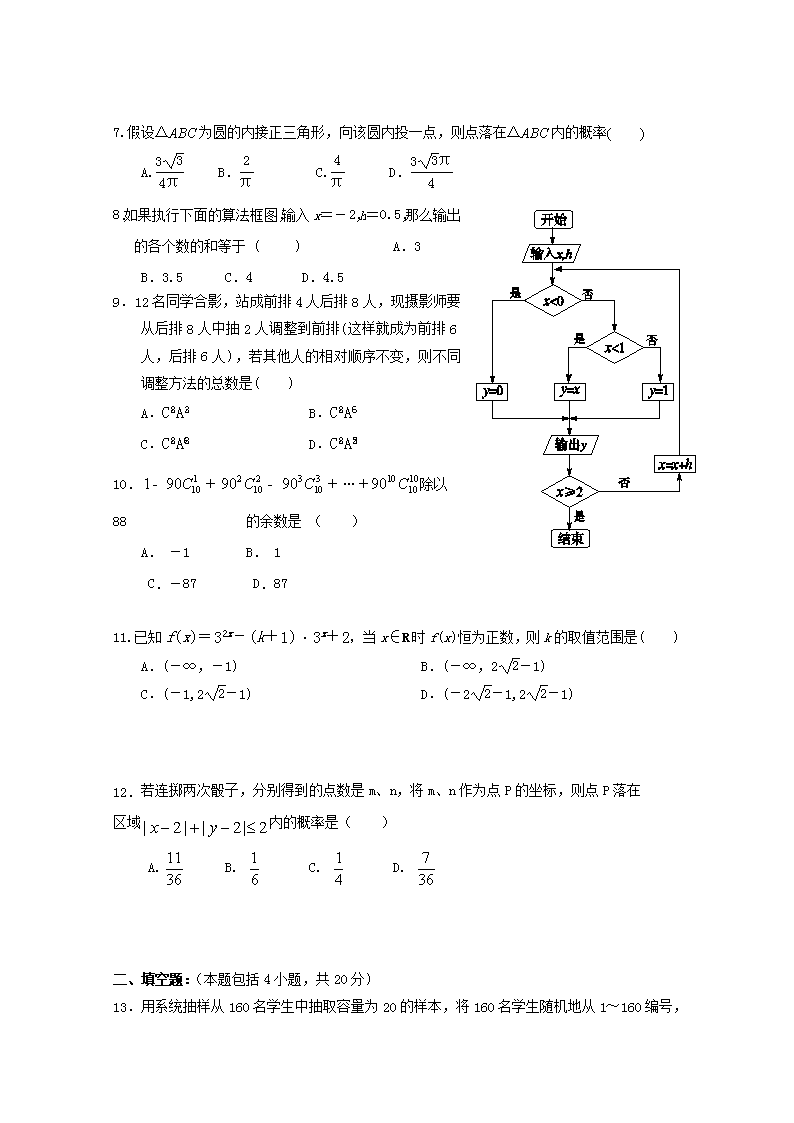
‎“山江湖”协作体高二年级第三次月考 数学（理科）试卷（统招班）‎ 一、选择题：（本题包括12小题，共60分，每小题只有一个选项符合题意）‎ ‎1．甲、乙两人计划从A，B，C三个景点中各选择两个游玩，则两人所选景点不全相同的选法共有(　　)‎ A．3种 B．6种 C．9种 D．12种 ‎2．某学院A，B，C三个专业共有1 200名学生，为了调查这些学生勤工俭学的情况，拟采用分层抽样的方法抽取一个容量为120的样本．已知该学院的A专业有380名学生，B专业有420名学生，则在该学院的C专业应抽取的学生人数为(　　)‎ A．30 B．40‎ C．50 D．60‎ ‎3.已知函数y=f(x)的图象如图1，则不等式＞0的解集为（ ）‎ A.（－∞,1） B.( －2,1)‎ C.( －∞, －2) D.( －∞, －2)∪(1,+∞) 图1‎ ‎4.已知，之间的一组数据：‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎1‎ ‎3‎ ‎5‎ ‎7‎ 则与的线性回归方程必过点 ( ) ‎ A．(2,2) B．(1.5,0) C．(1,2) D．(1.5,4) ‎ ‎5．某赛季，甲、乙两名篮球运动员都参加了11场比赛，他们所有比赛得分的情况用如右图所示的茎叶图表示，则甲、乙两名运动员得分的中位数分别为(　　)‎ A．19,13 B．13,19‎ C．20,18 D．18,20‎ ‎6．若(x－2)5＝a5x5＋a4x4＋a3x3＋a2x2＋a1x＋a0，则a1＋a3＋a5＝(　　)．‎ A．1 B．－1 ‎ C．121 D．106‎ ‎7.假设△ABC为圆的内接正三角形，向该圆内投一点，则点落在△ABC内的概率(　　)‎ A. B． C. D． ‎8．如果执行下面的算法框图，输入x＝－2，h＝0.5，那么输出的各个数的和等于 ( ) A．3 B．3.5 C．4 D．4.5‎ ‎9．12名同学合影，站成前排4人后排8人，现摄影师要从后排8人中抽2人调整到前排(这样就成为前排6人，后排6人)，若其他人的相对顺序不变，则不同调整方法的总数是(　　)‎ A．CA B．CA C．CA D．CA ‎10．…除以88 的余数是 （ ）‎ A． －1　　 B． 1　　 ‎ ‎ C．－87　　 D．87‎ ‎11.已知f(x)＝32x－(k＋1)·3x＋2，当x∈R时f(x)恒为正数，则k的取值范围是(　　)‎ A．(－∞，－1) B．(－∞，2－1)‎ C．(－1,2－1) D．(－2－1,2－1)‎ 12． 若连掷两次骰子，分别得到的点数是m、n，将m、n作为点P的坐标，则点P落在 区域内的概率是（　　）‎ ‎ A. B. C. D. ‎ 二、填空题：（本题包括4小题，共20分)‎ ‎13．用系统抽样从160名学生中抽取容量为20的样本，将160名学生随机地从1～160编号，按编号顺序平均分成20组(1～8号，9～16号，…，153～160号)，若第16组抽出的号码为126，则第1组中用抽签的方法确定的号码是 .‎ ‎14.已知实数x,y满足条件则目标函数z=2x－y的最大值是 .‎ ‎15.已知二次函数f(x)=ax2+2x+c(x∈R)的值域为［0,+∞),则的最小值为 .‎ ‎16．从0，1，2，3，4中每次取出不同的三个数字组成三位数，那么这些三位数的个位数之和为 .‎ 三．解答题：（本题包括6小题，共70分）‎ 17. ‎(本小题满分10分)已知x＞0,y＞0且2x+8y－xy=0,‎ 求：（1）xy的最小值；（2）x+y的最小值.‎ ‎18．(本小题满分12分)已知二项式(x－)10的展开式中，‎ ‎(1)求展开式中含x4项的系数；‎ ‎(2)如果第3r项和第r＋2项的二项式系数相等，试求r的值．‎ ‎19.(本小题满分12分)有7本不同的书：‎ （1） 全部分给6个人，每人至少一本，有多少种不同的分法？‎ ‎（2）全部分给5个人，每人至少一本，有多少种不同的分法？．‎ ‎20．(本小题满分12分)某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：第一组[13,14)；第二组[14,15)……第五组[17,18]．如图是按上述分组方法得到的频率分布直方图：‎ 图2‎ ‎(1)若成绩大于或等于14秒且小于16秒认为良好，求该班在这次百米测试中成绩良好的人数；‎ ‎(2)设m、n表示该班某两位同学的百米测试成绩，且已知m，n∈[13,14)∪[17,18]．求事件“|m－n|＞1”的概率．‎ ‎21.(本小题满分12分)设一元二次方程Ax2＋Bx＋C＝0，根据下列条件分别求解：‎ ‎(1)若A＝1，B、C是1枚骰子先后掷两次出现的点数，求方程有实数根的概率；‎ ‎(2)若B＝－A，C＝A－3，且方程有实数根，求方程至少有一个非正实数根的概率。‎ ‎22．(本小题满分12分)已知函数f(x)＝(a、b为常数)，且方程f(x)－x＋12＝0有两个实根为x1＝3，x2＝4.‎ ‎(1)求函数f(x)的解析式；‎ ‎(2)设k>1，解关于x的不等式f(x)< ‎“山江湖”协作体高二年级第三次月考 数学（理科）答案（统招班）‎ 一． 选择题（60分）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ B B B D A C A B C B B A 二．填空题（20分）‎ ‎13.6 14. 6 15．4 16. 90‎ 三．解答题（70分）‎ ‎17.（1）由2x+8y－xy=0,得+=1,又x＞0,y＞0，‎ 则1=+≥,得xy≥64.‎ 当且仅当,即时等号成立.‎ 此时=64.………(5分)‎ ‎(2)由2x+8y－xy=0,得+=1,‎ 则x+y= (x+y)=10++≥10+2=18.‎ 当且仅当即时等号成立.‎ 此时=18.………(10分)‎ ‎18.(1)设第k＋1项为Tk＋1‎ ‎＝Cx10－k(－)k＝(－2)kCx10－k 令10－k＝4，解得k＝4，‎ ‎∴展开式中含x4项的系数为(－2)4C＝3360.………(6分)‎ ‎(2)∵第3r项的二项式系数为C，‎ 第r＋2项的二项式系数为C ‎∴C＝C，故3r－1＝r＋1(r∈N)或3r－1＋r＋1＝10(r∈N)，解得r＝1.………(12分)‎ ‎19.（l）先取两本书作为一份，其余每本书为一份，将这六份书分给6个人，有 种分法．………(6分)‎ ‎（2）有两类办法：一人得3本，其余4人各得一本，方法数为 ；‎ 两人各得2本，其余3人各得一本，方法数为 ，‎ 所以所求方法种数为+=16800种..………(12分)‎ ‎20.(1)由题中的直方图知，成绩在[14,16)内的人数为50×(0.16×1)＋50×(0.38×1)＝27(人)，所以该班成绩良好的人数为27人．………(5分)‎ ‎(2)设事件M：“|m－n|＞1”‎ 由频率分布直方图知，成绩在[13,14)的人数为50×0.06×1＝3人，成绩在[17,18)的人数为50×0.08×1＝4人，‎ ‎∴P(M)＝＝.………(12分)‎ ‎21.(1) 当A＝1时，方程为x2＋Bx＋C＝0‎ 方程有实数解 B2－4C≥0‎ B＝1时，不可能 B＝2时，C＝1 1种 B＝3时，C＝1，2 2种 B＝4时，C＝1，2，3，4 4种 B＝5时，C＝1，2，3，4，5，6 6种 B＝6时，C＝1，2，3，4，5，6 6种 共有19种 ………3分 而B、C所有可能取值为6×6＝36种 ‎ ‎∴ 方程有实数根的概率为 ………6分 ‎(2)方程为Ax2－Ax＋A－3＝0‎ 方程有实数解，则 得0＜A≤4‎ 方程的实数解全为正数时 得3＜A≤4 ‎ ‎∴ 方程的实数解全为正数时概率为 故方程至少有一个非正实数根的概率为………(12分)‎ ‎22.(1)将x1＝3，x2＝4分别代入方程－x＋12＝0，得解得 ‎∴f(x)＝(x≠2)．………(5分)‎ ‎(2)不等式即为<，可化为<0，即(x－2)(x－1)(x－k)>0.‎ ‎①当10，解集为(1,2)∪(2，＋∞)；‎ ‎③当k>2时，解集为(1,2)∪(k，＋∞)………(12分)‎