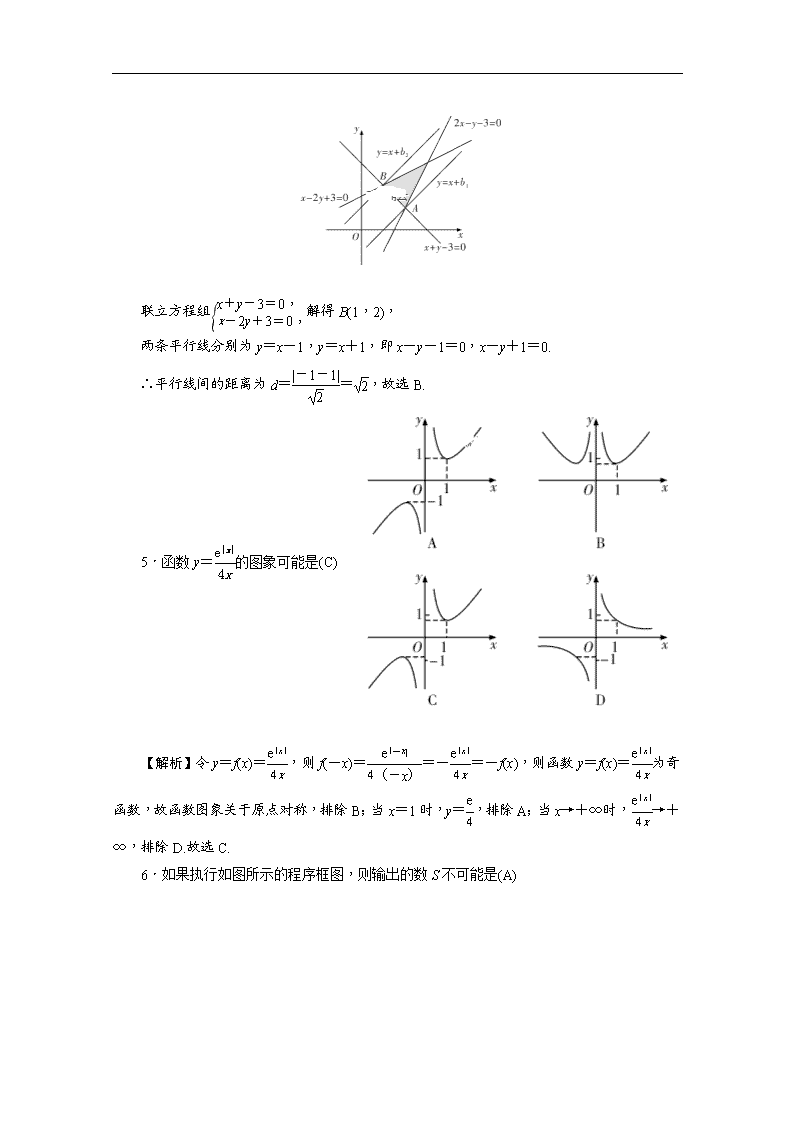湖南师范大学附属中学2020届高三上学期第二次月考数学(理)试题 含解析
数 学(理科)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题的四个选项中,只有一项是符合题目要求的.
1.已知集合A={x|x2-2x-3<0},集合B={x|2x+1>1},则∁BA=(A)
A.[3,+∞) B.(3,+∞)
C.(-∞,-1]∪[3,+∞) D.(-∞,-1)∪(3,+∞)
【解析】A={x|x2-2x-3<0}={x|-1
1}={x|x>-1},∁BA=[3,+∞),故选A.
2.已知函数f(x)=x2+bx+c,则“c<0”是“∃x0∈R,使f(x0)<0”的(A)
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
【解析】已知函数f(x)=x2+bx+c,则“c<0”时,函数与x轴有两个交点,所以“∃x0∈R,使f(x0)<0”成立.而“∃x0∈R,使f(x0)<0”,即x2+bx+c<0,Δ=b2-4c>0,即b2>4c,c不一定有c<0.综上,函数f(x)=x2+bx+c,则“c<0”是“∃x0∈R,使f(x0)<0”的充分不必要条件;故选A.
3.设a=log48,b=log0.48,c=20.4,则(A)
A.bc>b.故选A.
4.若平面区域夹在两条斜率为1的平行直线之间,则这两条平行直线间的距离的最小值为(B)
A. B. C. D.
【解析】作出平面区域如图所示.∴当直线y=x+b分别经过A,B时,平行线间的距离最小,
联立方程组解得A(2,1),
联立方程组解得B(1,2),
两条平行线分别为y=x-1,y=x+1,即x-y-1=0,x-y+1=0.
∴平行线间的距离为d==,故选B.
5.函数y=的图象可能是(C)
【解析】令y=f(x)=,则f(-x)==-=-f(x),则函数y=f(x)=为奇函数,故函数图象关于原点对称,排除B;当x=1时,y=,排除A;当x→+∞时,→+∞,排除D.故选C.
6.如果执行如图所示的程序框图,则输出的数S不可能是(A)
A.0.7 B.0.75
C.0.8 D.0.9
【解析】此程序框图执行的是输入一个正整数n,求++…+的值S,并输出S.S=++…+=1-+-+…+-=.令S等于0.7,解得n=不是正整数,而n分别输入3,4,9时,可分别输出0.75,0.8,0.9.故选A.
7.古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…这样的数成为正方形数.下列数中既是三角形数又是正方形数的是(C)
A.289 B.1024 C.1225 D.1378
【解析】由图形可得三角形数构成的数列通项an=(n+1),
同理可得正方形数构成的数列通项bn=n2,则由bn=n2(n∈N+)可排除D,将A、B、C选项代入an=(n+1)验证知只有1225符合,故选C.
8.已知A、B是圆O:x2+y2=16上的两个动点,||=4,=-.若M是线段AB的中点,则·的值为(C)
A.8+4 B.8-4
C.12 D.4
【解析】因为M是线段AB的中点,所以=+,从而·=·(+)=2-2+·,由圆的方程可知圆O的半径为4,即||=||=4,又因为||=4,所以〈,〉=60°,故·=8,所以·=12.
9.点A、B为椭圆E:+=1(a>b>0)长轴的端点,C、D为椭圆E短轴的端点,动点M满足=2,若△MAB面积的最大值为8,△MCD面积的最小值为1,则椭圆的离心率为(D)
A. B. C. D.
【解析】设A(-a,0),B(a,0),M(x,y).
∵动点M满足=2,则=2,化简得+y2=.
∵△MAB面积的最大值为8,△MCD面积的最小值为1,
∴×2a×a=8,×2b×a=1,解得a=,b=,
∴椭圆的离心率为=.故选D.
10.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是A1B上一动点,则AP+D1P的最小值为(D)
A.2
B.
C.2+
D.
【解析】把对角面A1C绕A1B旋转,使其与△AA1B在同一平面上,连接AD1,则在△AA1D中,AD1==为所求的最小值.故选D.
11.已知函数f(x)=x2-2ln |x|与g(x)=sin(ωx+φ)(ω>0)有两个公共点,则在下列函数中满足条件的周期最大的g(x)=(C)
A.sin B.sin
C.sin D.sin
【解析】因为f(x)=x2-2ln |x|为偶函数,所以当x>0时,f(x)=x2-2ln x,则f′(x)=2x-=,所以f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,所以当x=1时,f(x)min=f(1)=1,所以当x<0时,f(x)min=f(-1)=1,所以g(x)的最大周期是2.所以T==2,ω=π,又g(x)恰好在x=1和x=-1处取得最大值1,故φ=-,故选C.
12.设D是含数1的有限实数集,f(x)是定义在D上的函数.若f(x)的图象绕原点逆时针旋转后与原图象重合,则在以下各项中,f(1)的可能取值只能是(B)
A. B. C. D.0
【解析】记点(1,f(1))为点A1,若f(x)逆时针旋转后与原图象重合,则A1绕原点逆时针旋转后的对应点A2在f(x)图象上,同时有A2绕原点逆时针旋转后的对应点A3也在f(x)图象上,以此类推,则f(x)的图象上至少有以原点为圆心的一个圆周上的12等分的12个点.
当f(x)取值为时,因为OA1与x轴正半轴夹角为,其逆时针旋转时形成的12个散点中,
由圆的对称性知,点A1和A9的横坐标相同,即在同一个x处同时存在2个f(x)值,不符合函数定义,故A项错误.
同理,当f(x)=和0时亦不符合函数定义,故C,D项错误.
故f(x)的可能取值只能是.故正确答案为B.
二、填空题,本大题共4小题,每小题5分,共20分.
13.定积分dx=____.
【解析】dx表示半径为1的四分之一圆的面积.
14.在公差大于0的等差数列{an}中,2a7-a13=1,且a1,a3-1,a6+5成等比数列,则数列{(-1)n-1an}的前21项和为__21__.
【解析】公差d大于0的等差数列{an}中,2a7-a13=1,可得2a1+12d-(a1+12d)=1,即a1=1,由a1,a3-1,a6+5成等比数列,可得(a3-1)2=a1(a6+5),即为(1+2d-1)2=1+5d+5,解得d=2(负值舍去),
则an=1+2(n-1)=2n-1,n∈N*,
所以数列{(-1)n-1an}的前21项和为a1-a2+a3-a4+…+a19-a20+a21=1-3+5-7+…+37-39+41=-2×10+41=21.
15.若函数y=f(x)的图象上存在两个点A,B关于原点对称,则称点对[A,B]为y=f(x)的“友情点对”,点对[A,B]与[B,A]可看作同一个“友情点对”,若函数f(x)=恰好有两个“友情点对”,则实数a的值为__2__.
【解析】由题意可知-x3+6x2-9x+a=-2在(0,+∞)上有两解,即a=x3-6x2+9x-2在(0,+∞)上有两解,
设g(x)=x3-6x2+9x-2,
则g′(x)=3x2-12x+9,令g′(x)=0得x=1或x=3.
∴当00,当13时,g′(x)>0,
∴g(x)在(0,1)上单调递增,在[1,3)上单调递减,在[3,+∞)上单调递增,
∴当x=1时,g(x)取得极大值g(1)=2,当x=3时,g(x)取得极小值g(3)=-2.
作出g(x)的函数图象如图所示:
∵a=x3-6x2+9x-2在(0,+∞)上有两解,∴a=2.
16.点M为棱长是2的正方体ABCD-A1B1C1D1的内切球O球面上的动点,点N为B1C1的中点,若满足DM⊥BN,则动点M的轨迹的长度为____.
【解析】如图,正方体ABCD-A1B1C1D1的内切球O的半径R=,
由题意,取BB1的中点H,连接CH,
则CH⊥NB,DC⊥NB,∴NB⊥平面DCH,
∴动点M的轨迹就是平面DCH与内切球O的交线,
∵正方体ABCD-A1B1C1D1的棱长是2,
∴O到平面DCH的距离为d=,截面圆的半径r==,
所以动点M的轨迹的长度为截面圆的周长2πr=.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(本小题满分12分)
在△ABC中,内角A,B,C的对边分别为a,b,c.已知=.
(1)求的值;
(2)若cos B=,b=2,求△ABC的面积S.
【解析】(1)由正弦定理,得=,2分
所以=.即(cos A-2cos C)sin B=(2sin C-sin A)cos B,
化简可得sin(A+B)=2sin(B+C).4分
又A+B+C=π,所以sin C=2sin A,
因此=2.6分
(2)由=2得c=2a.由余弦定理b2=a2+c2-2accos B 及cos B=, b=2,
得4=a2+4a2-4a2×,解得a=1,从而c=2.9分
又因为cos B=,且00,t∈R),又B(1,2,0),C(-1,2,0),
所以=(0,t,s),=(-1,t-2,s),6分
由(1)知OF⊥BC,故OF与平面BCF垂直,等价于OF⊥BF,
故·=0,从而t(t-2)+s2=0,即t2-2t+s2=0,
直线l上存在唯一一点F使得直线OF与平面BCF垂直,即关于t的方程有唯一实数解,
所以Δ=4-4s2=0,解得s=1,此时t=1.8分
故点E的坐标为(0,0,1),点F的坐标为(0,1,1).
因为OF⊥平面FBC,所以OF⊥BF且OF⊥CF,所以∠BFC即二面角B—OF—C的平面角.10分
因为=(1,1,-1),=(-1,1,-1),
所以cos∠BFC==,
即若直线l上存在唯一一点F使得直线OF与平面BCF垂直时,
二面角B—OF—C的余弦值为.12分
20.(本小题满分12分)
已知抛物线C的顶点为O(0,0),焦点F为(0,1).
(1)求抛物线C的方程;
(2)过点F作直线交抛物线C于A,B两点,若直线AO、BO分别交直线l:y=x-2于M,N两点,求|MN|的最小值.
【解析】(1)由已知可设抛物线的方程为:x2=2py(p>0),则=1⇒p=2,
所以抛物线C的方程是x2=4y.2分
(2)设A,B,所以kAO=,kBO=,所以直线AO的方程是:y=x,
由∴xM=,同理由∴xN=.
所以|MN|=|xM-xN|==8,①5分
设AB:y=kx+1,由∴x2-4kx-4=0,∴
且|x1-x2|==4,代入①得到:
|MN|=8·=8·,7分
设4k-3=t,t≠0,则k=,
①当t>0时,
|MN|=8=2>2;9分
②当t<0时,
|MN|=8=2=2≥2×=,
当t=-时,|MN|取得最小值,此时,k=-;11分
综上所述:|MN|的最小值是.12分
21.(本小题满分12分)
已知函数f(x)=x2ln x.
(1)求函数f(x)的单调区间;
(2)证明: 对任意的t>0, 存在唯一的s, 使t=f(s).
(3)设(2)中所确定的s关于t的函数为s=g(t), 证明: 当t>e2时,有<<.
【解析】(1)函数f(x)的定义域为(0,+∞).
f′(x)=2xln x+x=x(2ln x+1),令f′(x)=0,得x=.
当x变化时,f′(x),f(x)的变化情况如下表:
x
f′(x)
-
0
+
f(x)
极小值
所以函数f(x)的单调递减区间是,单调递增区间是.2分
(2)证明:当00,令h(x)=f(x)-t,x∈[1,+∞),由(1)知,h(x)在区间(1,+∞)内单调递增,h(1)=-t<0,
h(et)=e2tln et-t=t(e2t-1)>0.故存在唯一的s∈(1,+∞),使得t=f(s)成立.6分
(3)证明:因为s=g(t),由(2)知,t=f(s),且s>1,
从而====,其中u=ln s.7分
要使<<成立,只需0e2时,若s=g(t)≤e,则由f(s)的单调性,有t=f(s)≤f(e)=e2,矛盾.
所以s>e,即u>1,从而ln u>0成立.9分
另一方面,令F(u)=ln u-,u>1.F′(u)=-,令F′(u)=0,得u=2.
当10;当u>2时,F′(u)<0.
故对u>1,F(u)≤F(2)<0,因此ln u<成立.11分
综上,当t>e2时,有<<.12分
(二)选考题:共10分.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本小题满分10分)选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,曲线C的参数方程为(α为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin=.
(1)求C的普通方程和l的倾斜角;
(2)设点P(0,2),l和C交于A,B两点,求|PA|+|PB|.
【解析】由消去参数α,得+y2=1,
即C的普通方程为+y2=1.2分
由ρsin=,得ρsin θ-ρcos θ=2, ①
将代入①得y=x+2.4分
所以直线l的斜率角为.5分
(2)由(1)知,点P(0,2)在直线l上,可设直线l的参数方程为(t为参数),
即(t为参数),
代入+y2=1并化简得5t2+18+27=0,7分
Δ=(18)2-4×5×27=108>08分
设A,B两点对应的参数分别为t1,t2.
则t1+t2=-<0,t1t2=>0,所以t1<0,t2<0.
所以|PA|+|PB|=|t1|+|t2|=.10分
23.(本小题满分10分)选修4—5:不等式选讲
已知函数f(x)=|x-1|+|x-3|.
(1)解不等式f(x)≤x+1;
(2)设函数f(x)的最小值为c,实数a,b满足a>0,b>0,a+b=c,求证:+≥1.
【解析】(1)f(x)≤x+1,即|x-1|+|x-3|≤x+1.
①当x<1时,不等式可化为4-2x≤x+1,解得x≥1,
又∵x<1,∴x∈∅;
②当1≤x≤3时,不等式可化为2≤x+1,解得x≥1,
又∵1≤x≤3,∴1≤x≤3.
③当x>3时,不等式可化为2x-4≤x+1,解得x≤5,
又∵x>3,∴31,n>1,a=m-1,b=n-1,m+n=4,
+=+=m+n++-4=≥=1,
原不等式得证.10分