江西省抚州市临川第二中学2020届高三上学期第一次月考数学（理）试题 含解析

江西省抚州市临川第二中学2020届高三上学期第一次月考数学（理）试题 含解析

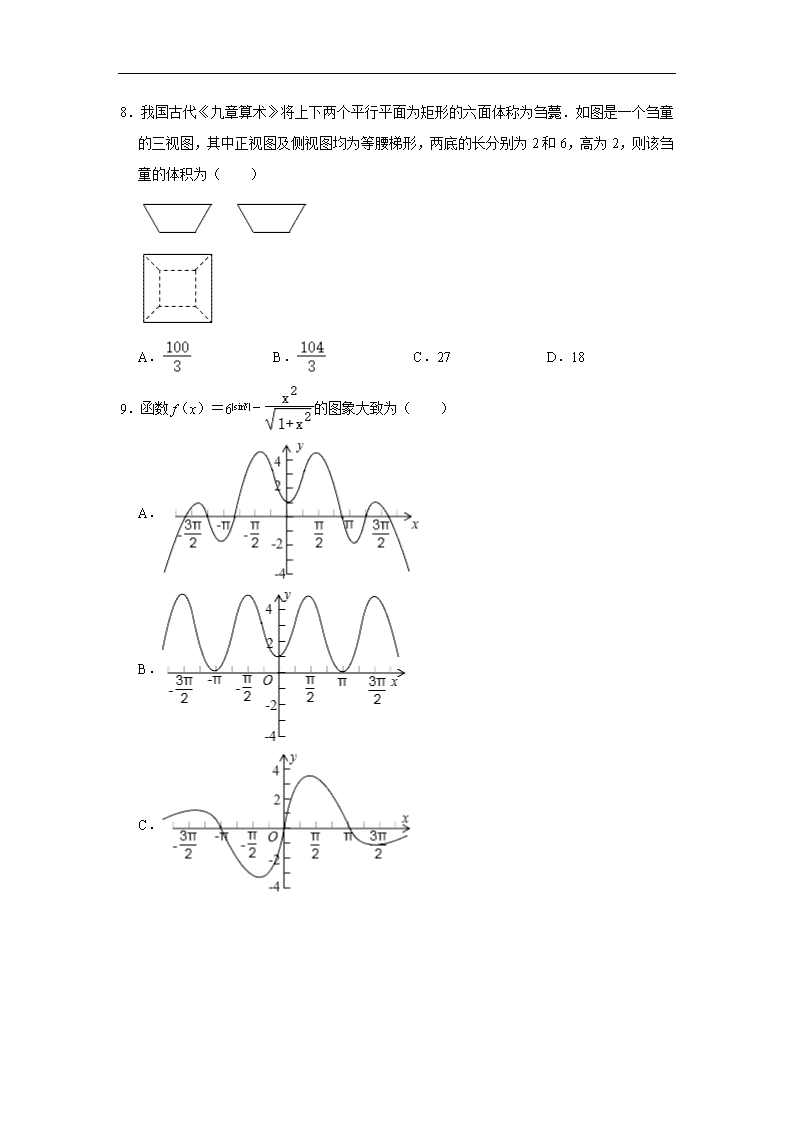
‎2019-2020学年江西省抚州市临川二中高三（上）第一次考试数学试卷（理科）‎ 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1．已知集合，则A∩B＝（　　）‎ A．{x|﹣3≤x≤1} B．{x|0≤x≤1} C．{x|﹣3≤x＜1} D．{x|﹣1≤x≤0}‎ ‎2．设复数z＝，则|z|＝（　　）‎ A． B． C． D．‎ ‎3．在等差数列{an}中，若a3＝5，S4＝24，则a9＝（　　）‎ A．﹣5 B．﹣7 C．﹣9 D．﹣11‎ ‎4．已知幂函数f（x）＝xα的图象经过点 （3，5），且a＝（）α，b＝，c＝logα，则a，b，c的大小关系为（　　）‎ A．c＜a＜b B．a＜c＜b C．a＜b＜c D．c＜b＜a ‎5．为了贯彻落实党中央精准扶贫决策，某市将其低收入家庭的基本情况经过统计绘制如图，其中各项统计不重复．若该市老年低收入家庭共有900户，则下列说法错误的是（　　）‎ A．该市总有 15000 户低收入家庭 ‎ B．在该市从业人员中，低收入家庭共有 1800 户 ‎ C．在该市无业人员中，低收入家庭有 4350 户 ‎ D．在该市大于 18 岁在读学生中，低收入家庭有 800 户 ‎6．平面内不共线的三点O，A，B，满足||＝1，||＝2，点C为线段AB的中点，若||＝，则∠AOB＝（　　）‎ A． B． C． D．‎ ‎7．（1+2x﹣）8的展开式中x2y2项的系数是（　　）‎ A．420 B．﹣420 C．1680 D．﹣1680‎ ‎8．我国古代《九章算术》将上下两个平行平面为矩形的六面体称为刍薨．如图是一个刍童的三视图，其中正视图及侧视图均为等腰梯形，两底的长分别为2和6，高为2，则该刍童的体积为（　　）‎ A． B． C．27 D．18‎ ‎9．函数f（x）＝6|sinx|﹣的图象大致为（　　）‎ A． ‎ B． ‎ C． ‎ D．‎ ‎10．太极图被称为“中华第一图”．从孔庙大成殿粱柱，到楼观台、三茅宫标记物；从道袍、卦摊、中医、气功、武术到南韩国旗……，太极图无不跃居其上．这种广为人知的太极图，其形状如阴阳两鱼互抱在一起，因而被称为“阴阳鱼太极图”．在如图所示的阴阳鱼图案中，阴影部分可表示为A＝{（x，y）}，设点（x，y）∈A，则z＝x+2y的取值范围是（　　）‎ A．[﹣2﹣，2] B．[﹣2，2] C．[﹣2，2+] D．[﹣4，2+]‎ ‎11．关于函数f（x）＝|cosx|+cos|2x|有下列四个结论：①f（x）是偶函数；②π是f（x）的最小正周期；③f（x）在[π，π]上单调递增；④f（x）的值域为[﹣2，2]．上述结论中，正确的个数为（　　）‎ A．1 B．2 C．3 D．4‎ ‎12．已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推，若该数列前n项和N满足：①N＞80②N是2的整数次幂，则满足条件的最小的n为（　　）‎ A．21 B．91 C．95 D．101‎ 二、填空题（本大题共4小题，每小题5分，共20分．）‎ ‎13．椭圆＝1的离心率是　 　．‎ ‎14．设某总体是由编号为01，02，……，19，20的20个个体组成，利用下面的随机数表选取6个个体，选取方法是从随机数表第1行的第3列数字开始从左到右依次选取两个数字，则选出来的第6个个体编号为　 　．‎ ‎1818 0792 4544 1716 5809 7983 8617第1行 ‎6206 7650 0310 5523 6405 0526 6238第2行 ‎15．已知点A（0，1），抛物线C：y2＝ax（a＞0）的焦点为F，连接FA，与抛物线C相交于点M，延长FA，与抛物线C的准线相交于点N，若|FM|：|MN|＝1：2，则实数a的值为　 　．‎ ‎16．已知四棱锥S﹣ABCD的底面为矩形，SA⊥底面ABCD，点E在线段BC上，以AD为直径的圆过点 E．若SA＝AB＝3，则△SED面积的最小值为　 　．‎ 三、解答题（本大题共5小题，共70分，解答应写出文字说明，证明过程或演算步骤．第17～21题为必考题，每道试题考试必须作答，第22、23题为选考题，考生根据要求作答．）（一）必考题：共60分 ‎17．在△ABC中，内角A，B，C的对边分别是a，b，c，且（a﹣b）2＝c2﹣ab．‎ ‎（1）求角C；‎ ‎（2）若4ccos（A+）+bsinC＝0，且a＝1，求△ABC的面积．‎ ‎18．如图，在三棱锥P﹣ABC中，AC＝BC，AB＝2BC，D为线段AB上一点，且AD＝3DB，PD⊥平面ABC，PA与平面ABC所成的角为45°．‎ ‎（1）求证：平面PAB⊥平面PCD；‎ ‎（2）求二面角P﹣AC﹣D的平面角的余弦值．‎ ‎19．已知椭圆C：+y2＝1，不与坐标轴垂直的直线l与椭圆C相交于M，N两点．‎ ‎（1）若线段MN的中点坐标为 （1，），求直线l的方程；‎ ‎（2）若直线l过点P（p，0），点Q（q，0）满足kQM+kQN＝0，求pq的值．‎ ‎20．某机构组织的家庭教育活动上有一个游戏，每次由一个小孩与其一位家长参与，测试家长对小孩饮食习惯的了解程度．在每一轮游戏中，主持人给出A，B，C，D四种食物，要求小孩根据自己的喜爱程度对其排序，然后由家长猜测小孩的排序结果．设小孩对四种食物排除的序号依次为xAxBxCxD，家长猜测的序号依次为yAyByCyD，其中xAxBxCxD和yAyByCyD都是1，2，3，4四个数字的一种排列．定义随机变量X＝（xA﹣yA）2+（xB﹣yB）2+（xC﹣yC）2+（xD﹣yD）2，用X来衡量家长对小孩饮食习惯的了解程度．‎ ‎（1）若参与游戏的家长对小孩的饮食习惯完全不了解．‎ ‎（ⅰ）求他们在一轮游戏中，对四种食物排出的序号完全不同的概率；‎ ‎（ⅱ）求X的分布列（简要说明方法，不用写出详细计算过程）；‎ ‎（2）若有一组小孩和家长进行来三轮游戏，三轮的结果都满足X＜4，请判断这位家长对小孩饮食习惯是否了解，说明理由．‎ ‎21．已知函数f（x）＝ln（ax+b）﹣x（a，b∈R，ab≠0）．‎ ‎（1）讨论f（x）的单调性；‎ ‎（2）若f（x）≤0恒成立，求ea（b﹣1）的最大值．‎ 四、（二）选考题：请考生在第（22）、（23）两题中任选一题作答．注意：只能做所选定的题目，如果多做，则按所做的第一个题目计分．选修4-4：坐标系与参数方程 ‎22．在平面直角坐标系xOy中，曲线C的参数方程为（m为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos（θ+）＝1．‎ ‎（1）求直线l的直角坐标方程和曲线C的普通方程；‎ ‎（2）已知点M （2，0），若直线l与曲线C相交于P、Q两点，求的值．‎ ‎[选修4-5：不等式选讲]‎ ‎23．已知x，y，z均为正数．‎ ‎（1）若xy＜1，证明：|x+z|⋅|y+z|＞4xyz；‎ ‎（2）若＝，求2xy⋅2yz⋅2xz的最小值．‎ ‎2019-2020学年江西省抚州市临川二中高三（上）第一次考试数学试卷（理科）‎ 参考答案与试题解析 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1．已知集合，则A∩B＝（　　）‎ A．{x|﹣3≤x≤1} B．{x|0≤x≤1} C．{x|﹣3≤x＜1} D．{x|﹣1≤x≤0}‎ ‎【解答】解：解一元二次不等式x2+2x﹣3≤0得：﹣3≤x≤1，即A＝{x|﹣3≤x≤1}，‎ 解根式不等式＜2得：0≤x＜4，即B＝{x|0≤x＜4}，‎ 即A∩B＝，‎ 故选：B．‎ ‎2．设复数z＝，则|z|＝（　　）‎ A． B． C． D．‎ ‎【解答】解：z＝＝＝＝﹣﹣i，‎ 则|z|＝＝＝＝，‎ 故选：D．‎ ‎3．在等差数列{an}中，若a3＝5，S4＝24，则a9＝（　　）‎ A．﹣5 B．﹣7 C．﹣9 D．﹣11‎ ‎【解答】解：数列{an}为等差数列，设首项为a1，公差为d，‎ ‎∵a3＝5，S4＝24，‎ ‎∴a1+2d＝5，4a1+d＝24，‎ 联立解得a1＝9，d＝﹣2，‎ 则a9＝9﹣2×8＝﹣7．‎ 故选：B．‎ ‎4．已知幂函数f（x）＝xα的图象经过点 （3，5），且a＝（）α，b＝，c＝logα，则a，b，c的大小关系为（　　）‎ A．c＜a＜b B．a＜c＜b C．a＜b＜c D．c＜b＜a ‎【解答】解：∵幂函数f（x）＝xα的图象经过点 （3，5），‎ ‎∴3α＝5，∴α＝log35∈（1，2），‎ ‎∴0＜a＝（）α＜1，‎ b＝＞1，‎ c＝logα＜logα1＝0，‎ ‎∴c＜a＜b．‎ 故选：A．‎ ‎5．为了贯彻落实党中央精准扶贫决策，某市将其低收入家庭的基本情况经过统计绘制如图，其中各项统计不重复．若该市老年低收入家庭共有900户，则下列说法错误的是（　　）‎ A．该市总有 15000 户低收入家庭 ‎ B．在该市从业人员中，低收入家庭共有 1800 户 ‎ C．在该市无业人员中，低收入家庭有 4350 户 ‎ D．在该市大于 18 岁在读学生中，低收入家庭有 800 户 ‎【解答】解：由题意知，该市老年低收入家庭共有900户，所占比例为6%，‎ 则该市总有低收入家庭900÷6%＝15000（户），A正确；‎ 该市从业人员中，低收入家庭共有15000×12%＝1800（户），B正确；‎ 该市无业人员中，低收入家庭有15000×29%%＝4350（户），C正确；‎ 该市大于18 岁在读学生中，低收入家庭有15000×4%＝600（户），D错误．‎ 故选：D．‎ ‎6．平面内不共线的三点O，A，B，满足||＝1，||＝2，点C为线段AB的中点，若||＝，则∠AOB＝（　　）‎ A． B． C． D．‎ ‎【解答】解：延长OC到E，使得CE＝OC＝，连AE，BE，‎ 则四边形OAEB为平行四边形，‎ ‎∴BE＝1，∴cos∠OBE＝＝，∴∠OBE＝，‎ ‎∴∠AOB＝π﹣∠OBE＝π﹣＝．‎ 故选：C．‎ ‎7．（1+2x﹣）8的展开式中x2y2项的系数是（　　）‎ A．420 B．﹣420 C．1680 D．﹣1680‎ ‎【解答】解：（1+2x﹣）8的展表示8个因式（1+2x﹣）的乘积，故其中有2个因式取2x，有2个因式取﹣，其余的4个因式都取1，可得含x2y2的项．‎ 故展开式中x2y2项的系数是•22•••＝420，‎ 故选：A．‎ ‎8．我国古代《九章算术》将上下两个平行平面为矩形的六面体称为刍薨．如图是一个刍童的三视图，其中正视图及侧视图均为等腰梯形，两底的长分别为2和6，高为2，则该刍童的体积为（　　）‎ A． B． C．27 D．18‎ ‎【解答】解：原图为正四棱台，两底的长分别为2和6，高为2，‎ 该刍薨的体积为，‎ 故选：B．‎ ‎9．函数f（x）＝6|sinx|﹣的图象大致为（　　）‎ A． ‎ B． ‎ C． ‎ D．‎ ‎【解答】解：f（﹣x）＝f（x），则f（x）为偶函数，图象关于y轴对称，排除C，‎ f（π）＝1﹣＜0，排除B，‎ f（）＝6﹣≈6﹣＞4，排除D，‎ 故选：A．‎ ‎10．太极图被称为“中华第一图”．从孔庙大成殿粱柱，到楼观台、三茅宫标记物；从道袍、卦摊、中医、气功、武术到南韩国旗……，太极图无不跃居其上．这种广为人知的太极图，其形状如阴阳两鱼互抱在一起，因而被称为“阴阳鱼太极图”．在如图所示的阴阳鱼图案中，阴影部分可表示为A＝{（x，y）}，设点（x，y）∈A，则z＝x+2y的取值范围是（　　）‎ A．[﹣2﹣，2] B．[﹣2，2] C．[﹣2，2+] D．[﹣4，2+]‎ ‎【解答】解：如图，作直线x+2y＝0，当直线上移与圆x2+（y﹣1）2＝1相切时，z＝x+2y取最大值，‎ 此时，圆心（0，1）到直线z＝x+2y的距离等于1，即，‎ 解得z的最大值为：2+，‎ 当下移与圆x2+y2＝4相切时，x+2y取最小值，‎ 同理，即z的最小值为：﹣2，‎ 所以z∈．‎ 故选：C．‎ ‎11．关于函数f（x）＝|cosx|+cos|2x|有下列四个结论：①f（x）是偶函数；②π是f（x）的最小正周期；③f（x）在[π，π]上单调递增；④f（x）的值域为[﹣2，2]．上述结论中，正确的个数为（　　）‎ A．1 B．2 C．3 D．4‎ ‎【解答】解：f（x）＝|cosx|+cos|2x|＝|cosx|+2cos2|x|﹣1，‎ 由cos|x|＝cosx，可得f（x）＝|cosx|+2cos2x﹣1＝2|cosx|2+|cosx|﹣1，‎ 由f（﹣x）＝2|cos（﹣x）|2+|cos（﹣x）|﹣1＝f（x），则f（x）为偶函数，故①正确；‎ 可令t＝|cosx|，可得g（t）＝2t2+t﹣1，‎ 由y＝|cosx|的最小正周期π，可得f（x）的最小正周期为π，故②正确；‎ 由y＝cosx在[﹣，0]递增，在[0，]递减，可得f（x）在[，π]递增，在[π，]递减，故③错误；‎ 由t∈[0，1]，g（t）＝2（t+）2﹣，可得g（t）在[0，1]递增，则g（t）的值域为[﹣1，2]，故④错误．‎ 故选：B．‎ ‎12．已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推，若该数列前n项和N满足：①N＞80②N是2的整数次幂，则满足条件的最小的n为（　　）‎ A．21 B．91 C．95 D．101‎ ‎【解答】解：依题意，因为N满足条件①N＞80②N是2的整数次幂，‎ 所以Sn＝N＝2k，（k∈N*，且k≥7）‎ 如图：第m行各项的和为2m﹣1，‎ 前m行之和＝（21﹣1）+（22﹣1）+……+（2m﹣1）＝（2+22+23+……+2m）﹣m＝2m+1﹣m﹣2，‎ 设满足条件的n在第m+1行，则前m行之和为2m+1﹣m﹣2≤2m+1，故N＝2m+1，‎ 则m+2＝1+2+4+……+2s，‎ 则满足条件的m的最小值为13，且N为第14行的第4项．‎ 所以n＝+4＝95．‎ 故选：C．‎ 二、填空题（本大题共4小题，每小题5分，共20分．）‎ ‎13．椭圆＝1的离心率是　　．‎ ‎【解答】解：由椭圆的标准方程可知，a＝2，b＝，‎ ‎∴c＝＝1‎ ‎∴e＝＝．‎ 故答案为：．‎ ‎14．设某总体是由编号为01，02，……，19，20的20个个体组成，利用下面的随机数表选取6个个体，选取方法是从随机数表第1行的第3列数字开始从左到右依次选取两个数字，则选出来的第6个个体编号为　06　．‎ ‎1818 0792 4544 1716 5809 7983 8617第1行 ‎6206 7650 0310 5523 6405 0526 6238第2行 ‎【解答】解：由题意依次选取的样本编号为：18，07，17，16，09，（17重复，舍去）06；‎ 所以选出来的第6个个体编号为06．‎ 故答案为：06．‎ ‎15．已知点A（0，1），抛物线C：y2＝ax（a＞0）的焦点为F，连接FA，与抛物线C 相交于点M，延长FA，与抛物线C的准线相交于点N，若|FM|：|MN|＝1：2，则实数a的值为　　．‎ ‎【解答】解：抛物线C：y2＝ax（a＞0）的焦点为F（，0），准线方程为x＝﹣，‎ 可得直线AF的方程为y＝1﹣x，‎ 设M（x1，y1），N（﹣，y2），可得y2＝1﹣•（﹣）＝2，‎ 由|FM|：|MN|＝1：2，可得＝，‎ 可得y1＝，代入直线方程可得x1＝，‎ 代入抛物线方程可得＝a•，‎ 可得a＝．‎ 故答案为：．‎ ‎16．已知四棱锥S﹣ABCD的底面为矩形，SA⊥底面ABCD，点E在线段BC上，以AD为直径的圆过点 E．若SA＝AB＝3，则△SED面积的最小值为　　．‎ ‎【解答】解：设BE＝x，EC＝y，则BC＝AD＝x+y，‎ ‎∵SA⊥平面ABCD，ED⊂平面ABCD，∴SA⊥ED，‎ ‎∵AE⊥ED，SA∩AE＝A，∴ED⊥平面SAE，∴ED⊥SE，‎ 由题意得AE＝，ED＝，‎ 在Rt△AED中，AE2+ED2＝AD2，∴x2+3+y2+3＝（x+y）2，‎ 化简，得xy＝3，‎ 在Rt△SED中，SE＝，ED＝＝，‎ ‎∴S△SED＝＝，‎ ‎∵3x2+≥2＝36，‎ 当且仅当x＝，‎ 时，等号成立，∴＝．‎ ‎∴△SED面积的最小值为．‎ 故答案为：．‎ 三、解答题（本大题共5小题，共70分，解答应写出文字说明，证明过程或演算步骤．第17～21题为必考题，每道试题考试必须作答，第22、23题为选考题，考生根据要求作答．）（一）必考题：共60分 ‎17．在△ABC中，内角A，B，C的对边分别是a，b，c，且（a﹣b）2＝c2﹣ab．‎ ‎（1）求角C；‎ ‎（2）若4ccos（A+）+bsinC＝0，且a＝1，求△ABC的面积．‎ ‎【解答】（1）由（a﹣b）2＝c2﹣ab，得a2+b2﹣c2＝ab，‎ 所以由余弦定理，得，‎ 又因为C∈（0，π），‎ 所以；‎ ‎（2）由，得，得﹣4csinA+bsinC＝0，‎ 由正弦定理，得4ca＝bc．‎ 因为c≠0，所以4a＝b，‎ 又因a＝1，所以b＝4，‎ 所以△ABC的面积．‎ ‎18．如图，在三棱锥P﹣ABC中，AC＝BC，AB＝2BC，D为线段AB上一点，且AD＝3DB，PD⊥平面ABC，PA与平面ABC所成的角为45°．‎ ‎（1）求证：平面PAB⊥平面PCD；‎ ‎（2）求二面角P﹣AC﹣D的平面角的余弦值．‎ ‎【解答】解：（1）证明：∵AC＝BC，AB＝2BC，‎ ‎∴，∴AB2＝AC2+BC2，∴AC⊥BC，‎ 在Rt△ABC中，由AC＝BC，得∠CAB＝30°，‎ 设BD＝1，由AD＝3BD，得AD＝3，BC＝2，AC＝2，‎ 在△ACD中，由余弦定理得CD2＝AD2+AC2﹣2AD•ACcos30°＝3，‎ ‎∴CD＝，‎ ‎∴CD2+AD2＝AC2，∴CD⊥AD，‎ ‎∵PD⊥平面ABC，CD⊂平面ABC，∴PD⊥CD，‎ 又PD∩AD＝D，∴CD⊥平面PAB，‎ 又CD⊂平面PCD，∴平面PAB⊥平面PCD．‎ ‎（2）解：∵PD⊥平面ABC，∴PA与平面ABC所成角为∠PAD，即∠PAD＝45°，‎ ‎∴△PAD为等腰直角三角形，PD＝AD，‎ 由（1）得PD＝AD＝3，以D为坐标原点，‎ 分别以DC，DB，DP所在直线为x，y，z轴，建立空间直角坐标系，‎ 则D（0，0，0），C（，0，0），A（0，﹣3，0），P（0，0，3），‎ ‎＝（0，﹣3，﹣3），＝（），‎ 则＝＝（0，0，3）是平面ACD的一个法向量，‎ 设平面PAC的一个法向量＝（x，y，z），‎ 则，取x＝，得＝（，﹣1，1），‎ 设二面角P﹣AC﹣D的平面角为θ，‎ 则cosθ＝＝，‎ ‎∴二面角P﹣AC﹣D的平面角的余弦值为．‎ ‎19．已知椭圆C：+y2＝1，不与坐标轴垂直的直线l与椭圆C相交于M，N两点．‎ ‎（1）若线段MN的中点坐标为 （1，），求直线l的方程；‎ ‎（2）若直线l过点P（p，0），点Q（q，0）满足kQM+kQN＝0，求pq的值．‎ ‎【解答】解：（1）设M（x1，y1），N（x2，y2），则，两式相减，可得 ‎，①‎ 由题意可知x1+x2＝2，y1+y2＝1，代入①可得直线MN的斜率k＝＝﹣，‎ 所以直线MN的方程y﹣＝﹣（x﹣1），即x+2y﹣2＝0，‎ 所以直线MN的方程x+2y﹣2＝0；‎ ‎（2）由题意可知设直线MN的方程y＝k（x﹣p），M（x1，y1），N（x2，y2），‎ 联立，整理得（1+4k2）x2﹣8k2px+4k2p2﹣4＝0，‎ 则x1+x2＝，，x1x2＝，‎ 由kQM+kQN＝0，则+＝0，‎ 即y1（x2﹣q）+y2（x1﹣q）＝0，‎ ‎∴k（x1﹣p）（x2﹣q）+k（x2﹣p）（x1﹣q）＝0，化简得2x1x2﹣（p+q）（x1+x2）+2pq＝0，‎ ‎∴﹣﹣+2pq＝0，‎ 化简得：2pq﹣8＝0，‎ ‎∴pq＝4．‎ ‎20．某机构组织的家庭教育活动上有一个游戏，每次由一个小孩与其一位家长参与，测试家长对小孩饮食习惯的了解程度．在每一轮游戏中，主持人给出A，B，C，D四种食物，要求小孩根据自己的喜爱程度对其排序，然后由家长猜测小孩的排序结果．设小孩对四种食物排除的序号依次为xAxBxCxD，家长猜测的序号依次为yAyByCyD，其中xAxBxCxD和yAyByCyD都是1，2，3，4四个数字的一种排列．定义随机变量X＝（xA﹣yA）2+（xB﹣yB）2+（xC﹣yC）2+（xD﹣yD）2，用X来衡量家长对小孩饮食习惯的了解程度．‎ ‎（1）若参与游戏的家长对小孩的饮食习惯完全不了解．‎ ‎（ⅰ）求他们在一轮游戏中，对四种食物排出的序号完全不同的概率；‎ ‎（ⅱ）求X的分布列（简要说明方法，不用写出详细计算过程）；‎ ‎（2）若有一组小孩和家长进行来三轮游戏，三轮的结果都满足X＜4，请判断这位家长对小孩饮食习惯是否了解，说明理由．‎ ‎【解答】解：（1）（i）若家长对小孩子的饮食习惯完全不了解，‎ 则家长对小孩的排序是随意猜测的，‎ 先考虑小孩的排序为xA，xB，xC，xD为1234的情况，家长的排序有＝24种等可能结果，‎ 其中满足“家长的排序与对应位置的数字完全不同”的情况有9种，分别为：‎ ‎2143，2341，2413，3142，3412，3421，4123，4312，4321，‎ ‎∴家长的排序与对应位置的数字完全不同的概率P＝．‎ 基小孩对四种食物的排序是其他情况，‎ 只需将角标A，B，C，D按照小孩的顺序调整即可，‎ 假设小孩的排序xA，xB，xC，xD为1423的情况，四种食物按1234的排列为ACDB，‎ 再研究yAyByCyD的情况即可，其实这样处理后与第一种情况的计算结果是一致的，‎ ‎∴他们在一轮游戏中，对四种食物排出的序号完全不同的概率为．‎ ‎（ii）根据（i）的分析，同样只考虑小孩排序为1234的情况，家长的排序一共有24种情况，‎ 列出所有情况，分别计算每种情况下的x的值，‎ X的分布列如下表：‎ ‎ X ‎ 0‎ ‎2‎ ‎ 4‎ ‎ 6‎ ‎ 8‎ ‎ 10‎ ‎ 12‎ ‎ 14‎ ‎ 16‎ ‎ 18‎ ‎ 20‎ ‎ P ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎（2）这位家长对小孩的饮食习惯比较了解．‎ 理由如下：‎ 假设家长对小孩的饮食习惯完全不了解，由（1）可知，在一轮游戏中，‎ P（X＜4）＝P（X＝0）+P（X＝2）＝，‎ 三轮游戏结果都满足“X＜4”的概率为（）3＝，‎ 这个结果发生的可能性很小，‎ ‎∴这位家长对小孩饮食习惯比较了解．‎ ‎21．已知函数f（x）＝ln（ax+b）﹣x（a，b∈R，ab≠0）．‎ ‎（1）讨论f（x）的单调性；‎ ‎（2）若f（x）≤0恒成立，求ea（b﹣1）的最大值．‎ ‎【解答】解：（1）①当a＞0时，则f（x）的定义域为（﹣，+∞），‎ ‎＝，由f′（x）＝0，‎ 得x＝1﹣＞﹣，‎ 所以f（x）在（﹣，1﹣）单调递增，在（1﹣，+∞）单调递减，‎ ‎②当a＜0时，则f（x）的定义域为（﹣∞，﹣），‎ 由f′（x）＝0得x＝1﹣＞﹣，‎ 所以f（x）在（﹣∞，﹣）单调递减，（也可由符合函数单调性得出）．‎ ‎（2）由（1）知：当a＜0时，取x0＜且x0＜0时，‎ f（x0）＞ln（a×+b）﹣x0＞0，与题意不合，‎ 当a＞0时，f（x）max＝f（1﹣）＝lna﹣1+≤0，即b﹣1≤a﹣alna﹣1，‎ 所以ea（b﹣1）≤（a﹣alna﹣1）ea，令h（x）＝（x﹣xlnx﹣1）ex，‎ 则h′（x）＝（x﹣xlnx﹣lnx﹣1）ex，‎ 令u（x）＝x﹣xlnx﹣lnx﹣1，则u′（x）＝﹣lnx﹣，‎ 则u″（x）＝，‎ u′（x）在（0，1）上单调递增，在（1，+∞）上单调递减．‎ 则u′（x）max＝u′（1）＜0，‎ 从而u（x）在（0，+∞）单调递减，又因为u（1）＝0．‎ 所以当x∈（0，1）时，u（x）＞0，即h′（x）＞0；‎ 当x∈（1，+∞）时，u（x）＜0，即h′（x）＜0，‎ 则h（x）在（0，1）单调递增，在（1，+∞）单调递减，‎ 所以h（x）max＝h（1）＝0．‎ 四、（二）选考题：请考生在第（22）、（23）两题中任选一题作答．注意：只能做所选定的题目，如果多做，则按所做的第一个题目计分．选修4-4：坐标系与参数方程 ‎22．在平面直角坐标系xOy中，曲线C的参数方程为（m为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos（θ+）＝1．‎ ‎（1）求直线l的直角坐标方程和曲线C的普通方程；‎ ‎（2）已知点M （2，0），若直线l与曲线C相交于P、Q两点，求的值．‎ ‎【解答】解：（1）曲线C的参数方程为（m为参数），两式相加得到m ‎，进一步转换为．直线l的极坐标方程为ρcos（θ+）＝1，转换为直角坐标方程为．‎ ‎（2）将直线的方程转换为参数方程为（t为参数），代入得到（t1和t2为P、Q对应的参数），所以，，‎ 所以＝．‎ ‎[选修4-5：不等式选讲]‎ ‎23．已知x，y，z均为正数．‎ ‎（1）若xy＜1，证明：|x+z|⋅|y+z|＞4xyz；‎ ‎（2）若＝，求2xy⋅2yz⋅2xz的最小值．‎ ‎【解答】解：（1）证明：∵x，y，z均为正数，‎ ‎∴|x+z|⋅|y+z|＝（x+z）（y+z）≥＝，‎ 当且仅当x＝y＝z时取等号．‎ 又∵0＜xy＜1，∴，‎ ‎∴|x+z|⋅|y+z|＞4xyz；‎ ‎（2）∵＝，∴．‎ ‎∵，，，‎ 当且仅当x＝y＝z＝1时取等号，‎ ‎∴，‎ ‎∴xy+yz+xz≥3，∴2xy⋅2yz⋅2xz＝2xy+yz+xz≥8，‎ ‎∴2xy⋅2yz⋅2xz的最小值为8．‎