数学文卷·2019届甘肃省武威市第六中学高二上学期第二次学段考试（2017-11）

数学文卷·2019届甘肃省武威市第六中学高二上学期第二次学段考试（2017-11）

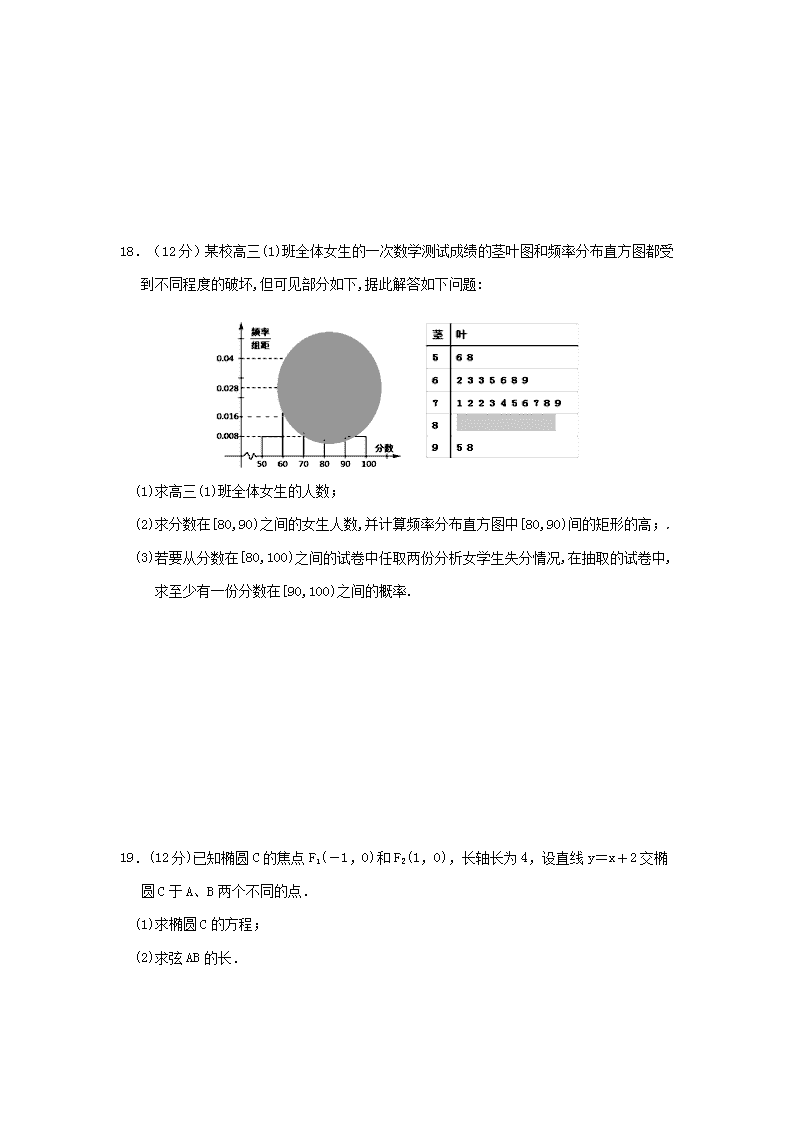
武威六中2017-2018学年度第一学期 高二数学（文）模块学习第二次学段性检测试卷 一、选择题（每小题5分，共60分）‎ ‎1.若原命题:若则, 则其逆命题、否命题、逆否命题中（ ）‎ A.都真 B.都假 C.否命题真 D.逆否命题真 ‎2.在某校的一次英语听力测试中用以下茎叶图记录了 ‎ 甲、乙两组各5名学生的听力成绩(单位：分)已知甲【来源：全,品…中&高*考+网】‎ 组数据的众数为15，乙组数据的中位数为17，则 的值分别为( )‎ A.2，5 B.5，5 C.5，7 D.8，7‎ ‎3．命题“，”的否定是（ ）‎ A．， B．，‎ C．， D．不存在，‎ ‎4.已知正数满足，那么的最小值为（ ）‎ A．10 B．12 C． D.‎ ‎5．以－＝－1的焦点为顶点，顶点为焦点的椭圆方程为 (　 )‎ A.＋＝1 B.＋＝1 C.＋＝1 D.＋＝1‎ ‎6．“”是“”的（ ）‎ A．充分而不必要条件 B．必要而不充分条件 B．充分必要条件 D．既不充分也不必要条件 ‎7．已知命题(R), 命题函数在区间上单调递增, 则下列命题中为真命题的是（ ）‎ A. B. C. D. ‎ ‎8.双曲线－＝1(a>0)的渐近线方程为3x±2y＝0，则a的值为 ( )‎ A．4 B．3 C．2 D．1‎ ‎9.阅读右边的程序框图，运行相应的程序，则输出 的值为 ( )‎ A．3 B．4 C．5 D．6‎ ‎10.已知，则下列各式中正确的不等式是（ ）‎ A. B. ‎ C. D.‎ ‎11.设分别是双曲线的左、右焦点，若双曲线上存在点，使且，则双曲线的离心率为（ ） ‎ A. B． C． D．‎ ‎12 ．若点O和点F分别为椭圆＋＝1的中心和左焦点，点P为椭圆上的任意一点，则 的最大值为（ ）‎ A．6 B．3 C．2 D．8‎ 二、填空题（每空5分，共20分）‎ ‎13.“所有末位数字是0或5的整数能被5整除”的否定形式是 _____‎ ‎14.经过点 A(-1,3)，并且对称轴都在坐标轴上的等轴双曲线的方程为 ‎ ‎15.从长度分别为2，3，4，5的四条线段中任意取出三条,则以这三条线段为边可以构成三角形的概率 ‎ ‎16. 下列结论 ①若命题P：xR,tanx=1；命题q: xR,x-x+1>0,则命题P是真命题;‎ ②“对任意的x,x-a为真命题，a的范围:‎ ③命题“若x-3x+2=0则x=1”的逆否命题：若x1，则x-3x+20 其中正确的是 ______‎ 三、解答题 ‎17．(10分) 求与椭圆有公共焦点，并且离心率为的双曲线方程．‎ ‎18．（12分）某校高三(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:‎ ‎(1)求高三(1)班全体女生的人数；‎ ‎(2)求分数在[80,90)之间的女生人数,并计算频率分布直方图中[80,90)间的矩形的高；‎ ‎(3)若要从分数在[80,100)之间的试卷中任取两份分析女学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100)之间的概率.‎ ‎19．(12分)已知椭圆C的焦点F1(－1，0)和F2(1，0)，长轴长为4，设直线y＝x＋2交椭圆C于A、B两个不同的点．‎ ‎(1)求椭圆C的方程；‎ ‎(2)求弦AB的长．‎ ‎20. (12分)已知，在圆上任取P, 过点P作轴的垂线段PD,D 为垂足，当点P在圆上运动时，求线段PD的中点M的轨迹方程.‎ ‎21．(12分)命题p：关于x的不等式对一切恒成立； 【来源：全,品…中&高*考+网】‎ 命题q：函数在上递增,若为真，而为假，求实数a的取值范围 ‎22. （12分）已知椭圆C:（a＞b＞0）的一个顶点为A （2,0），离心率为 ， 直线与椭圆C交与不同的两点M,N ‎(1)求椭圆C的方程；‎ ‎(2)当△AMN的面积为 时，求k的值.【来源：全,品…中&高*考+网】‎ 高二数学第二次月考试题答案(文)‎ 一 选择题 ‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ D C【来源：全,品…中&高*考+网】‎ A D D A A C B B B A 二、填空题 ‎13. 至少存在一个末位数字是0或5的整数不能被5整除 ‎14．解析：由双曲线的渐近线方程为 ‎15. ‎ ‎16.②③‎ 三、解答题17．(10分)求与椭圆＋＝1有公共焦点，并且离心率为的双曲线方程．‎ 解：由椭圆方程＋＝1，知长半轴a1＝3，短半轴b1＝2，焦距的一半c1＝＝，∴焦点是F1(－，0)，F2(，0)，因此双曲线的焦点也是F1(－，0)，F2(，0)，设双曲线方程为－＝1(a>0，b>0)，由题设条件及双曲线的性质，得解得故所求双曲线的方程为－y2＝1.‎ ‎18. 【答案】(1)由茎叶图知:分数在[50,60)之间的频数为2.‎ 由频率分布直方图知:分数在[50,60)之间的频率为0.008×10=0.08.‎ ‎∴全体女生的人数为=25人.‎ ‎(2)∵分数在[80,90)之间的人数为25﹣2﹣7﹣10﹣2=4人 ‎∴分数在[80,90)之间的频率为=0.16,‎ ‎∴频率分布直方图中[80,90)间的矩形的高为=0.016.‎ ‎(3)将[80,90)之间的4个分数编号为1,2,3,4；‎ ‎[90,100]之间的2个分数编号为5,6.‎ 则在[80,100]之间的试卷中任取两份的基本事件为:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共15个.【来源：全,品…中&高*考+网】‎ 至少有一个在[90,100]之间的基本事件有(1,5)(1,6)(2,5)(2,6)(3,5)(3,6)(4,5)(4,6)(5,6)共9个,‎ ‎∴至少有一份分数在[90,100]之间的概率是.‎ ‎19.⑴ ；⑵‎ ‎20. ‎ ‎21．(12)命题p：关于x的不等式对一切恒成立； ‎ 命题q：函数在上递增,若为真，而为假，求实数的取值范围 解：命题p：关于x的不等式对一切恒成立；‎ pT，即 命题q：函数在上递增；qT ‎∵为真，而为假，∴pq一真一假 p真q假时，pT；qF;∴‎ p假q真时，pF；qF;∴‎ ‎22.已知椭圆C：+=1（a＞b＞0）的一个顶点为A （2,0），离心率为， 直线y=k(x-1)与椭圆C交与不同的两点M,N ‎(1)求椭圆C的方程；‎ ‎(2)当△AMN的面积为时，求k的值.‎ ‎【答案】(1)由题意得解得.所以椭圆C的方程为.‎ ‎(2)由得.‎ 设点M,N的坐标分别为，，则，，，.‎ 所以|MN|===.‎ 由因为点A(2,0)到直线的距离，‎ 所以△AMN的面积为. 由，解得.‎