- 2021-06-16 发布 |
- 37.5 KB |
- 11页
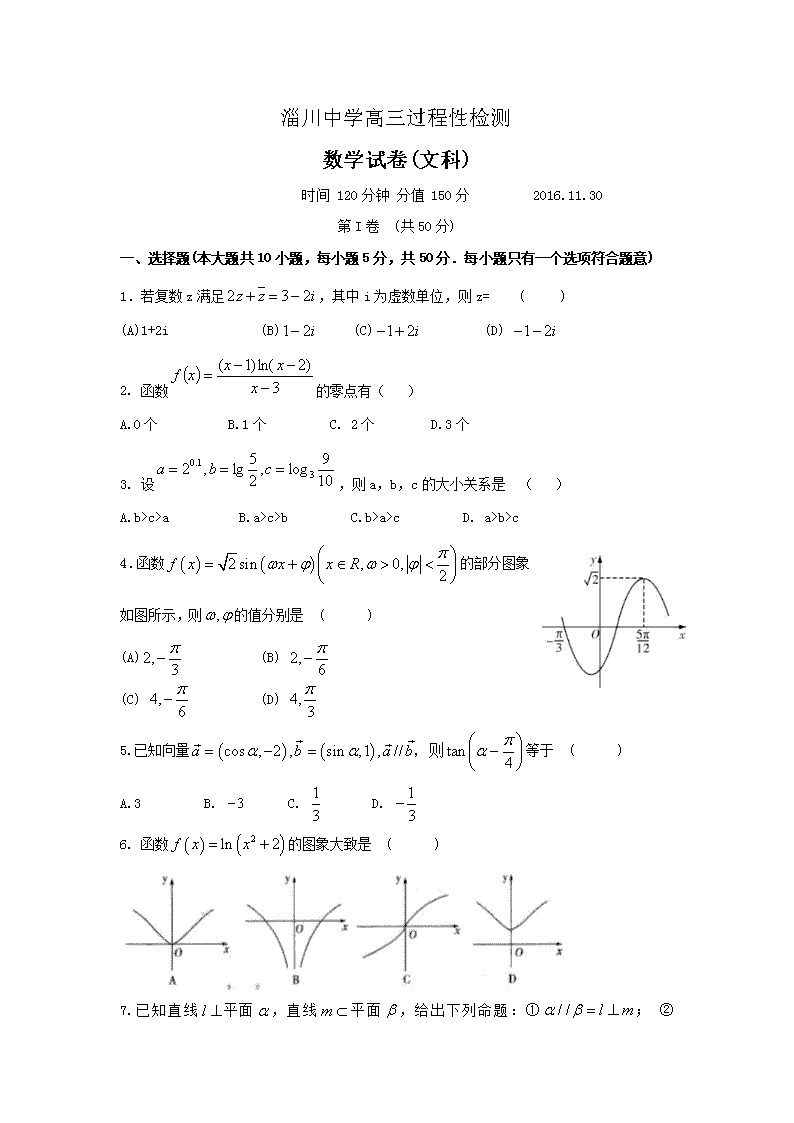


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文卷·2017届山东省淄博市淄川第一中学高三上学期第二次月考(2016
淄川中学高三过程性检测 数学试卷(文科) 时间 120分钟 分值 150分 2016.11.30 第I卷 (共50分) 一、选择题(本大题共10小题,每小题5分,共50分.每小题只有一个选项符合题意) 1.若复数z满足,其中i为虚数单位,则z= ( ) (A)1+2i (B) (C) (D) 2. 函数的零点有( ) A.0个 B.1个 C. 2个 D.3个 3. 设,则a,b,c的大小关系是 ( ) A.b>c>a B.a>c>b C.b>a>c D. a>b>c 4.函数的部分图象如图所示,则的值分别是 ( ) (A) (B) (C) (D) 5.已知向量等于 ( ) A.3 B. C. D. 6. 函数的图象大致是 ( ) 7.已知直线平面,直线平面,给出下列命题:①; ② ;③; ④.其中正确命题的序号是 ( ) (A)①②③ (B)②③④ (C)①③ (D)②④ 8.已知函数的图象与轴的两个相邻交点的距离等于,若将函数的图象向左平移个单位得到函数的图象,则在下列区间中使是减函数的是 ( ) (A) (B) (C) (D) 9. 已知是满足,且使取得最小值的正实数.若曲线过点,则的值为( ) A. 3 B.2 C. D.-1 10. 已知函数f(x)的定义域为R.当x<0时,f(x)=x3-1;当-1≤x≤1时,f(-x)= —f(x);当x>时,f(x+)=f(x—).则f(6)= ( ) A.-2 B.-1 C.0 D.2 第II卷(非选择题,共100分) 二、填空题(本大题共5个小题,每小题5分,共25分) 11. 12. 为了均衡教育资源,加大对偏远地区的教育投入,调查了某地若干户家庭的年收入x(单位:万元)和年教育支出y(单位:万元),调查显示年收入x与年教育支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程:.由回归直线方程可知,家庭年收入每增加1万元,年教育支出平均增加____________万元. 13.___________. 14.设D为所在平面内一点,,则 ____________. 15.如图,三棱锥平面ABC,AB=6,BC=12,AC=,SB=,则三棱锥S—ABC外接球的表面积为___________。 三、解答题 (本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤) 16. (本小题满分12分) 已知. (I)若的充分条件,求实数m的取值范围; (II)若,“p或q”为真命题,“p且q”为假命题,求实数x的取值范围. 17.(本小题满分12分) 对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: (I)求出表中M,p及图中a的值; (II)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求两人来自同一小组的概率. 18.(本小题满分l2分) 在△ABC中,内角A,B,C所对的边分别为已知. (I)若,求角A; (II)在(I)的条件下,若的面积为,求的值。 第19题图 19. (本小题满分12分) 已知在如图的多面体中,⊥底面,, ,是的中点. (1)求证:平面; (2)求证:平面. 20.(本小题满分13分)已知等差数列是方程的前n项和为 (I)求数列,的通项公式; (II)设数列满足,的前n项和 21、(本小题满分14分)已知函数. (I)当a=2时,求函数的单调区间; (II)当在定义域内的极值点; (III)成立,求实数a的取值范围. 18(本小题满分12分) 如图,四棱锥P—ABCD中,PA底面ABCD,AD//BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点. (I)证明MN//平面PAB; (11)求四面体N—BCM的体积. 20. (本小题满分12分) 第20题图 已知在如图的多面体中,⊥底面,, ,是的中点. (1)求证:平面; (2)求证:平面. 19.如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面底面ABCD,且,若E,F分别为PC,BD的中点. (I)求证:EF//平面PAD; (II)求三棱锥F-DEC的体积; (19)(本小题满分12分) 设等差数列的前项和为,且. (I)求数列的通项公式; (Ⅱ)设数列满足的前项和. (21)(本小题满分12分) 已知函数. (I)若是函数的极大值点,求函数的单调递减区间; (Ⅱ)若恒成立,求实数的最大值. (6)若三条直线相交于同一点,则点(m,n)到原点的距离的最小值为 (A) (B) (C) (D) (8)《莱因德纸草书》是世界上最古老的数学著作之一。书中有一道这样的题目:把100个面包分给五个人,使每人所得成等差数列,且使较大的三份之和的是较小的两份之和,问最小1份为 (A) (B) (C) (D) (9)若实数x,y满足不等式组的最小值等于,则实数m的值等于 (A)-1 (B)1 (C)-2 (D)2 BADAB DCDCD 查看更多