【数学】2018届一轮复习人教A版二次函数与幂函数教案
1.掌握二次函数的图象与性质(单调性、对称性、顶点、最值).
2.了解二次函数的广泛应用.
3.了解幂函数的概念.
4.结合函数y=x,y=x2,y=x3,y=,y=x的图象,了解它们的变化情况.
知识点一 幂函数
1.幂函数的定义
形如________(α∈R)的函数称为幂函数,其中x是________,α为______.
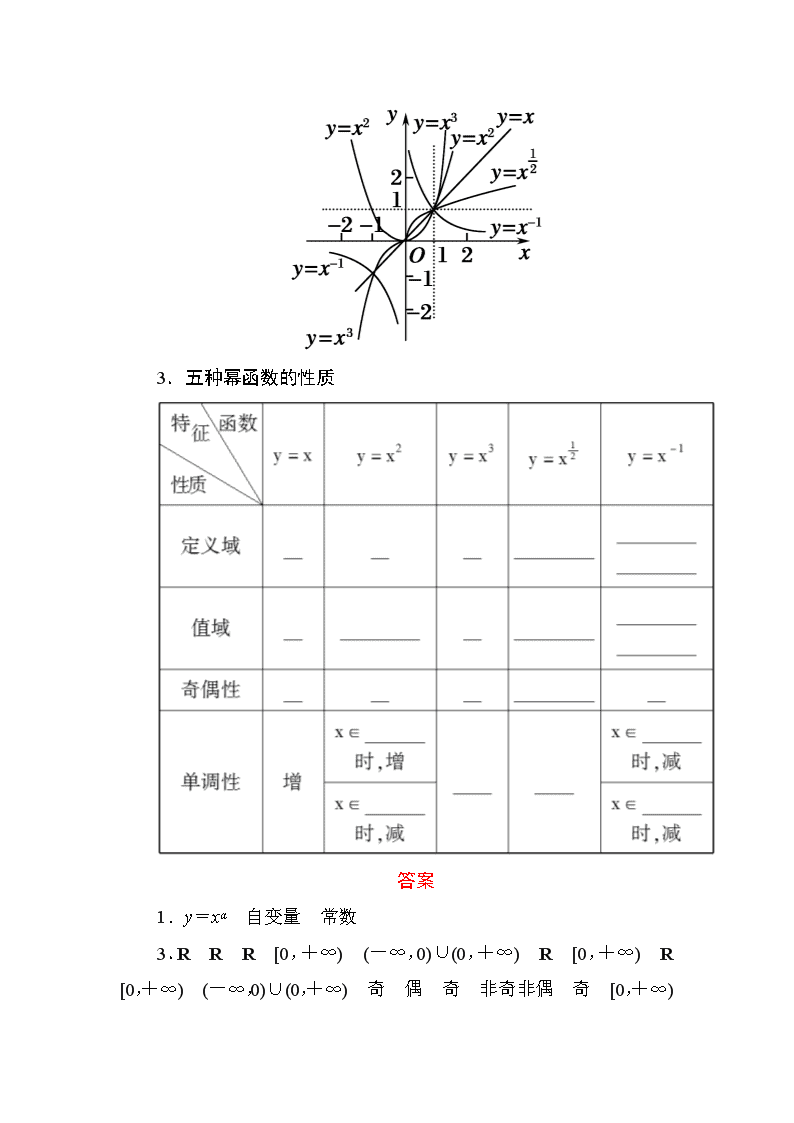
2.五种幂函数的图象
3.五种幂函数的性质
答案
1.y=xα 自变量 常数
3.R R R [0,+∞) (-∞,0)∪(0,+∞) R [0,+∞) R [0,+∞) (-∞,0)∪(0,+∞
) 奇 偶 奇 非奇非偶 奇 [0,+∞) (-∞,0] 增 增 (0,+∞) (-∞,0)
1.判断正误
(1)函数f(x)=x2与函数f(x)=2x2都是幂函数.( )
(2)幂函数的图象都经过点(1,1)和(0,0).( )
(3)幂函数的图象不经过第四象限.( )
答案:(1)× (2)× (3)√
2.(必修①P82A组第10题改编)已知幂函数f(x)=k·xα的图象过点,则k+α=( )
A. B.1
C. D.2
解析:因为f(x)=k·xα是幂函数,所以k=1.又f(x)的图象过点,所以α=,所以α=,所以k+α=1+=.
答案:C
知识点二 二次函数
1.二次函数的三种常见解析式
(1)一般式:f(x)=ax2+bx+c(a≠0);
(2)顶点式:f(x)=a(x-m)2+n(a≠0),(m,n)为顶点坐标;
(3)两根式:f(x)=a(x-x1)(x-x2)(a≠0),其中x1,x2分别是f(x)=0的两实根.
2.二次函数的图象和性质
函数
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)
图象
a>0
a<0
定义域
R
R
值域
y∈____________
y∈____________
对称轴
x=________
顶点
坐标
奇偶性
b=0⇔y=ax2+bx+c(a≠0)是偶函数
递增
区间
递减
区间
答案
2. -
3.(必修①P24习题1.2A组第6题改编)若函数f(x)=x2+bx+c,且f(0)=0,f(3)=0,则f(-1)=( )
A.-1 B.-2
C.1 D.4
解析:由f(0)=0,f(3)=0,得解得所以f(x)=x2-3x,所以f(-1)=4,故选D.
答案:D
4.已知函数f(x)=ax2+x+5的图象在x轴上方,则a的取值范围是( )
A. B.
C. D.
解析:由题意知即得a>.
答案:C
5.已知函数y=x2-2x+3在闭区间[0,m]上有最大值3,最小值2,则m的取值范围为________.
解析:如图,由图象可知m的取值范围是[1,2].
答案:[1,2]
热点一 幂函数的图象与性质
【例1】 (1)幂函数y=f(x)的图象过点(4,2),则幂函数y=f(x
)的图象是( )
(2)当0
g(x)>f(x).
【答案】 (1)C (2)h(x)>g(x)>f(x)
【总结反思】
(1)幂函数解析式一定要设为y=xα(α
为常数)的形式;(2)可以借助幂函数的图象理解函数的对称性、单调性;(3)在比较幂值的大小时,必须结合幂值的特点,选择适当的函数,借助其单调性进行比较,准确掌握各个幂函数的图象和性质是解题的关键.
比较下列各组数的大小:
(1)1.1,0.9,1;
(2) ,,(-1.1) .
解:(1)把1看作1,幂函数y=x在(0,+∞)上是增函数.
∵0<0.9<1<1.1,∴0.9<1<1.1,即0.9<1<1.1.
(2)因为=,
==,
(-1.1) =(1.12) =1.21,
幂函数y=x在(0,+∞)上是增函数,且<<1.21.
∴<<(-1.1) .
热点二 二次函数的图象及应用
【例2】 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出下面四个结论:
①b2>4ac;②2a-b=1;③a-b+c=0;④5a0,即b2>4ac,①正确;
对称轴为x=-1,即-=-1,2a-b=0,②错误;
结合图象,当x=-1时,y>0,即a-b+c>0,③错误;
由对称轴为x=-1知,b=2a.又函数图象开口向下,所以a<0,所以5a<2a,即5a0且a≠1)与二次函数y=(a-1)x2-x在同一坐标系内的图象可能是( )
解析:若01,则y=logax单调递增,y=(a-1)x2-x开口向上,其图象的对称轴在y轴右侧,排除B.故选A.
答案:A
热点三 二次函数的性质及应用
考向1 二次函数的单调性问题
【例3】 已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
(2)当a=1时,求f(|x|)的单调区间.
【解】 (1)由于函数f(x)的图象开口向上,对称轴是x=-a,所以要使f(x)在[-4,6]上是单调函数,应有-a≤-4或-a≥6,即a≤-6或a≥4.
所以实数a的取值范围是(-∞,-6]∪[4,+∞).
(2)当a=1时,f(x)=x2+2x+3,
∴f(|x|)=x2+2|x|+3,此时定义域为x∈[-6,6].
且f(x)=∴f(|x|)的单调递增区间是(0,6],单调递减区间是[-6,0].
考向2 二次函数的最值问题
【例4】 已知函数f(x)=-x2+2ax+1-a在x∈[0,1]时有最大值2,求a的值.
【解】 函数f(x)=-x2+2ax+1-a=-(x-a)2+a2-a+1,对称轴方程为x=a.
当a<0时,f(x)max=f(0)=1-a,
∴1-a=2,∴a=-1.
当0≤a≤1时,f(x)max=f(a)=a2-a+1.
∴a2-a+1=2,即a2-a-1=0.
∴a=(舍去).
当a>1时,f(x)max=f(1)=a,∴a=2.
综上可知,a=-1或a=2.
考向3 二次函数中的恒成立问题
【例5】 已知a是实数,函数f(x)=2ax2+2x-3在x∈[-1,1]上恒小于零,求实数a的取值范围.
【解】 由题意知2ax2+2x-3<0在[-1,1]上恒成立,
当x=0时,-3<0,适合;
当x≠0时,a<2-,
因为∈(-∞,-1]∪[1,+∞),当x=1时,右边取最小值,所以a<.
综上,实数a的取值范围是.
【总结反思】
1.二次函数最值问题的三种类型及解题思路
(1)类型:①对称轴、区间都是给定的;②对称轴动、区间固定;③对称轴定、区间变动.
(2)思路:抓“三点一轴”,三点是指区间两个端点和中点,一轴指的是对称轴.
2.由不等式恒成立求参数取值范围的两大思路及一个关键
(1)两大思路:一是分离参数;二是不分离参数.
(2)一个关键:两种思路都是将问题归结为求函数的最值,至于用哪种方法,关键是看参数是否已分离.这两个思路的依据是:a≥f(x)⇔a≥f(x)max,a≤f(x)⇔a≤f(x)min.
(1)(2017·宜春模拟)已知函数y=ax2+bx+c,如果a>b>c,且a+b+c=0,则它的图象是( )
(2)(2017·定州模拟)已知函数f(x)=-x2+4x在区间[-1,n]上的值域是[-5,4],则n的取值范围是( )
A.[2,5] B.[1,5]
C.[-1,2] D.[0,5]
(3)(2017·开封模拟)已知f(x)=x2+2(a-2)x+4,如果对x∈[-3,1],f(x)>0恒成立,则实数a的取值范围为____
.
解析:(1)因为a>b>c,且a+b+c=0,得a>0,且c<0,所以f(0)=c<0,所以函数y=ax2+bx+c的图象开口向上,与y轴的交点在y轴的负半轴上.
(2)f(x)=-x2+4x=-(x-2)2+4,
所以f(2)=4,又由f(x)=-5,得x=-1或5.
由f(x)的图象知:2≤n≤5.
(3)因为f(x)=x2+2(a-2)x+4,
对称轴x=-(a-2),
对x∈[-3,1],f(x)>0恒成立,所以讨论对称轴与区间[-3,1]的位置关系得:
或
或解得a∈∅或1≤a<4或-
查看更多