2020-2021学年高一数学单元知识梳理：集合与常用逻辑用语

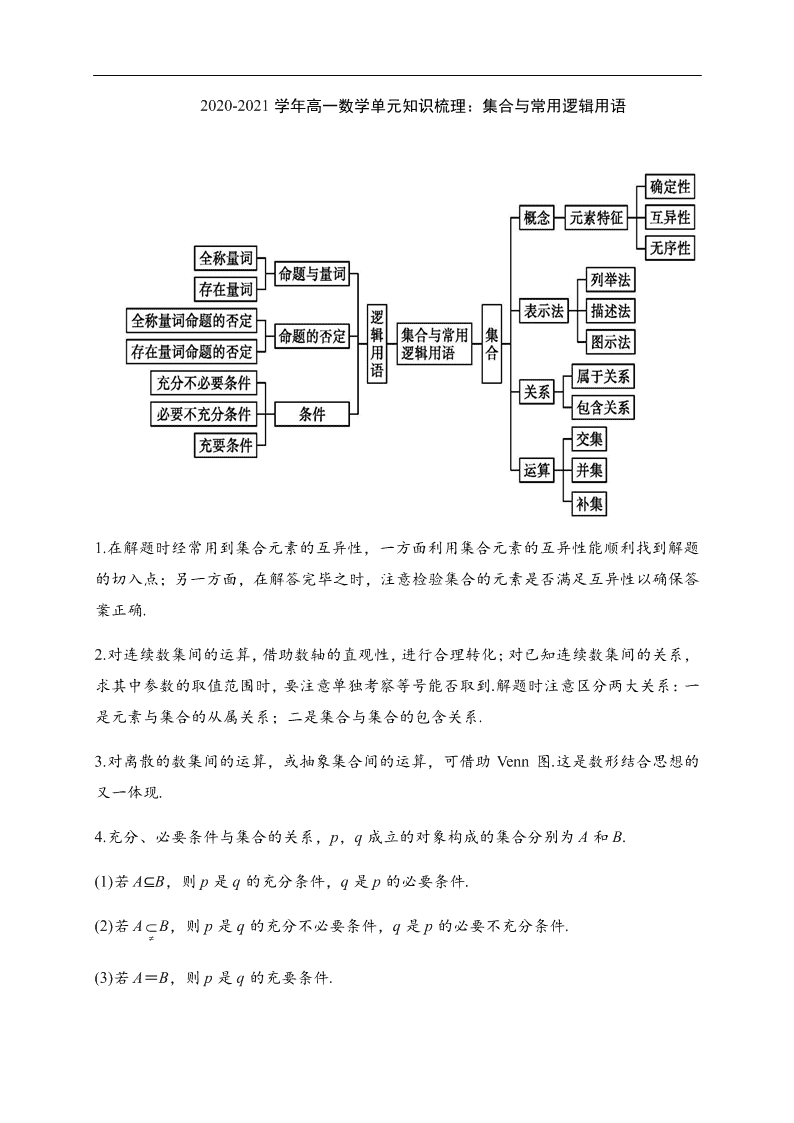
2020-2021学年高一数学单元知识梳理：集合与常用逻辑用语

2020-2021 学年高一数学单元知识梳理：集合与常用逻辑用语 1.在解题时经常用到集合元素的互异性，一方面利用集合元素的互异性能顺利找到解题 的切入点；另一方面，在解答完毕之时，注意检验集合的元素是否满足互异性以确保答 案正确. 2.对连续数集间的运算，借助数轴的直观性，进行合理转化；对已知连续数集间的关系， 求其中参数的取值范围时，要注意单独考察等号能否取到.解题时注意区分两大关系：一 是元素与集合的从属关系；二是集合与集合的包含关系. 3.对离散的数集间的运算，或抽象集合间的运算，可借助 Venn 图.这是数形结合思想的 又一体现. 4.充分、必要条件与集合的关系，p，q 成立的对象构成的集合分别为 A 和 B. (1)若 A⊆B，则 p 是 q 的充分条件，q 是 p 的必要条件. (2)若 A   B，则 p 是 q 的充分不必要条件，q 是 p 的必要不充分条件. (3)若 A＝B，则 p 是 q 的充要条件. 5.判断条件之间的关系要注意条件之间关系的方向，正确理解“p 的一个充分而不必要 条件是 q”等语言. 6.要写一个命题的否定，需先分清其是全称命题还是特称命题，再对照否定结构去写， 并注意与否命题的区别；否定的规律是“改量词，否结论”. 一、数学抽象 数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养．主要表现为：获得数 学概念和规则，提出数学命题和模型，形成数学方法和思想，认识数学结构与体系．在本章中，主 要表现在集合概念的理解及应用中. 【典例 1】(1)已知集合 A＝{0，1，2}，则集合 B＝{x－y|x∈A，y∈A}中元素的个数是( ) A．1 B．3 C．5 D．9 (2)若－3∈{x－2，2x2＋5x，12}，则 x＝________． 【答案】(1)C (2)－ 2 3 【解析】(1)①当 x＝0 时，y＝0，1，2，此时 x－y 的值分别为 0，－1，－2； ②当 x＝1 时，y＝0，1，2，此时 x－y 的值分别为 1，0，－1； ③当 x＝2 时，y＝0，1，2，此时 x－y 的值分别为 2，1，0. 综上可知，x－y 的可能取值为－2，－1，0，1，2，共 5 个，故选 C. (2)由题意知，x－2＝－3 或 2x2＋5x＝－3. ①当 x－2＝－3 时，x＝－1. 把 x＝－1 代入，得集合的三个元素为－3，－3，12，不满足集合中元素的互异性； ②当 2x2＋5x＝－3 时，x＝－ 或 x＝－1(舍去)， 当 x＝－ 时，集合的三个元素为－ 2 7 ，－3，12，满足集合中元素的互异性，由①②知 x＝－ . 二、数学运算 数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养，主要表现为：理解运 算对象，掌握运算法则，探究运算思路，求得运算结果．在本章中，主要表现在集合的交、并、补 运算中. 【典例 2】(1)设集合 A＝{1，2，4}，B＝{x|x2－4x＋m＝0}．若 A∩B＝{1}，则 B＝( ) A．{1，－3} B．{1，0} C．{1，3} D．{1，5} (2)若集合 A＝{x|－2＜x＜1}，B＝{x|x＜－1 或 x＞3}，则 A∩B＝( ) A．{x|－2＜x＜－1} B．{x|－2＜x＜3} C．{x|－1＜x＜1} D．{x|1＜x＜3} 【答案】(1)C (2)A 【解析】(1)由 A∩B＝{1}得 1∈B， 所以 m＝3，B＝{1，3}． (2)A∩B＝{x|－2＜x＜－1}． (3)已知集合 A＝{x|2≤x＜7}，B＝{x|3＜x＜10}，C＝{x|x＜a}． ①求 A∪B，(∁RA)∩B； ②若 A∩C≠∅，求 a 的取值范围． 【解析】①因为 A＝{x|2≤x＜7}，B＝{x|3＜x＜10}， 所以 A∪B＝{x|2≤x＜10}． 因为 A＝{x|2≤x＜7}， 所以∁RA＝{x|x＜2 或 x≥7}， 则(∁RA)∩B＝{x|7≤x＜10}． ②因为 A＝{x|2≤x＜7}，C＝{x|x＜a}，且 A∩C≠∅，所以 a＞2， 所以 a 的取值范围是{a|a＞2}． 三、逻辑推理 逻辑推理是指从一些事实和命题出发，依据规则推出其他命题的素养，主要表现为：掌握推理基本 形式和规则，发现问题和提出问题，探索和表述论证过程，理解命题体系，有逻辑地表达与交流．本 章主要表现在集合的基本关系、充要条件及全称量词命题和存在量词命题中. 【典例 3】(1)集合 A＝{x|x＝a2－4a＋5，a∈R}，B＝{y|y＝4b2＋4b＋3，b∈R}，则下列关系正确的是 ( ) A．A＝B B．B   A C．A⊆B D．B A (2)已知集合 A＝{x|0＜x＜4}，B＝{x|x＜a}，若 A⊆B，则实数 a 的取值范围是( ) A．{a|0＜a＜4} B．{a|－8＜a＜4} C．{a|a≥4} D．{a|a＞4} 【答案】(1)B (2)C 【解析】(1)A＝{x|x＝(a－2)2＋1，a∈R}，即 A 中的元素 x≥1；而 B＝{y|y＝(2b＋1)2＋2，b∈R}，即 B 中的元素 y≥2，∴B A. (2)在数轴上标出 A，B 两集合如图所示， 结合数轴知，若 A⊆B，则 a≥4. 【典例 4】设 x∈R，则“2－x≥0”是“－1≤x－1≤1”的( ) A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 【答案】B 【解析】由－1≤x－1≤1，得 0≤x≤2，因为 0≤x≤2⇒x≤2，x≤2 0≤x≤2，故“2－x≥0”是 “－1≤x－1≤1”的必要不充分条件，故选 B. 【典例 5】若 a，b 都是实数，试从①ab＝0；②a＋b＝0；③a(a2＋b2)＝0；④ab＞0 中选出满足下列 条件的式子，用序号填空： (1)使 a，b 都为 0 的必要条件是________； (2)使 a，b 都不为 0 的充分条件是________； (3)使 a，b 至少有一个为 0 的充要条件是________． 【答案】(1)①②③ (2)④ (3)①8 【解析】①ab＝0⇔a＝0 或 b＝0，即 a，b 至少有一个为 0； ②a＋b＝0⇔a，b 互为相反数，则 a，b 可能均为 0，也可能为一正数一负数； ③a(a2＋b2)＝0⇔a＝0，b 为任意实数； ④ab＞0⇔      0 0 b a 或      0 0 b a 即 a，b 同为正数或同为负数． 综上可知：(1)使 a，b 都为 0 的必要条件是①②③； (2)使 a，b 都不为 0 的充分条件是④； (3)使 a，b 至少有一个为 0 的充要条件是①. 【典例 6】已知集合 A＝{x∈R|2x＋m＜0}，B＝{x∈R|x＜－1 或 x＞3}． (1)是否存在实数 m，使得 x∈A 是 x∈B 成立的充分条件？ (2)是否存在实数 m，使得 x∈A 是 x∈B 成立的必要条件？ 【解析】(1)欲使 x∈A 是 x∈B 成立的充分条件， 则只要 }2{ mxx  ⊆{x|x＜－1 或 x＞3}，则只要－ 2 m ≤－1 即 m≥2， 故存在实数 m≥2 时使 x∈A 是 x∈B 成立的充分条件． (2)欲使 x∈A 是 x∈B 成立的必要条件， 则只要 ⊇{x|x＜－1 或 x＞3}，则这是不可能的，故不存在实数 m，使 x∈A 是 x∈B 成立 的必要条件. 【典例 7】判断下列命题是全称量词命题还是存在量词命题，判断真假 ，并写出它们的否定： (1)空集是任何一个非空集合的真子集． (2)∀x∈R，4x2＞2x－1＋3x2. (3)∃x∈{－2，－1，0，1，2}，|x－2|＜2. (4)∀a，b∈R，方程 ax＋b＝0 恰有一解． 【解析】(1)该命题是全称量词命题，是真命题．该命题的否定：存在一个非空集合，空集不是该集 合的真子集． (2)该命题是全称量词命题，是假命题． 因为 4x2－(2x－1＋3x2)＝x2－2x＋1＝(x－1)2≥0， 所以当 x＝1 时，4x2＝2x－1＋3x2. 该命题的否定：∃x∈R，4x2≤2x－1＋3x2. (3)该命题是存在量词命题，是真命题． 因为当 x＝1 时，|x－2|＝1＜2. 该命题的否定：∀x∈{－2，－1，0，1，2}，|x－2|≥2. (4)该命题是全称量词命题，是假命题．当 a≠0 时，方程 ax＋b＝0 才恰有一解．该命题的否定：∃a， b∈R，方程 ax＋b＝0 无解或至少有两解． 四、数学建模 数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养， 主要表现在：发现和提出问题，建立和求解模型，检验和完善模型，分析和解决问题，在本章主要 表现在集合的实际应用问题中. 【典例 8】某班有 36 名同学参加数学、物理、化学课外探究小组，每名同学至多参加两个小组，已 知参加数学、物理、化学小组的人数分别为 26，15，13，同时参加数学和物理小组的有 6 人，同时 参加物理和化学小组的有 4 人，则同时参加数学和化学小组的有________人． 【答案】8 【解析】设参加数学、物理、化学小组的人数构成的集合分别为 A，B，C，同时参加数学和化学小 组的有 x 人，由题意可得如图所示的 Venn 图． 由全班共 36 名同学可得(26－6－x)＋6＋(15－4－6)＋4＋(13－4－x)＋x＝36， 解得 x＝8，即同时参加数学和化学小组的有 8 人．