用样本的频率分布估计总体分布2

用样本的频率分布估计总体分布2

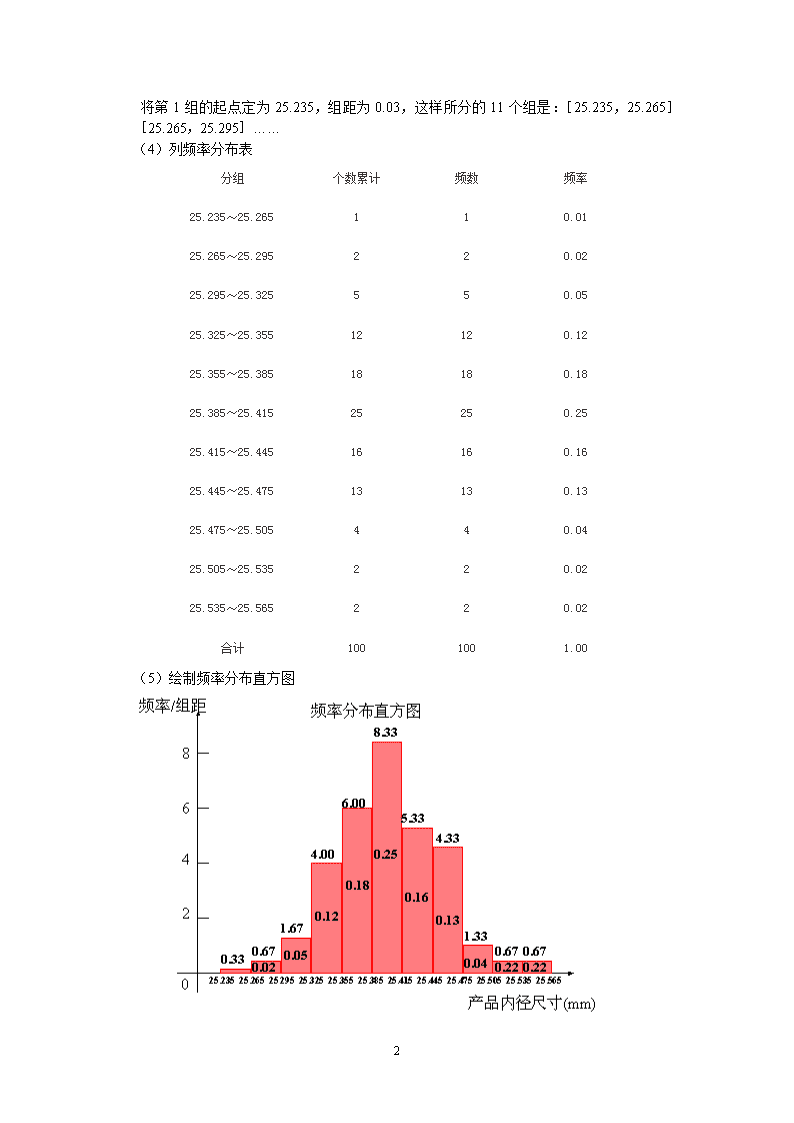
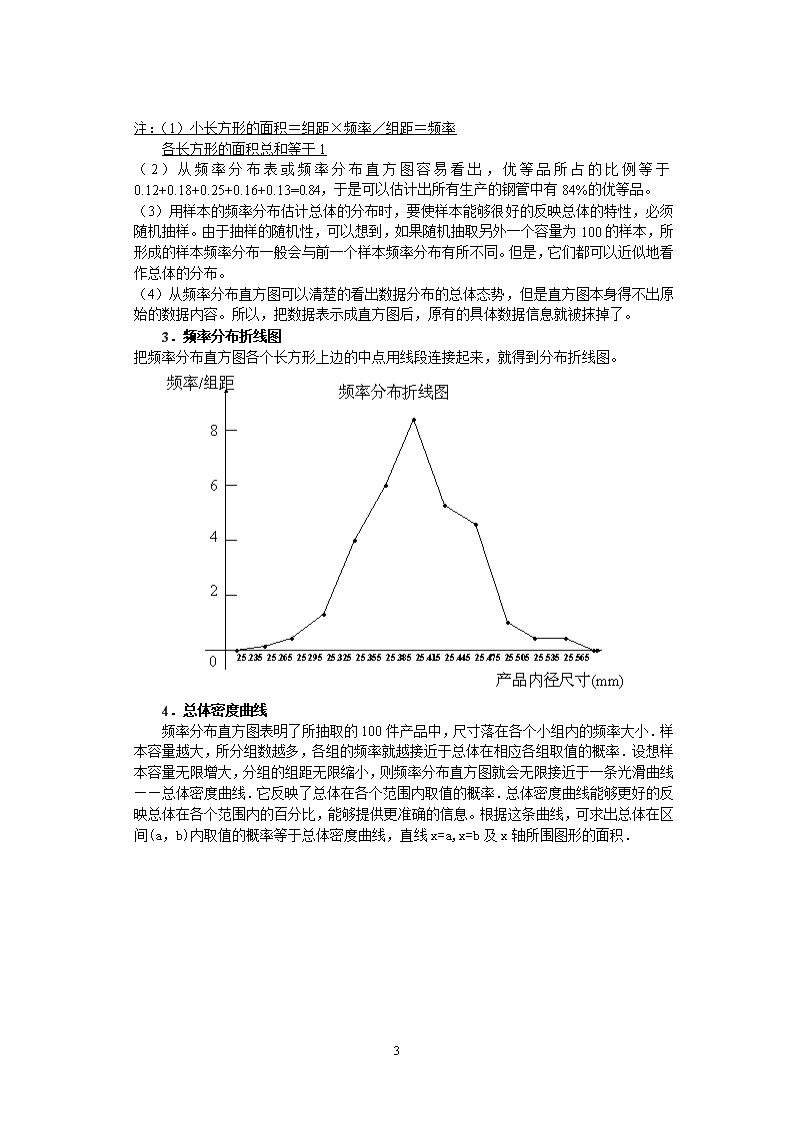
‎ ‎ ‎2．2．1 用样本的频率分布估计总体的分布 荣成二中 宋海燕 目的要求 ‎ 通过实例体会分布的意义和作用，在表示数据的过程中，学会列出频率分布表、画频率分布直方图、频率折线图、茎叶图，体会它们各自的特点。‎ ‎ 教学过程 ‎ 1．实例引课 ‎ 为了解某地区女中学生的身体发育情况，不仅要了解其平均身高，还要了解身高在哪个范围内的学生多，哪个范围内的学生少．‎ 为了解某次考试成绩，不仅应知道平均成绩，还应知道90分以上占多少，80分～90分占多少，……，不及格占多少等．‎ 要解决上面的两个问题，需要从总体中得到一个包含大量数据的样本，并且把这些数据形成频率分布，就可以比较清楚地看出样本数据的特征，从而估计总体的分布情况。‎ ‎ 2．引出课题：用样本的频率分布估计总体的分布 ‎ 看下面的例子 某钢铁加工厂生产内径为25．40mm的钢管，为了掌握产品的生产状况，需要定期对产品进行检测。又由于产品的数量巨大，不可能一一检测所有的钢管，因而通常采用随机抽样的办法。如果把这些钢管的内径看成总体，我们可以从中随机抽取的100件钢管进行检测，把这100件钢管的质量分布情况作为总体的质量分布情况来看待。根据规定，钢管内径的尺寸在区间25.325～25.475内为优等品，我们特别希望知道所有生产的钢管中优等品所占的比例，这时就可以用样本的分布情况估计总体的分布情况。‎ 下面的数据是一次抽样中的100件钢管的内径尺寸：(幻灯示)．‎ ‎25.39 25.36 25.34 25.42 25.45 25.38 25.39 25.42 25.47 25.35‎ ‎25.41 25.43 25.44 25.48 25.45 25.43 25.46 25.40 25.51 25.45‎ ‎25.40 25.39 25.41 25.36 25.38 25.31 25.56 25.43 25.40 25.38‎ ‎25.37 25.44 25.33 25.46 25.40 25.49 25.34 25.42 25.50 25.37‎ ‎25.35 25.32 25.45 25.40 25.27 25.43 25.54 25.39 25.45 25.43‎ ‎25.40 25.43 25.44 25.41 25.53 25.37 25.38 25.24 25.44 25.40‎ ‎25.36 25.42 25.39 25.46 25.38 25.35 25.31 25.34 25.40 25.36‎ ‎25.41 25.32 25.38 25.42 25.40 25.33 25.37 25.41 25.49 25.35‎ ‎25.47 25.34 25.30 25.39 25.36 25.46 25.29 25.40 25.37 25.33‎ ‎25.40 25.35 25.41 25.37 25.47 25.39 25.42 25.47 25.38 25.39‎ ‎ 上面的100个数据有点散乱，从中很难看出产品质量的分布情况，必须对样本数据用统计的方法加以概括和整理。下面我们列出这组样本数据的频率分布表、频率分布直方图，步骤如下：‎ ‎（1）计算级差（一组数据中最大值与最小值的差）‎ ‎ 25.26－25.24＝0.32‎ ‎（2）决定组距与组数（样本容量不超过100时，组数常分为5～12组）‎ 如果组距定为0.03，那么 ‎ 级差/组距＝0.32/0.03＝10 2/3‎ 于是应将样本数据分成11组（组距还可以定为其他的数值）‎ ‎（3）决定分点 6‎ ‎ ‎ ‎ 将第1组的起点定为25.235，组距为0.03，这样所分的11个组是：［25.235，25.265］［25.265，25.295］……‎ ‎（4）列频率分布表 分组 个数累计 频数 频率 ‎25.235～25.265‎ ‎1‎ ‎1‎ ‎0.01‎ ‎25.265～25.295‎ ‎2‎ ‎2‎ ‎0.02‎ ‎25.295～25.325‎ ‎5‎ ‎5‎ ‎0.05‎ ‎25.325～25.355‎ ‎12‎ ‎12‎ ‎0.12‎ ‎25.355～25.385‎ ‎18‎ ‎18‎ ‎0.18‎ ‎25.385～25.415‎ ‎25‎ ‎25‎ ‎0.25‎ ‎25.415～25.445‎ ‎16‎ ‎16‎ ‎0.16‎ ‎25.445～25.475‎ ‎13‎ ‎13‎ ‎0.13‎ ‎25.475～25.505‎ ‎4‎ ‎4‎ ‎0.04‎ ‎25.505～25.535‎ ‎2‎ ‎2‎ ‎0.02‎ ‎25.535～25.565‎ ‎2‎ ‎2‎ ‎0.02‎ 合计 ‎100‎ ‎100‎ ‎1.00‎ ‎（5）绘制频率分布直方图 6‎ ‎ ‎ 注：（1）小长方形的面积＝组距×频率／组距＝频率 各长方形的面积总和等于1‎ ‎（2）从频率分布表或频率分布直方图容易看出，优等品所占的比例等于0.12+0.18+0.25+0.16+0.13=0.84，于是可以估计出所有生产的钢管中有84%的优等品。‎ ‎（3）用样本的频率分布估计总体的分布时，要使样本能够很好的反映总体的特性，必须随机抽样。由于抽样的随机性，可以想到，如果随机抽取另外一个容量为100的样本，所形成的样本频率分布一般会与前一个样本频率分布有所不同。但是，它们都可以近似地看作总体的分布。‎ ‎（4）从频率分布直方图可以清楚的看出数据分布的总体态势，但是直方图本身得不出原始的数据内容。所以，把数据表示成直方图后，原有的具体数据信息就被抹掉了。‎ ‎3．频率分布折线图 把频率分布直方图各个长方形上边的中点用线段连接起来，就得到分布折线图。‎ ‎4．总体密度曲线 频率分布直方图表明了所抽取的100件产品中，尺寸落在各个小组内的频率大小．样本容量越大，所分组数越多，各组的频率就越接近于总体在相应各组取值的概率．设想样本容量无限增大，分组的组距无限缩小，则频率分布直方图就会无限接近于一条光滑曲线——总体密度曲线．它反映了总体在各个范围内取值的概率．总体密度曲线能够更好的反映总体在各个范围内的百分比，能够提供更准确的信息。根据这条曲线，可求出总体在区间(a，b)内取值的概率等于总体密度曲线，直线x=a,x=b及x轴所围图形的面积．‎ 6‎ ‎ ‎ ‎5．茎叶图 常用的统计图表还有茎叶图，下面的例子就是用茎叶图表示数据。‎ 例：某赛季甲、乙两名篮球运动员每场比赛的得分情况如下：‎ 甲的得分：12，15，24，25，31，31，36，36，37，39，44，49，50。‎ 乙的得分：8，13，14，16，23，26，28，33，38，39，51。‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎8‎ ‎346‎ ‎368‎ ‎389‎ ‎1‎ ‎52‎ ‎54‎ ‎976611‎ ‎94‎ ‎0‎ 甲 乙 注：中间的数字表示得分的十位数字。‎ 旁边的数字分别表示两个人得分的个位数字 从上面这个茎叶图上可以看出，甲运动员的得分情况是大致对称的，中位数是36；乙运动员的得分情况除一个特殊得分外，也大致对称，中位数是26。因此甲运动员的发挥比较稳定，总体得分情况比乙运动员好。‎ 用茎叶图表示数据有两个突出的优点，一是从统计图上没有原始信息的损失，所有的数据信息都可以从茎叶图中得到；二是茎叶图可以在比赛是随时记录，方便记录与表示。但茎叶图只便于表示两位有效数字的数据，虽然可以表示两个人以上的比赛结果（或两个以上的记录），但没有表示两个记录那么直观、清晰。‎ ‎6．课堂练习 ‎1)、对于样本频率分布直方图与总体密度曲线的关系，下列说法中正确的是（ ）‎ ‎（A）频率分布直方图与总体密度曲线无关 ‎（B）频率分布直方图就是总体密度曲线 ‎ 6‎ ‎ ‎ ‎（C）样本容量很大的频率分布直方图就是总体密度曲线 ‎ ‎（D）如果样本容量无限增大，分组的组距无限减小，那么频率分布直方图就会无限接近于总体密度曲线 ‎2)、在用样本频率估计总体分布的过程中，下列说法中正确的是（ ）‎ ‎（A）总体容量越大，估计越精确 　　（B）总体容量越小，估计越精确 ‎ ‎（C）样本容量越大，估计越精确 　　（D）样本容量越小，估计越精确 ‎3)、10个小球分别编有号码1，2，3，4，其中1号球4个，2号球2个，3号球3个，4号球1个，数0.4是指1号球占总体分布的（ ）‎ ‎（A）频数 　　（B）概率 　　（C）频率 　　（D）累计频率 ‎4)、已知样本：‎ ‎12 7 11 12 11 12 10 10 9 8 13 12 10 9 6 11 8 9 8 10那么频率为0.25的样本的范围是（ ）‎ ‎（A） 　　（B） 　　（C） 　　（D） ‎ ‎5)、频率分布直方图中，小长方体的面积等于（ ）‎ ‎（A）相应各组的频数 　　（B）相应各组的频率 　　（C）组数 　　（D）组距 ‎6)、在总体密度曲线中，总体在区间（a，b）内取值的概率就是直线______、_______、_______和总体密度曲线围成的图形的面积.‎ ‎7)、对100位大学毕业生在该年七月份求职录取情况调查结果如下：20人录取在行政机关，31人录取在公司，3人录取在银行，18人录取在学校，其余的还在求职中.那么七月份这100位大学生还未被录取的概率为_______________.‎ ‎8)、一个容量为n的样本分成若干组，已知某组的频数和频率分别为30和0.25，则n=_______________.‎ ‎　9)‎ ‎ 分 组 ‎ 频 数 ‎ 频 率 ‎ [10．75， 10．85）‎ ‎ 3‎ ‎ [10．85， 10．95）‎ ‎ 9‎ ‎ [10．95， 11．05）‎ ‎ 13‎ ‎ [11．05， 11．15）‎ ‎ 16‎ ‎ [11．15， 11．25）‎ ‎ 26‎ ‎ [11．25， 11．35）‎ ‎ 20‎ ‎ [11．35， 11．45）‎ ‎ 7‎ ‎ [11．45， 11．55）‎ ‎ 4‎ ‎ [11．55， 11．65）‎ ‎ 2‎ ‎ 合 计 ‎ 100‎ ‎ (1)完成上面的频率分布表．‎ 6‎ ‎ ‎ ‎ (2)根据上表，画出频率分布直方图．‎ ‎ (3)根据上表，估计数据落在[10．95，11．35)范围内的概率约为多少?‎ ‎ 解：(1)(2)略．‎ ‎ (3)数据落在[10．95，11．35]范围的频率为0．13+0．16十0．26+0．20‎ 落在[10．95，11．35]内的概率约为0．75．‎ ‎ 10）教科书第67页练习B第2、3题．‎ ‎7．归纳小结 ‎①获得样本的频率分布的步骤：‎ ‎(1)求最大值与最小值的差；(2)确定组距与组数；（3）决定分点；（4）列频率分布表；（5）绘制频率分布直方图.‎ ‎②‎ 图形 优点 缺点 频率分布直方图 ‎1）易表示大量数据 ‎2）直观的反映分布的情况 都是一些信息 茎叶图 ‎1）无信息损失 ‎2）随时记录，方便记录和表示 只能处理样本容量较小数据 ‎8．布置做业 教科书第69页练习A第3、4题 6‎