2018届二轮复习一道取材于生活的概率试题的分析与解学案（江苏专用）

2018届二轮复习一道取材于生活的概率试题的分析与解学案（江苏专用）

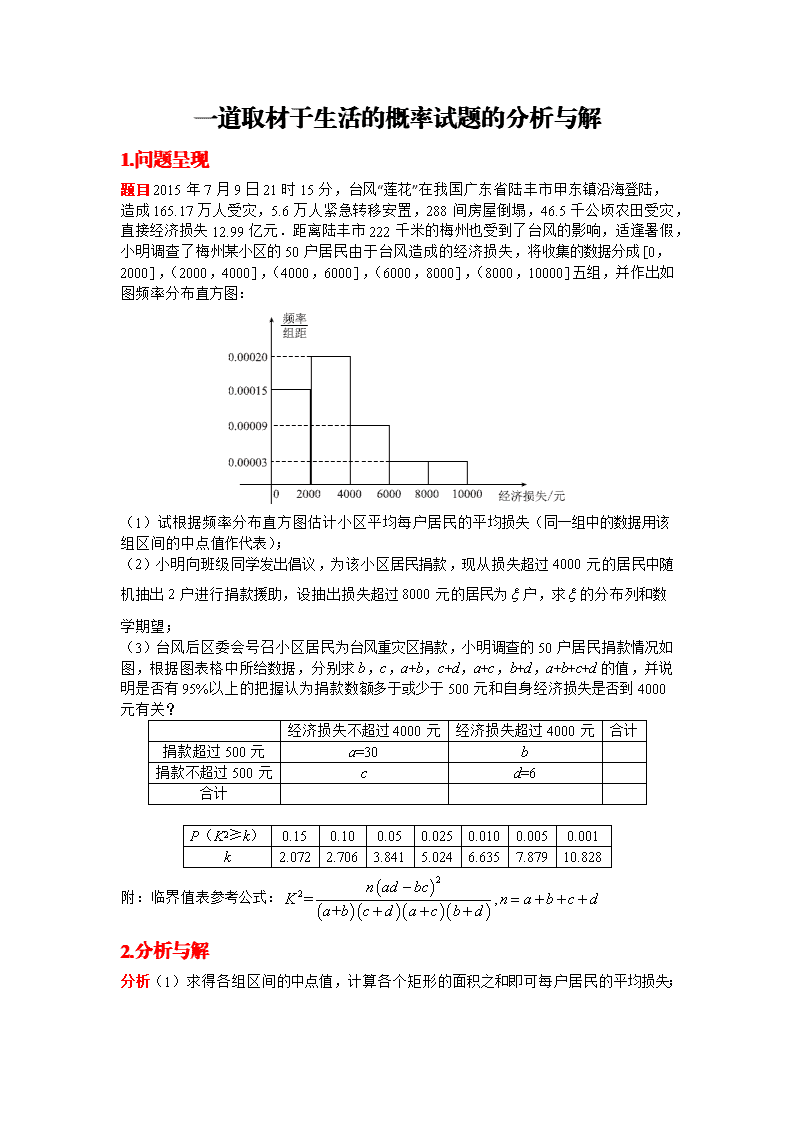
一道取材于生活的概率试题的分析与解 ‎1.问题呈现 ‎ 题目2015年7月9日21时15分，台风“莲花”在我国广东省陆丰市甲东镇沿海登陆，造成165.17万人受灾，5.6万人紧急转移安置，288间房屋倒塌，46.5千公顷农田受灾，直接经济损失12.99亿元．距离陆丰市222千米的梅州也受到了台风的影响，适逢暑假，小明调查了梅州某小区的50户居民由于台风造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出如图频率分布直方图：‎ ‎（1）试根据频率分布直方图估计小区平均每户居民的平均损失（同一组中的数据用该组区间的中点值作代表）；‎ ‎（2）小明向班级同学发出倡议，为该小区居民捐款，现从损失超过4000元的居民中随机抽出2户进行捐款援助，设抽出损失超过8000元的居民为户，求的分布列和数学期望；‎ ‎（3）台风后区委会号召小区居民为台风重灾区捐款，小明调查的50户居民捐款情况如图，根据图表格中所给数据，分别求b，c，a+b，c+d，a+c，b+d，a+b+c+d的值，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？‎ 经济损失不超过4000元 经济损失超过4000元 合计 捐款超过500元 a=30‎ b 捐款不超过500元 c d=6‎ 合计 P（K2≥k）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 附：临界值表参考公式：‎ ‎2.分析与解 ‎ 分析（1）求得各组区间的中点值，计算各个矩形的面积之和即可每户居民的平均损失；‎ ‎（2）由频率分布直方图可得，损失超过4000元的居民共有15户；损失超过8000元的居民共有3户，因此，可能取值为0，1，2，运用排列组合的知识，可得各自的概率，由期望公式计算即可得到；‎ ‎（3）由（2）可得a，b，c，d，运用临界值参考公式，求出，与临界值比较，即可有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关．‎ 解（1）记每户居民的平均损失为元，‎ 则=（1000×0.00015+3000×0.0002+5000×0.00009+7000×0.00003+9000×0.00003）×2000=3360‎ ‎（2）由频率分布直方图，可得超过4000元的居民共有（0.00009+0.00003+0.00003）×2000×50=15户，‎ 损失超过8000元的居民共有0.00003×2000×50=3户，‎ 因此，的可能值为0，1，2．‎ ‎，，‎ ‎∴的分布列为 ‎0‎ ‎1‎ ‎2‎ 数学期望 ‎（3）解得b=9，c=5，a+b=39，c+d=11，a+c=35，b+d=15，a+b+c+d=50，‎ ‎，‎ 所以有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关 评注 本题考查根据频率分布直方图求均值，以及随机分布的概率和期望的计算，考查独立性检验的概率情况，考查运算能力，属于中档题．‎ ‎3.举一反三 题1某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据，结果统计如下：‎ API ‎[0，50]‎ ‎(50，100]‎ ‎(100，150]‎ ‎(150，200]‎ ‎(200， 250]‎ ‎(250，300]‎ ‎>300‎ 空气 质量 优 良 轻微 污染 轻度 污染 中度 污染 中重 度污染 重度 污染 天数 ‎4‎ ‎13‎ ‎18‎ ‎30‎ ‎9‎ ‎11‎ ‎15‎ 若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染.完成下面2×2列联表，并判断在犯错误的概率不超过多少的前提下(或有多大把握)认为该市本年空气重度污染与供暖有关？‎ 非重度污染 重度污染 总计 供暖季 非供暖季 总计 ‎100‎ P（K2≥k）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 附：临界值表参考公式：‎ 解 根据以上数据得到如下列联表：‎ 非重度污染 重度污染 总计 供暖季 ‎22‎ ‎8‎ ‎30‎ 非供暖季 ‎63‎ ‎7‎ ‎70‎ 总计 ‎85‎ ‎15‎ ‎100‎ 的观测值.‎ 所以在犯错误的概率不超过0.05的前提下(或有95%的把握)认为空气重度污染与供暖有关.‎ 题2通过随机询问某校110名高中学生在购买食物时是否看营养说明，得到如下的列联表：‎ 性别与看营养说明列联表　单位：名 男 女 总计 看营养说明 ‎50‎ ‎30‎ ‎80‎ 不看营养说明 ‎10‎ ‎20‎ ‎30‎ 总计 ‎60‎ ‎50‎ ‎110‎ ‎(1)从这50名女生中按是否看营养说明采取分层抽样，抽取一个容量为5的样本，问样本中看与不看营养说明的女生各有多少名？‎ ‎(2)从(1)中的5名女生中随机选取两名作深度访谈，求选到看与不看营养说明的女生各一名的概率.‎ ‎(3)根据以上列联表，问在犯错误的概率不超过多少的前提下(或有多大把握)认为“性别与在购买食物时看营养说明”有关？‎ P（K2≥k）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 附：临界值表参考公式：‎ 解 (1)根据分层抽样可得：样本中看营养说明的女生有名，样本中不看营养说明的女生有名.‎ ‎(2)设5名女生中看营养说明的为a1，a2，a3，不看营养说明的为b1，b2，则从中随机抽取2名，分别为{a1，a2}，{a1，a3}，{a1，b1}，{a1，b2}，{a2，a3}，{a2，b1}，{a2，b2}，{a3，b1}，{a3，b2}，{b1，b2}，其中看与不看营养说明的女生各一名的基本事件有6个，故所求概率为.‎ ‎(3)根据题中的列联表得，‎ ‎，所以在犯错误的概率不超过0.01的前提下(或有99%的把握)认为该校高中学生“性别与在购买食物时看营养说明”有关.‎