2018届二轮复习8-5直线、平面垂直的判定与性质课件（全国通用）

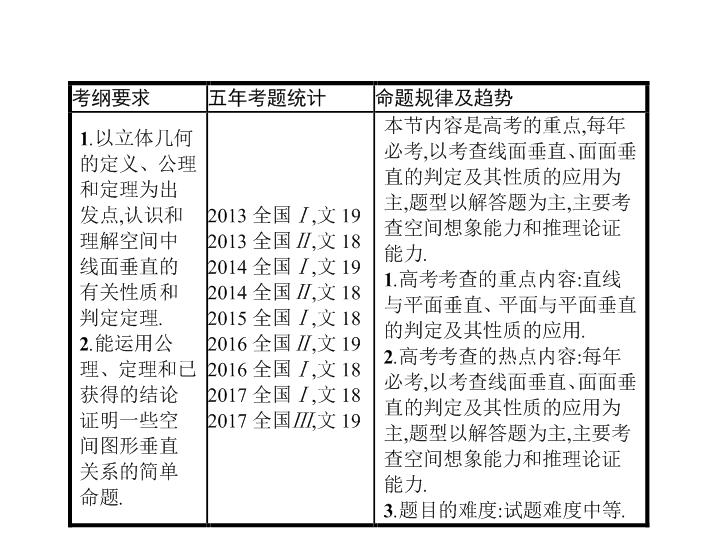
2018届二轮复习8-5直线、平面垂直的判定与性质课件（全国通用）

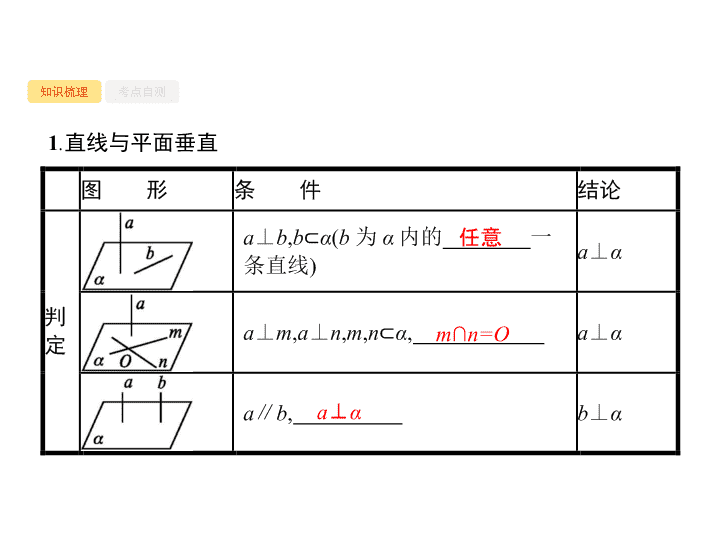
8 . 5 　 直线、平面垂直的判定与性质 - 2 - - 3 - 知识梳理 考点自测 1 . 直线与平面垂直 任意 m ∩ n=O a ⊥ α - 4 - 知识梳理 考点自测 b ⊂ α a ∥ b - 5 - 知识梳理 考点自测 2 . 平面与平面垂直 (1) 平面与平面垂直的定义 两个平面相交 , 如果它们所成的二面角是 　　　　　　　　 , 就说这两个平面互相垂直 .   (2) 判定定理与性质定理 直二面角 垂线 交线 l ⊥ α - 6 - 知识梳理 考点自测 直线与平面垂直的五个结论 (1) 若一条直线垂直于一个平面 , 则这条直线垂直于这个平面内的任意直线 . (2) 若两条平行线中的一条垂直于一个平面 , 则另一条也垂直于这个平面 . (3) 垂直于同一条直线的两个平面平行 . (4) 一条直线垂直于两平行平面中的一个 , 则这一条直线与另一个平面也垂直 . (5) 两个相交平面同时垂直于第三个平面 , 它们的交线也垂直于第三个平面 . - 7 - 知识梳理 考点自测 1 . 判断下列结论是否正确 , 正确的画 “ √ ”, 错误的画 “ × ” . (1) 已知直线 a , b , c , 若 a ⊥ b , b ⊥ c , 则 a ∥ c. ( 　　 ) (2) 直线 l 与平面 α 内的无数条直线都垂直 , 则 l ⊥ α . ( 　　 ) (3) 设 m , n 是两条不同的直线 , α 是一个平面 , 若 m ∥ n , m ⊥ α , 则 n ⊥ α . ( 　　 ) (4) 若两平面垂直 , 则其中一个平面内的任意一条直线垂直于另一个平面 . ( 　　 ) (5) 若平面 α 内的一条直线垂直于平面 β 内的无数条直线 , 则 α ⊥ β . ( 　　 ) × × √ × × - 8 - 知识梳理 考点自测 2 . 设 l , m , n 均为直线 , 其中 m , n 在平面 α 内 , 则 “ l ⊥ α ” 是 “ l ⊥ m 且 l ⊥ n ” 的 ( 　　 ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 A 解析 : 当 l ⊥ α 时 , l ⊥ m 且 l ⊥ n. 但当 l ⊥ m , l ⊥ n 时 , 若 m , n 不是相交直线 , 则得不到 l ⊥ α . 即 l ⊥ α 是 l ⊥ m 且 l ⊥ n 的充分不必要条件 . 故选 A . - 9 - 知识梳理 考点自测 3 . (2017 湖南岳阳一模 , 文 4) 已知 α , β 表示两个不同的平面 , m 为平面 α 内的一条直线 , 则 “ m ⊥ β ” 是 “ α ⊥ β ” 的 ( 　　 ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 A 解析 : 根据面面垂直的判定定理得 , 若 m ⊥ β , 则 α ⊥ β 成立 , 即充分性成立 , 若 α ⊥ β , 则 m ⊥ β 不一定成立 , 即必要性不成立 , 故 m ⊥ β 是 α ⊥ β 的充分不必要条件 , 故选 A . - 10 - 知识梳理 考点自测 4 . 如图所示 , 在立体图形 D-ABC 中 , 若 AB=CB , AD=CD , E 是 AC 的中点 , 则下列结论正确的是 ( 　　 ) A. 平面 ABC ⊥ 平面 ABD B. 平面 ABD ⊥ 平面 BDC C. 平面 ABC ⊥ 平面 BDE , 且平面 ADC ⊥ 平面 BDE D. 平面 ABC ⊥ 平面 ADC , 且平面 ADC ⊥ 平面 BDE C 解析 : ∵ AB=CB , 且 E 是 AC 的中点 , ∴ BE ⊥ AC , 同理有 DE ⊥ AC , 而 BE ∩ DE=E , ∴ AC ⊥ 平面 BDE. ∵ AC 在平面 ABC 内 , ∴ 平面 ABC ⊥ 平面 BDE. 又 AC 在平面 ADC 内 , ∴ 平面 ADC ⊥ 平面 BDE. 故选 C . - 11 - 知识梳理 考点自测 5 . (2017 湖北武昌 1 月调研 , 文 16) 在矩形 ABCD 中 , AB

查看更多