2020届二轮复习空间几何量学案(全国通用)
空间几何量
空间几何量主要有空间线段的长度、点面距离、异面直线的距离、异面直线所成的角、线面角及二面角等几何量.
· 空间线段的长度
空间线段 AB 的两个端点 A 、 B 之间的距离称为空间线段的长度.
· 点面距离
从平面 α 外一点 P 引平面的垂线,垂足设为 H,则点 P 和点 H 之间的距离称为 P 到平面 α 的距离.
· 异面直线的距离
设直线 a,b 是异面直线,则存在直线 l 与直线 a,b 均相交且垂直,此时直线 l 称为异面直线 a , b 的公垂线,直线 l 夹在直线 a,b 之间的部分称为异面直线 a , b 的公垂线段.异面直线 a,b 的公垂线段的长度称为异面直线 a , b 的距离.
· 异面直线所成的角
设直线 a,b 是异面直线,过空间一点 O 分别作直线 a,b 的平行线 aʹ,bʹ,我们把直线 aʹ,bʹ 所成的锐角或直角叫做异面直线 a,b 所成的角,或异面直线 a,b 的夹角.
· 线面角
一条直线 PA 和一个平面 α 相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点 A 叫做斜足.过斜线上斜足以外的一点向平面引垂线 PO,过垂足 O 和斜足 A 的直线 AO 叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.
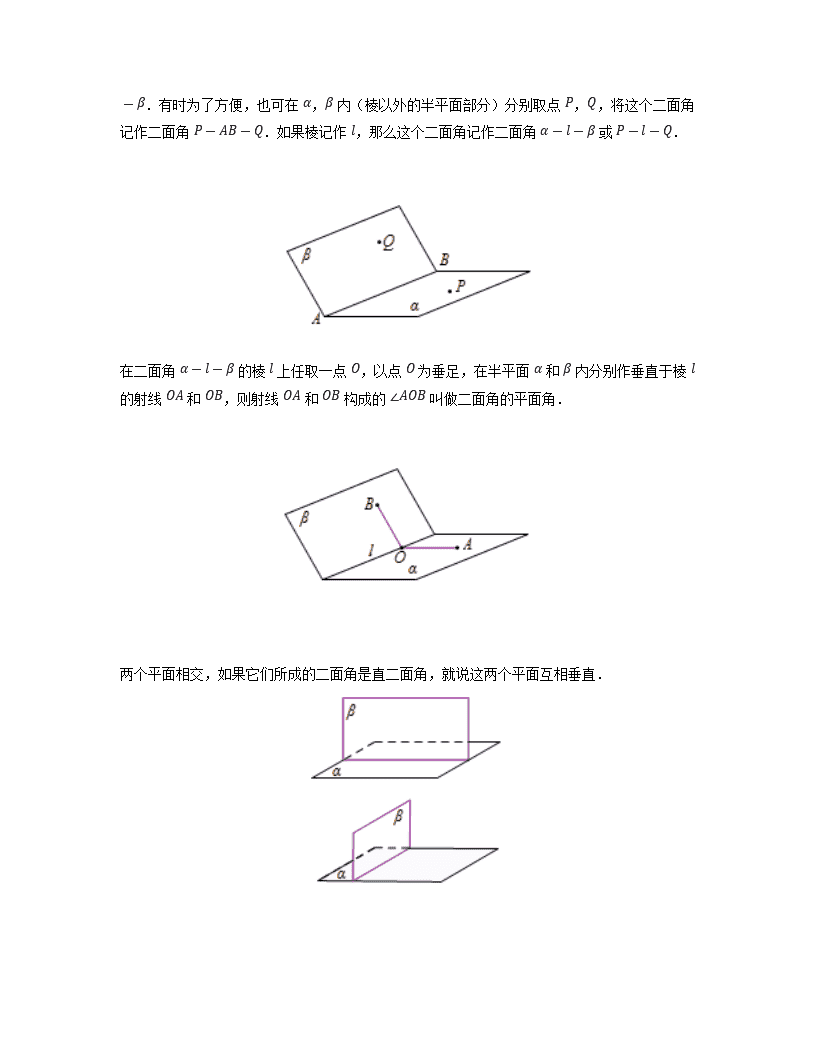
· 二面角
从一条直线出发的两个半平面所组成的图形叫做二面角(dihedral angle).这条直线叫做二面角的棱,这两个半平面叫做二面角的面.棱 AB 、面分别为 α,β 的二面角记作二面角 α-AB-β.
空间线段的长度
空间线段 AB 的两个端点 A 、 B 之间的距离称为空间线段的长度.
点面距离
从平面 α 外一点 P 引平面的垂线,垂足设为 H,则点 P 和点 H 之间的距离称为 P 到平面 α 的距离.
异面直线的距离
设直线 a,b 是异面直线,则存在直线 l 与直线 a,b 均相交且垂直,此时直线 l 称为异面直线 a , b 的公垂线,直线 l 夹在直线 a,b 之间的部分称为异面直线 a , b 的公垂线段.异面直线 a,b 的公垂线段的长度称为异面直线 a , b 的距离.
异面直线所成的角
设直线 a,b 是异面直线,过空间一点 O 分别作直线 a,b 的平行线 aʹ,bʹ,我们把直线 aʹ,bʹ 所成的锐角或直角叫做异面直线 a,b 所成的角,或异面直线 a,b 的夹角.
线面角
一条直线 PA 和一个平面 α 相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点 A 叫做斜足.过斜线上斜足以外的一点向平面引垂线 PO,过垂足 O 和斜足 A 的直线 AO 叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.一条直线垂直于平面,则称直线和平面所成的角是 90∘;一条直线和平面平行,或在平面内,则称直线和平面所成的角是 0∘.
二面角
从一条直线出发的两个半平面所组成的图形叫做二面角(dihedral angle).这条直线叫做二面角的棱,这两个半平面叫做二面角的面.棱 AB 、面分别为 α,β 的二面角记作二面角 α-AB-β
.有时为了方便,也可在 α,β 内(棱以外的半平面部分)分别取点 P,Q,将这个二面角记作二面角 P-AB-Q.如果棱记作 l,那么这个二面角记作二面角 α-l-β 或 P-l-Q.
在二面角 α-l-β 的棱 l 上任取一点 O,以点 O 为垂足,在半平面 α 和 β 内分别作垂直于棱 l 的射线 OA 和 OB,则射线 OA 和 OB 构成的 ∠AOB 叫做二面角的平面角.
两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.
精选例题
空间几何量
1. E,F,G,H 分别是空间四边形 ABCD 的各边中点.
(1)当空间四边形 ABCD 满足条件 时,四边形的形状是菱形.
(2)若 AC+BD=a,AC⋅BD=b,则 EF2+FG2= .
【答案】 AC=BD;a2-2b4
【分析】 由中位线定理可知 EF∥GH∥AC,EF=GH=12AC,
EH∥FG∥BD,EH=FG=12BD,
所以 EFGH 必为平行四边形.
因此(1)只要有邻边相等的条件.(2)中,由已知可得
EF2+FG2=14AC2+14BD2=14AC+BD2-2AC⋅BD=a2-2b4.
2. 如图所示,正方形 ABCD 所在平面与正方形 ABEF 所在平面成 60∘ 的二面角,则异面直线 AD 与 BF 所成的余弦值是 .
【答案】 24
3. 棱长为 1 的正方体 ABCD-A1B1C1D1 中,E 为 AA1 的中点,则平面 DEB1 与平面 ABCD 所成二面角 α 的余弦值为 .
【答案】 62
4. 若 P 是 △ABC 所在平面外一点,且 △PBC 和 △ABC 都是边长为 2 的正三角形,PA=6,那么二面角 P-BC-A 的大小为 .
【答案】 90∘
5. 如图,四边形 ABCD 和 ABMN 都是边长为 a 的正方形,所在两平面互相垂直,其中 E,F 分别在 AC,BN 上,且 AE=NF,则线段 EF 长的最小值为 .
【答案】 22a
【分析】 将四边形 ABCD 和 ABMN 铺平在一个平面内,连接 EF 交 AB 于点 O.
由 AE=NF,得 EF⊥AB,且 EF∥AD.
设 AE=NF=x,则 EO=2x2.
由 OFAN=BFBN,得 OFa=2a-x2a,解得 OF=2a-x2.
将四边形 ABCD 和 ABMN 折成直二面角后,则有 EO⊥平面ANMB,
所以 EF=EO2+OF2=x2-2ax+a2,
所以当 x=2a2 时,EF 长的最小值为 22a.
6. 如图,几何体 ABCDE 中,△ABC 是正三角形,EA 和 DC 都垂直于平面 ABC,且 EA=AB=2a,DC=a,F 为 EB 的中点,G 为 AB 的中点.
(1)求证:FD∥平面ABC;
【解】 因为 F 、 G 分别为 EB 、 AB 的中点,
所以 FG=12EA,FG∥AE.
又 EA 、 DC 都垂直于面 ABC,
所以 FG∥DC,且 FG=DC,
所以四边形 FGCD 为平行四边形,
所以 FD∥GC,
又 GC⊂ 面 ABC,FD⊄ 面 ABC.
所以 FD∥平面ABC.
(2)求二面角 B-FC-G 的正切值.
【解】 因为 △ABC 是正三角形,G 是 AB 的中点,
所以 BA⊥CG
又 FG∥EA,
且 EA⊥ 面 ABC,
所以 FG⊥BA,CG∩GF=G,
所以 BG⊥平面GFC.
作 GH⊥FC 于点 H,连 BH,
则 FC⊥ 面 GHB,
所以 FC⊥BH.
所以 ∠GHB 即为所求二面角的平面角.
因为 BG=GF=a,GC=3a,
所以 GH=32a,
所以 tan∠GHB=BGGH=a32a=233.
7. 已知正方形 ABCD,E,F 分别是边 AB,CD 的中点,将 △ADE 沿 DE 折起,如图所示.
(1)证明:BF∥平面ADE;
【解】 证明:E,F 分别是正方形 ABCD 的边 AB 、 CD 的中点.
所以 ED∥FD,且 EB=FD,
所以四边形 EBFD 是平行四边形,
所以 BF∥ED,
所以 ED⊂平面AED,而 BF⊄平面AED,
所以 BF∥平面AED.
(2)若 △ACD 为正三角形,求二面角 A-DE-C 的余弦值.
【解】 过点 A 作 AG⊥平面BCDE,垂足为 G,连接 GC,GD.
因为 △ACD 为正三角形,
所以 AC=AD,GC=GD,
所以 G 在 CD 的垂直平分线上.
又因为 EF 是 CD 的垂直平分线,
所以点 A 在平面 BCDE 内的射影 G 在直线 EF 上.
过 G 作 GH⊥ED,垂足为 H,连接 AH,则 AH⊥DE,
所以 ∠AHG 是二面角 A-DE-C 的平面角,即 ∠AHG=θ.
设原正方形 ABCD 的边长为 2a,连接 AF,
在折后图的 △AEF 中,AF=3a,EF=2AE=2a,
所以 △AEF 为直角三角形,AG⋅EF=AE⋅AF,所以 AG=32a.
在 Rt△ADE 中,AH⋅DE=AD⋅AE,所以 AH=2a5,GH=a25.
所以 cosθ=GHAH=14.
8. 如图,在三棱锥 P-ABC 中,PA⊥ 底面 ABC,D 是 PC 的中点.已知 ∠BAC=π2,AB=2,AC=23,PA=2.求:
(1)三棱锥 P-ABC 的体积;
【解】
S△ABC=12AB⋅AC=12×2×23=23,
三棱锥 P-ABC 的体积为
V=13S△ABC×PA=13×23×2=433.
(2)异面直线 BC 与 AD 所成的角的大小(结果用反三角函数值表示).
【解】 如图,
取 PB 的中点 E,连接 DE,AE,则 ED∥BC,
所以 ∠ADE(或其补角)是异面直线 BC 与 AD 所成的角.
在 △ADE 中,DE=2,AE=2,AD=2,所以
cos∠ADE=22+22-22×2×2=34,
所以
∠ADE=arccos34.
因此,异面直线 BC 与 AD 所成的角的大小是 arccos34.
9. 已知三棱锥 P-ABC 中, PA⊥平面 ABC,AB⊥AC ,PA=AC=12AB,N 为 AB 上一点,AB=4AN ,M,S 分别为 PB,BC 的中点.
(1)证明: CM⊥SN ;
【解】 设 PA=1 ,以 A 为原点,射线 AB,AC,AP 分别为 x,y,z 轴正向建立空间直角坐标系如图.
则
P0,0,1,C0,1,0,B2,0,0,M1,0,12,N12,0,0,S1,12,0.
所以
CM=1,-1,12,SN=-12,-12,0,
因为 CM⋅SN=-12+12+0=0 ,所以 CM⊥SN .
(2)求 SN 与平面 CMN 所成角的大小.
【解】 NC=-12,1,0 ,
设 a=x,y,z 为平面 CMN 的一个法向量,
则
x-y+12z=0,-12x+y=0.
令 x=2 ,得 a=2,1,-2 .
因为
cosa,SN=-1-123×22=22,
所以 SN 与平面 CMN 所成角为 45∘ .
10. 如图,三角形 ABC 是边长为 4 正三角形,PA⊥底面ABC,PA=7,点 D 是 BC 的中点,点 E 在 AC 上,且 DE⊥AC.
(1)证明:DE⊥平面PAC;
【解】 因为 PA⊥底面ABC,DE⊂底面ABC,
所以 PA⊥DE.
又 DE⊥AC,PA∩AC=A,
所以 DE⊥平面PAC.
(2)求直线 AD 和平面 PDE 所成角的正弦值.
【解】 方法一:
由(1)知,DE⊥平面PAC,又 DE⊂平面PDE,
所以 平面PDE⊥平面PAC.
过点 A 作 AF⊥PE,连接 DF.
因为 平面PDE⊥平面PAC,平面PDE∩平面PAC=PE,AF⊂平面PAC,
所以 AF⊥平面PDE.
所以 ∠ADF 为直线 AD 和平面 PDE 所成角的平面角.
因为 △ABC 是边长为 4 正三角形,
所以 AD=23,AE=4-CE=4-12CD=3.
又因为 PA=7,
所以 PE=PA2+AE2=72+32=4,AF=AE⋅PAPE=374.
所以 sin∠ADF=AFAD=218.
即直线 AD 和平面 PDE 所成角的正弦值为 218.
方法二:
如图所示,以点 A 为坐标原点,AD 所在直线为 x 轴建立如图空间直角坐标系.
因为在正 △ABC 中,DE⊥AC,
所以 AD=23,AE=3.
所以 A0,0,0,P0,0,7,D23,0,0,E332,32,0.
易知 PD=23,0,-7,PE=332,32,-7,
AD=23,0,0.
设 n=x,y,z是平面PDE 的一个法向量,则 n⋅PD=23x-7z=0,n⋅PE=332x+32y-7z=0.
解得 x=216z,y=76z.
故可取 n=21,7,6.
于是 cos⟨n,AD⟩=n⋅ADn⋅AD=678×23=218.
空间线段的长度
1. 三个平面两两垂直,它们的交线交于一点 O,且点 P 到三个平面的距离分别为 3,4,5,则 OP 的长为 .
【答案】 52
2. 如图,在棱长为 2 的正方体 ABCD-A1B1C1D1 中,E 为 BC 的中点,点 P 在底面 ABCD 上移动,且满足 B1P⊥D1E,则线段 B1P 的长度的最大值为 .
【答案】 3
3. 如图所示,ABCD-A1B1C1D1 是棱长为 a 的正方体,M,N 分别是下底面的棱 A1B1,B1C1 的中点,P 是上底面的棱 AD 上的一点,AP=a3,过 P,M,N 的平面交上底面于 PQ,Q 在 CD 上,则 PQ= .
【答案】 22a3
4. 已知直二面角 α-l-β,点 A∈α,AC⊥l,C 为垂足,B∈β,BD⊥l,D 为垂足,若 AB=2,AC=BD=1,则 CD 的长为 .
【答案】 2
【分析】 如图,连接 BC,
因为二面角 α-l-β 为直二面角,AC⊂α,且 AC⊥l,
所以 AC⊥β.
又 BC⊂β,
所以 AC⊥BC,
所以 BC2=AB2-AC2=3,
又 BD⊥CD,
所以 CD=BC2-BD2=2.
5. 如图所示,A 是 △BCD 所在平面外一点,M,N 分别是 △ABC 和 △ACD 的重心,若 BD=6,则 MN= .
【答案】 2
【分析】 设 AM,AN 与 BC,CD 分别交于 E,F 两点,由于 M,N 为重心,则 E,F 分别为中点,且 MNEF=AMAE=ANAF=23,又 EF=12BD=3,所以 MN=2.
6. 如图,在棱长为 a 的正方体 ABCD-A1B1C1D1 中,E,F,P,Q 分别是 BC,C1D1,AD1,BD 的中点.
(1)求证:PQ∥平面DCC1D1;
【解】 连接 AC,CD1,
因为 P,Q 分别为 AD1,AC 中点,
所以 PQ∥CD1.
又 CD1⊂平面DCC1D1,PQ⊄平面DCC1D1,
所以 PQ∥平面DCC1D1.
(2)求 PQ 的长;
【解】 由(1)易知 PQ=12D1C=22a.
(3)求证:EF∥平面BB1D1D.
【解】 取 B1C1 的中点 E1,连接 EE1,FE1,
则有 FE1∥B1D1,EE1∥BB1.
所以 平面EE1F∥平面BB1D1D.
又 EF⊂平面EE1F,
所以 EF∥平面BB1D1D.
7. 平行六面体 ABCD-A1B1C1D1 的棱长都为 2,∠A1AB=∠A1AD=∠BAD=60∘,E 是 DC 的中点,F 是 B1C 的中点.
(1)求证:向量 BD,BB1,EF 共面;
【解】 设 AB=a,AD=b,AA1=c,
则 BB1=c,BD=b-a,
EF=AF-AE=AB+12BC1-AD+12DC=a+12b+c-b+12a=12a-b+c=12BB1-12BD.
由共面向量定理知,向量 BD,BB1,EF 共面.
(2)求 ∣D1F∣.
【解】 由题意知 ∣a∣=∣b∣=∣c∣=2,
而且 ⟨a,b⟩=⟨b,c⟩=⟨a,c⟩=60∘.
D1F=AF-AD1=a+12b+c-b+c=a-12b-12c,
∣D1F∣2=a-12b-12c⋅a-12b-12c=a2+14b2+14c2-a⋅b-a⋅c+12b⋅c=3.
所以 ∣D1F∣=3.
8. 如图,在正三棱柱 ABC-A1B1C1 中,AB=3,AA1=4,M 为 AA1 的中点,P 是 BC 上一点,且由点 P 沿棱柱侧面经过棱 CC1 到点 M 的最短路线长为 29,设这条最短路线与 CC1 的交点为 N,求:
(1)该三棱柱的侧面展开图的对角线长;
【解】 正三棱柱 ABC-A1B1C1 的侧面展开图是一个长为 9,宽为 4 的矩形,其对角线长为 92+42=97.
(2)PC 和 NC 的长.
【解】 如图,将侧面 BB1C1C 绕棱 CC1 旋转 120∘ 使其与侧面 AA1C1C 在同一平面上,点 P 运动到点 P1 的位置,连接 MP1,
则 MP1 就是由点 P 沿棱柱侧面经过棱 CC1 到点 M 的最短路线.
设 PC=x,则 P1C=x.
在 Rt△MAP1 中,AM2+AP12=MP12,
即 22+x+32=29,解得 x=2(x=-8 舍去).
所以 PC=P1C=2,
因为 NCMA=P1CP1A=25,
所以 NC=45.
9. 等边三角形 ABC 的边长为 a,沿平行于 BC 的线段 PQ 折起,使平面 APQ⊥平面PBCQ,设点 A 到直线 PQ 的距离为 x,AB 的长为 d.试探求:x 为何值时,d2 取得最小值?最小值是多少?
【解】 图(1)为折叠前对照图,图(2)为折叠后空间图形.
因为折叠后,平面APQ⊥平面PBCQ,且 AR⊥PQ,
所以 AR⊥平面PBCQ.
所以 AR⊥RB.
在 Rt△BRD 中,BR2=BD2+RD2=12a2+32a-x2.
又 AR2=x2,故 d2=BR2+AR2=2x2-3ax+a2=2x-34a2+58a20
1,设点 A 到直线 A1C 的距离和到平面 DCB1A1 的距离分别为 d1,d2,则 d1d2 的取值范围是 .
【答案】 233,2
5. 已知 △ABC 是边长为 2 的正三角形,点 P 是平面 ABC 外一点,且 PA=PB=3,PC=7,则点 P 到平面 ABC 的距离是 .
【答案】 2153
6. 如图,P 为矩形 ABCD 所在平面外一点,且 PA⊥平面ABCD,Q 为线段 AP 的中点,若 AB=AP=2,BC=4,求点 P 到平面 BQD 的距离.
【解】 因为 Q 为线段 PA 的中点,
所以 P 点到平面 QBD 的距离等于 A 点到平面 QBD 的距离.
如图,在平面 ABCD 内过 A 作 BD 的垂线 AE,交 BD 于 E,连接 QE.
因为 PA⊥平面ABCD,所以 BD⊥PA,
又 PA∩AE=A,
所以 BD⊥平面QAE.
在平面 QAE 内过 A 作 AH⊥QE 于 H.
所以 BD⊥AH.
又 QE∩BD=E,所以 AH⊥平面BQD.
所以 A 点到平面 BQD 的距离为 AH 的长.
在 Rt△ABD 中,AD=4,AB=2,所以 BD=25.
所以 AE=455.
在 Rt△QAE 中,QE=AQ2+AE2=215.
所以 AH=AQ⋅AEQE=1×455215=42121,
即点 P 到平面 BQD 的距离为 42121.
7. 如图,在直三棱柱 ABC-A1B1C1 中,AB1⊥BC1,AB=CC1=2.
(1)求证:平面A1BC1⊥平面ABB1A1.
【解】 由已知得侧面 ABB1A1 是菱形,
所以 AB1⊥A1B,又知 AB1⊥BC1,
因此 AB1上平面A1BC1,
所以 AB1⊥A1C1,
因为 ABC-A1B1C1 是直三棱柱,
所以 AA1⊥底面A1B1C1,
从而 A1C1⊥平面ABB1A1,
又 A1C1⊂平面A1BC1,
所以 平面A1BC1⊥平面ABB1A1.
(2)求点 C 到平面 A1BC1 的距离.
【解】 连接 B1C,交 BC1 于 O,
则 O 是 B1C 的中点,
所以点 C 到平面 A1BC1 的距离等于 B1 到平面 A1BC1 的距离,
设 AB1∩A1B=P,
则由(1)知 B1P⊥平面A1BC1,
即 B1P 为 B1 到平面 A1BC1 的距离,
由条件可得 B1P=2,
所以点 C 到平面 A1BC1 的距离等于 2.
8. 如图,在四棱锥 P-ABCD 中,ABCD 是正方形,PD⊥ 平面 ABCD,PD=AB=2,E,F,G 分别是 PC,PD,BC 的中点.
(1)求证:平面 PAB∥ 平面 EFG;
【解】 E,G 分别是 PC,BC 的中点得 EG∥PB,
因为 EG⊄ 平面 PAB,PB∥ 平面 PAB
所以 EG∥ 平面 PAB
又 E,F 分别是 PC,PD 的中点,
所以 EF∥CD,又 AB∥CD
所以 EF∥AB
因为 EF⊈ 平面 PAB,AB⊆ 平面 PAB
所以 EF∥ 平面 PAB,
又因为 EG,EF⊂ 平面 EFG,EG∩EF=E,
所以平面 PAB∥ 平面 EFG.
(2)在线段 PB 上确定一点 Q,使 PC⊥ 平面 ADQ,并给出证明;
【解】 Q 为 PB 的中点,连 QE,DE,又 E 是 PC 的中点,
所以 QE∥BC,又 BC∥AD,所以 QE∥AD
所以平面 ADQ,即平面 ADEQ,
因为 PD⊥ 平面 ABCD,CD⊂ 平面 ABCD
所以 PD⊥DC,又 PD=AB=2,ABCD 是正方形,
所以等腰直角三角形 PDC
由 E 为 PC 的中点知 DE⊥PC.
因为 PD⊥ 平面 ABCD,AD⊂ 平面 ABCD
所以 PD⊥AD,
又 AD⊥DC,PD∩CD=D,
所以 AD⊥ 面 PDC.
因为 PC⊂ 面 PDC
所以 AD⊥PC,且 AD∩DE=D.
所以 PC⊥ 平面 ADEQ,
即 PC⊥ 平面 ADQ
由于 EQ∥BC∥AD,
所以 ADEQ 为平面四边形,
由 PD⊥ 平面 ABCD,得 AD⊥PD,
又 AD⊥CD,PD∩CD=D,
所以 AD⊥ 平面 PDC,
因为 PC⊂ 平面 PDC,
所以 AD⊥PC,
又三角形 PDC 为等腰直角三角形,E 为斜边中点,
所以 DE⊥PC,AD∩DE=D,
所以 PC⊥ 平面 ADQ.
(3)证明平面 EFG⊥ 平面 PAD,并求点 D 到平面 EFG 的距离.
【解】 因为 CD⊥AD,CD⊥PD,AD∩PD=D,
所以 CD⊥ 平面 PAD,
又 EF∥CD,
所以 EF⊥ 平面 PAD,
因为 EF⊂ 平面 EFG,
所以平面 EFG⊥ 平面 PAD.
取 AD 中点 H,连接 FH,GH,
则 HG∥CD∥EF,平面 EFGH 即为平面 EFG,
在平面 PAD 内,作 DO⊥FH,垂足为 O,
则 DO⊥ 平面 EFGH,
DO 即为 D 到平面 EFG 的距离,
在三角形 PAD 中,H,F 为 AD,PD 中点,
所以 DO=FDsin45∘=22.
即 D 到平面 EFG 的距离为 22.
9. 如图,正四棱柱 ABCD-A1B1C1D1 中,底面边长为 22,侧棱长为 4.E,F 分别为棱 AB,BC 的中点,EF∩BD=G.
(1)求证:平面 B1EF⊥ 平面 BDD1B1;
【解】 如图连接 AC.
∵正四棱柱 ABCD-A1B1C1D1 的底面是正方形,
∴ AC⊥BD,又 AC⊥D1D,故 AC⊥ 平面 BDD1B1.
∵ E,F 分别为 AB,BC 的中点,故 EF∥AC,
∴ EF⊥ 平面 BDD1B1.又 EF⊂平面B1EF,
∴平面 B1EF⊥ 平面 BDD1B1.
证法二:
∵ BE=BF,∠EBD=∠FBD=45∘,∴ EF⊥BD.又 EF⊥D1D,
∴ EF⊥ 平面 BDD1B1.又 EF⊂平面B1EF,∴平面 B1EF⊥ 平面 BDD1B1.
(2)求点 D1 到平面 B1EF 的距离 d;
【解】 如图,在对角面 BDD1B1 中,作 D1H⊥B1G,垂足为 H.
∵ 平面 B1EF⊥ 平面 BDD1B1,且平面 B1EF∩ 平面 BDD1B1=B1G,
∴ D1H⊥ 平面 B1EF,且垂足为 H,
∴ 点 D1 到平面 B1EF 的距离 d=D1H.
∵ △D1HB1∽△B1BG,
∴ D1HB1B=D1B1B1G,
∴ d=D1H=B1B2B1G=4242+12=161717.
(3)求三棱锥 B1-EFD1 的体积 V.
【解】 根据题意可得体积为
V=VB1-EFD1=VD1-B1EF=13⋅d⋅S△B1EF=13⋅1617⋅12⋅2⋅17=163.
10. 如图,在四棱锥 P-ABCD 中, PD⊥平面 ABCD , PD=DC=BC=1 , AB=2 , AB∥DC , ∠BCD=90∘ .
(1)求证: PC⊥BC ;
【解】 法一:
因为 PD⊥平面 ABCD , BC⊂平面 ABCD ,所以 PD⊥BC .
因为 ∠BCD=90∘ ,所以 CD⊥BC .
又 PD∩CD=D ,所以 BC⊥平面 PCD .
而 PC⊂平面 PCD , 所以 PC⊥BC .
法二:
过点 D 作 DE∥BC 交 AB 于 E ,则 E 为 AB 中点.
因为 PD⊥平面 ABCD ,所以 PD⊥CD , PD⊥DE .
因为 ∠BCD=90∘ ,所以 CD⊥BC ,所以 CD⊥DE .
以 D 为坐标原点 O , DE 为 x 轴, DC 为 y 轴, DP 为 z 轴,建立空间直角坐标系,如图,
则
OD0,0,0,A1,-1,0,B1,1,0,C0,1,0,P0,0,1.
所以
PC=0,1,-1,BC=-1,0,0,PC⋅BC=0,
所以 PC⊥BC .
(2)求点 A 到平面 PBC 的距离.
【解】 法一:
如图,过点 A 作 BC 的平行线交 CD 的延长线于 E ,过点 E 作 PC 的垂线,垂足为 F ,
则有 AE∥平面 PBC ,所以点 A 到平面 PBC 的距离等于点 E 到平面 PBC 的距离.
又 EF⊥PC , BC⊥平面 PCD ,则 EF⊥BC .
而 BC∩PC=C ,所以 EF⊥平面 PBC . EF 即为 E 到平面 PBC 的距离.
又因为 AE∥BC , AB∥CD ,所以四边形 ABCE 为平行四边形.
所以 CE=AB=2 .
又PD=CD=1 , PD⊥平面 ABCD , CD⊂平面 ABCD ,
所以 PD⊥CD , ∠PCD=45∘ .
所以 EF=2 ,即点 A 到平面 PBC 的距离为 2 .
法二:
设平面 PBC 的一个法向量为 n=x,y,z ,点 A 到平面 PBC 的距离为 d ,则由
n⊥PC,n⊥BC,
得
y-z=0,-x=0,
解得
x=0,y=z.
令 z=1 ,则 y=1 ,得
n=0,1,1.
又
PA=1,-1,-1,
故
d=PA⋅nn=22=2.
所以点 A 到平面 PBC 的距离为 2 .
异面直线的距离
1. 正方体 ABCD-A1B1C1D1 的棱长为 a,那么
(1)直线 BA1 与 CC1 所成角的大小为 .
(2)直线 BA1 与 B1C 所成角的大小为 .
(3)异面直线 BC 与 AA1 的距离为 .
(4)异面直线 BA1 与 CC1 的距离为 .
【答案】 45∘;60∘;a;a
2. 在棱长为 1 的正方体 ABCD-A1B1C1D1 中,E 为 A1B1 的中点,则异面直线 D1E 和 BC1 间的距离是 .
【答案】 63
【分析】 如图:连接 AD1 、 AE 、 AC1 、 EC1.
易得 BC1∥ 面 AED1.
故异面直线 D1E 和 BC1 间的距离即为线 BC1 与面 AED1 的距离.
在四面体 AED1C1 中,根据等体积易得 C1 到面 AED1 的距离为 63.
即 所求距离为 63.
3. 在 60∘ 的二面角 α-l-β 的面 α 内一点 A 到面 β 的距离为 3,A 在 β 上的射影为 Aʹ,则 Aʹ 到面 α 的距离为 ;异面直线 AAʹ 与 l 间的距离为 .
【答案】 32;1
4. 如图,正四棱锥 S-ABCD 的高 SO=2,底面边长 AB=2,求异面直线 BD 与 SC 之间的距离为 .
【答案】 255
【解】 连接 OC,做 OE⊥SC 于点 E,则 BD⊥OC,BD⊥SO,∴BD⊥平面SOC,∴BD⊥OE,∴OE 就是异面直线 BD 与 SC 的公垂线段,SO=2,OC=1,计算得 SC=5,OE=255.
5. 已知正方体 ABCD-A1B1C1D1 的棱长是 1 ,则直线 DA1 与 AC 间的距离为 .
【答案】 33
【分析】
以 A 为原点, AB 为 x 轴正方向建立空间直角坐标系, M , N 分别是 A1D , AC 上的点,且 MN 是 DA1 与 AC 间的垂线段.
可设 M(0,m,1-m) , N(t,t,0) ,利用 MN⊥A1D 且 MN⊥AC 可求得 M , N 坐标,从而求出 DA1 与 AC 间的距离.
6. 如图,正方体 ABCD-A1B1C1D1 的棱长为 a,M、N 分别是棱 AA1 、 CC1 上的动点,且 AM=C1N.
(1)求证:四边形 MBND1 是平行四边形;
【解】 在 D1D 上取一点 E,使 D1E=A1M,
则四边形 A1MED1 为平行四边形,
则 ME∥A1D1,ME=A1D1.
又 A1D1∥BC,A1D1=BC,
所以 ME∥BC,ME=BC
于是四边形 MBCE 为平行四边形,
因此 MB∥EC,MB=EC.
由已知得 D1E∥NC,D1E=NC,
所以四边形 D1ECN 为平行四边形.
于是 EC∥D1N,EC=D1N.
所以 MB∥D1N,MB=D1N,
故四边形 MBND1 是平行四边形.
(2)求四边形 MBND1 面积的最小值.
【解】 S平行四边形MBND1=2S△MBD1,
在 △MBD1 中,BD1=3a.
要求 △MBD1 面积的最小值,需求 M 到 BD1 的最小距离,亦即求异面直线 AA1 与 BD1 的距离.
当 M 为 A1A 的中点时,N 也为 C1C 的中点,
设 MN∩D1B=O,此时 平行四边形 MBND1 为菱形,
所以 MN⊥D1B.
又四边形 A1MNC1 为平行四边形,
MN∥A1C1,
又 A1A⊥A1C1,
所以 A1A⊥MN,
于是 MO 为异面直线 A1A 与 D1B 的公垂线段,且
MO=12MN=12A1C1=2a2,
所以
S△MBD1min=12D1B⋅MO=12⋅3a⋅22a=64a2,
从而
S平行四边形MBND1min=62a2,
故四边形 MBND1 面积的最小值为 62a2.
7. 如图,在直三棱柱 ABC-A1B1C1 中,∠ABC=90∘,AB=1,BC=32,AA1=2,点 D 在棱 BB1 上,BD=13BB1;B1E⊥A1D,垂足为 E,求:
(1)异面直线 A1D 与 B1C1 的距离;
【解】 解法一:
由直三棱柱的定义知 B1C1⊥B1D,又因为 ∠ABC=90∘,因此 B1C1⊥A1B1,
从而 B1C1⊥ 平面 A1B1D,得 B1C1⊥B1E.
又 B1E⊥A1D,故 B1E 是异面直线 B1C1 与 A1D 的公垂线.
由 BD=13BB1 知 B1D=43,在 Rt△A1B1D 中,
A1D=A1B12+B1D2=1+432=53.
又因
S△A1B1D=12A1B1⋅B1D=12A1D⋅B1E.
故
B1E=A1B1⋅B1DA1D=1⋅4353=45.
解法二:
如图,以 B 点为坐标原点 O 建立空间直角坐标系 O-xyz,
则 A0,1,0,A10,1,2,B0,0,0,B10,0,2,C132,0,2,D0,0,23,因此
AA1=0,0,2,AB=0,-1,0,B1C1=32,0,0,A1D=0,-1,-43.
设 E0,y0,z0,则
B1E=0,y0,z0-2,
因此
B1E⋅B1C1=0,
从而 B1C1⊥B1E.
又由题设 B1E⊥A1D,故 B1E 是异面直线 B1C1 与 A1D 的公垂线.
下面求点 E 的坐标.
因 B1E⊥A1D,即 B1E⋅A1D=0,从而
y0+43z0-2=0, ⋯⋯①
又
A1E=0,y0-1,z0-2,
且 A1E∥A1D,得
y0-11=z0-243, ⋯⋯②
联立 ①,②,解得
y0=1625,z0=3825,
即 E0,1625,3825,
B1E=0,1625,-1225.
所以
B1E=16252+-12252=45.
(2)四棱锥 C-ABDE 的体积.
【解】 解法一:
由(1)知 B1C1⊥ 平面 A1B1D,
又 BC∥B1C1,故 BC⊥ 平面 ABDE,即 BC 为四棱锥 C-ABDE 的高.
从而所求四棱锥的体积为
V=VC-ABDE=13×S×BC,
其中 S 为四边形 ABDE 的面积.
如图,过 E 作 EF⊥BD,垂足为 F.
在 Rt△B1ED 中,
ED=B1D2-B1E2=432-452=1615,
又因为
S△B1ED=12B1E⋅DE=12B1D⋅EF,
故
EF=B1E⋅DEB1D=1625.
因 △A1AE 的边 A1A 上的高
h=A1B1-EF=1-1625=925,
故
S△A1AE=12A1A⋅h=12⋅2⋅925=925.
又因为
S△A1B1D=12A1B1⋅B1D=12⋅1⋅43=23,
从而
S=S四边形A1ABB1-S△A1AE-S△A1B1D=2-925-23=7375.
所以
V=13⋅S⋅BC=13⋅7375⋅32=73150.
解法二:
由 BC⊥AB,BC⊥DB,故 BC⊥ 面 ABDE.即 BC 为四棱锥 C-ABDE 的高.
下面求四边形 ABDE 的面积.
因为 S四边形ABDE=S△ABE+S△BDE,AB=1,BD=23,而
S△ABE=12ABz0=12⋅1⋅3825=1925,S△BDE=12BDy0=12⋅23⋅1625=1675.
故 S四边形ABDE=1925+1675=7375.所以
VC-ABDE=13⋅S四边形ABDE⋅BC=13⋅7375⋅32=73150.
8. 如图,在 △ABC 中,B=90∘,AC=152,D,E 两点分别在 AB,AC 上,使 ADDB=AEEC=2,DE=3.现将 △ABC 沿 DE 折成直二面角,求:
(1)异面直线 AD 与 BC 的距离;
【解】 如图1中,
因为 ADDB=AECE,所以 BE∥BC.
又因为 B=90∘,从而 AD⊥DE.
在图2中,
因 A-DE-B 是直二面角,AD⊥DE,
故 AD⊥ 底面 DBCE,从而 AD⊥DB.
而 DB⊥BC,故 DB 为异面直线 AD 与 BC 的公垂线.
下面求 DB 之长.在图 1 中,由
ADDB=AEEC=2,
得
DEBC=ADAB=23.
又已知 DE=3,从而
BC=32DE=92,AB=AC2-BC2=1522-922=6.
因 DBAB=13,故
DB=2.
即异面直线 AD 与 BC 的距离为 2.
(2)二面角 A-EC-B 的大小(用反三角函数表示).
【解】 方法一:在图2中,过 D 作 DF⊥CE,交 CE 的延长线于 F,连接 AF.
由(1)知,AD⊥ 底面 DBCE,由三垂线定理知 AF⊥FC,
故 ∠AFD 为二面角 A-EC-B 的平面角.
在底面 DBCE 中,∠DEF=∠BCE,所以
DB=2,EC=13⋅152=52,
因此
sin∠BCE=DBEC=45.
从而在 Rt△DFE 中,
DE=3,DF=DEsin∠DEF=DEsin∠BCE=125.
在 Rt△AFD,中
AD=4,tan∠AFD=ADDF=53.
因此所求二面角 A-EC-B 的大小为 arctan53.
方法二:如图3,
由(1)知,以 D 点为坐标原点,DB,DE,DA 的方向为 x,y,z 轴的正方向建立空间直角坐标系,则
D0,0,0,A0,0,4,C2,92,0,E0,3,0.
所以
CE=-2,-32,0,AD=0,0,-4,
过 D 作 DF⊥CE,交 CE 的延长线于 F,连接 AF.
设 Fx0,y0,0,从而
DF=x0,y0,0,EF=x0,y0-3,0,
由 DF⊥CE,有
DF⋅CE=0,
即
2x0+32y0=0, ⋯⋯①
又由 CE∥EF,得
x02=y0-332, ⋯⋯②
联立①、②,解得
x0=-3625,y0=4825,
即
F-3625,4825,0,
得
AF=-3625,4825,-4,
因为
AF⋅CE=-3625⋅-2+4825⋅-32=0,
故 AF⊥CE,又因 DF⊥CE,
所以 ∠DFA 为所求的二面角 A-EC-B 的平面角.
因 DF=-3625,4825,0,有
DF=-36252+48252=125,AD=4,
所以
tan∠AFD=ADDF=53.
因此所求二面角 A-EC-B 的大小为 arctan53.
9. 如图,在直三棱柱 ABC-A1B1C1 中,AB=4,AC=BC=3,D 为 AB 的中点.
(1)求异面直线 CC1 和 AB 的距离;
【解】 因为 AC=BC,D 为 AB 的中点,故 CD⊥AB.
又在直三棱柱中,CC1⊥ 平面 ABC,故 CC1⊥CD,
所以异面直线 CC1 和 AB 的距离为 CD=BC2-BD2=5.
(2)若 AB1⊥A1C,求二面角 A1-CD-B1 的平面角的余弦值.
【解】 由 CD⊥AB,CD⊥BB1,AB∩BB1=B,
故 CD⊥ 平面 A1ABB1,
从而 CD⊥DA1,CD⊥DB1,
故 ∠A1DB1 为所求的二面角 A1-CD-B1 的平面角.
因为 A1D 是 A1C 在平面 A1ABB1 上的射影,
又已知 AB1⊥A1C,由三垂线定理的逆定理得 AB1⊥A1D,
从而 ∠A1AB1,∠A1DA 都与 ∠B1AB 互余,
因此
∠A1AB1=∠A1DA,
所以 Rt△A1AD∽Rt△B1A1A.因此
AA1AD=A1B1AA1,
得
AA12=AD⋅A1B1=8,
从而
A1D=AA12+AD2=23,B1D=A1D=23,
所以在 △A1DB1 中,由余弦定理得
cos∠A1DB1=A1D2+B1D2-A1B122⋅A1D⋅B1D=13.
10. 如图,在四棱锥 P-ABCD 中.PD⊥ 平面 ABCD,PA 与平面 ABD 所成的角为 60∘,在四边形 ABCD 中,∠D=∠DAB=90∘,AB=4,CD=1,AD=2.
(1)建立适当的坐标系,并写点 B,P 的坐标;
【解】 建立如图所示的空间直角坐标系,
因为 ∠D=∠DAB=90∘,AB=4,CD=1,AD=2,
所以 A2,0,0,C0,1,0,B2,4,0.
由 PD⊥ 平面 ABCD.得 ∠PAD 为 PA 与平面 ABCD 所成的角,所以 ∠PAD=60∘.
在 Rt △PAD 中,由 AD=2,得 PD=23,所以 P0,0,23.
(2)求异面直线 PA 与 BC 所成的角的余弦值;
【解】 因为 PA=2,0,-23,BC=-2,-3,0.
所以 cosPA,BC=2×-2+0×-3+-23×0413=-1313,
所以 PA 与 BC 成成的角的余弦值为 1313.
(3)求异面直线 PA 与 BC 之间的距离;
【解】 由(2)知 PA=2,0,-23,BC=-2,-3,0.
设向量 n=x,y,z,且 n⋅PA=2x-23z=0,n⋅BC=-2x-3y=0,取 x=3 得 n=3,-2,3.
分别取 PA 上点 A 和 BC 上点 B,则 AB=0,4,0.
所以 d=AB⋅nn=0,4,0⋅3,-2,332+-22+32=2,即异面直线 PA 与 BC 的距离为 2.
(4)若 PB 的中点为 M,求平面 AMC 与平面 PBC 所成的角的大小.
【解】 因为 M 为 PB 的中点,所以点 M 的坐标为 1,2,3,
所以 AM=-1,2,3,所以 CM=1,1,3,PB=2,4,-23.
因为 AM⋅PB=-1×2+2×4+3×-23=0,CM⋅PB=1×2+1×4+3×-23=0,
所以 AM⊥PB,CM⊥PB.
所以 PB⊥ 平面 AMC.
而 PB⊂ 平面 PBC,所以平面 AMC⊥ 平面 PBC.
即平面 AMC 与平面 PBC 所成角的大小为 90∘.
异面直线所成的角
1. 直棱柱 ABC-A1B1C1 中,∠BCA=90∘,M,N 分别是 A1B1,A1C1 的中点,BC=CA=CC1,则 BM 与 AN 所成的角的余弦值为 .
【答案】 3010
【分析】 直三棱柱 ABC-A1B1C1 中,∠BCA=90∘,M,N 分别是 A1B1,A1C1 的中点.
如上图所示,取 BC 的中点为 O,连接 ON 、 AO,
因为 M,N 分别是 A1B1,A1C1 的中点,所以 MN∥B1C1 且 MN=12B1C1.
又因为 OB∥B1C1 且 OB=12B1C1,所以 MN∥OB 且 MN=OB,所以 MNOB 是平行四边形,所以 BM 与 AN 所成角就是 ∠ANO.
不妨设 BC=CA=CC1=2,则 CO=1,AO=5,AN=5,MB=2+4=6.
在 △ANO 中,由余弦定理得:cos∠ANO=AN2+NO2-AO22AN⋅NO=625×6=3010.
2. 在正三棱柱 ABC-A1B1C1 中,若 AB=2BB1,则 AB1 与 C1B 所成角的大小为 .
【答案】 90∘
3. 如图,在棱长都相等的四面体 SABC 中,给出如下三个命题:
① 异面直线 AB 与 SC 所成的角为 60∘;
② BC 与平面 SAB 所成角的余弦值为 33;
③ 二面角 S-BC-A 的余弦值为 13,其中所有正确命题的序号为 .
【答案】 ②③
4. 如图,PA⊥平面 ABC,∠ACB=90∘,且 PA=AC=BC=a,则异面直线 PB 与 AC 所成角的的正切值等于 .
【答案】 2
【解】 如图所示:
过 B 作 BD∥AC 且 BD=AC,则四边形 ADBC 为矩形,
从而 BD∥AC,∴ ∠PBD 是异面直线 PB 与 AC 所成角的平面角.
∵ PA⊥平面 ABC,BD⊥AD,
∴ BD⊥PD.
又∵ PA=AD=a,
∴ PD=2a,
∴ tan∠PBD=PDBD=2.
5. 如图,在四面体 ABCD 中,截面 PQMN 是正方形,异面直线 PM 与 BD 所成的角的大小为 .
【答案】 45∘
【分析】 异面直线 PM 与 BD 所成的角等于 PM 与 PN 所成的角,即为 45∘.
6. 已知点 A 是 △BCD 所在平面外一点,AD=BC,E,F 分别是 AB,CD 的中点,且 EF=22AD,求异面直线 AD 和 BC 所成的角.
【解】 如图,设 G 是 AC 的中点,连接 EG,FG 因 E,F 分别是 AB,CD 的中点.故 EG∥BC,且 EG=12BC,FG∥AD,且 FG=12AD,由异面直线所成角定义可知 EG 与 FG 所成锐角或直角为异面直线 AD,BC 所成的角,即 ∠EGF 为所求的角.
由 BC=AD 知 EG=GF=12AD,又 EF=22AD,由勾股定理可得 ∠EGF=90∘,即异面直线 AD 和 BC 所成的角为 90∘
7. 如图,正四面体 S-ABC 中,其棱长为 2.
(1)求该几何体的体积;
【解】 V=13S△ABC⋅SO=223;
(2)已知 M,N 分别是棱 AB 和 SC 的中点.求直线 BN 和直线 SM 所成的角的余弦值.
【解】 连接 MC,取 MC 中点 E,连接 BE,NE,BN,则 NE 平行于 SB.
则直线 BN 和直线 NE 所成的角即为直线 BN 和直线 SM 所成的角.
BN=3,NE=32,BE=EM2+MB2=72,cos∠BNE=BN2+NE2-BE22BN⋅NE=23,
所以直线 BN 和直线 SM 所成的角的余弦值为 23
8. 如图所示,ABCD-A1B1C1D1 是边长为 a 的正方体.
(1)求 AD1 与 B1C 所成的角的大小;
【解】 连 BC1,
则 AD1∥BC1,所以 AD1⊥B1C.即 AD1 与 B1C 所成角为 90∘.
(2)求 A1C 与 AB 所成的角的正切值;
【解】 因为 AB∥DC,所以 ∠A1CD 为 A1C 与 AB 所成的角,连 A1D,则 △A1DC 为直角三角形,所以 tan∠A1CD=A1DCD=2.
(3)若 E,F,G,H 为对应棱的中点,求 EF 与 GH 所成的角的大小.
【解】 连 AB1,B1D1,则 EF∥B1D1,GH∥AB1,即 ∠D1B1A 为 EF 与 GH 所成的角.
因为 △D1B1A 为正三角形,所以 ∠D1B1A=60∘.即 EF 与 GH 所成的角为 60∘.
9. 如图,正三棱锥 S-ABC 的侧棱与底面边长相等,E、F 分别是 SC、AB 的中点,求直线 EF 和 SA 所成的角.
【解】 设四面体各棱长均为 a,取 SB 的中点 G,FG 是 △BSA 的中位线,
则 FG∥SA,且 FG=12SA=12a,
所以 ∠GFE 就是 SA 和 EF 所成的角,
取 BC 的中点 H,连 AH,SH,如图,
则 SH⊥BC,AH⊥BC,所以 BC⊥ 平面 SAH.所以 BC⊥SA.
又因为 GF∥SA,GE∥BC,所以 FG⊥GE.
所以 △GEF 是直角三角形,且 ∠EGF=90∘,
又 GE=12a,FG=12a,所以 ∠GFE=45∘.
所以 SA 与 EF 所成的角为 45∘.
10. 如图,已知正方体 ABCD-A1B1C1D1 中,E 为 AB 的中点.
(1)求直线 B1C 与 DE 所成的角的余弦值;
【解】 连接 A1D,由 A1D∥B1C 知,B1C 与 DE 所成的角即为 A1D 与 DE 所成的角.
连接 A1E,设正方体 ABCD-A1B1C1D1 的棱长为 a,
则 A1D=2a,A1E=DE=52a,
所以 cos∠A1DE=A1D2+DE2-A1E22A1D⋅DE=105.
所以直线 B1C 与 DE 所成的角的余弦值是 105.
(2)求证:平面EB1D⊥平面B1CD.
【解】 取 B1C 的中点 F,B1D 的中点 G,连接 BF,EG,GF.
因为 CD⊥平面BCC1B1,且 BF⊂平面BCC1B1,
所以 DC⊥BF.
又因为 BF⊥B1C,CD∩B1C=C,
所以 BF⊥平面B1CD.
又因为 GF∥CD,GF=12CD,BE∥CD,BE=12CD,
所以 GF∥BE,GF=BE,
所以四边形 BFGE 是平行四边形,
所以 BF∥GE,
所以 GE⊥平面B1CD.
因为 GE⊂平面EB1D,
所以 平面EB1D⊥平面B1CD.
线面角
1. 在三棱锥 P-ABC 中,PA⊥平面ABC,∠BAC=90∘,且 D,E,F 分别是棱 AB,BC,CP 的中点,AB=AC=1,PA=2,则直线 PA 与平面 DEF 所成角为 .
【答案】 arcsin55
2. 如图,∠BAD=90∘ 的等腰直角三角形 ABD 与正三角形 CBD 所在平面成 60∘ 的二面角,则 AB 与平面 BCD 所成角的大小为 .
【答案】 arcsin64
3. 如图,在正方体 ABCD-A1B1C1D1 中,直线 A1B 和平面 A1B1CD 所成的角是 .
【答案】 30∘
4. 如图,将等腰直角三角形 ABC 沿其中位线 DE 将其折成 60∘ 的二面角 A-DE-B,则直线 AB 与平面 BCDE 所成的角的正切值是 .
【答案】 5117
5. AB∥平面α,AC⊥α 于 C,BD 是 α 的斜线,D 是斜足,若 AC=9,BD=63,则 BD 与 α 所成的角为 .
【答案】 60∘
6. 在如图所示的多面体 ABCDE 中,BA⊥ 平面 ACD,ED⊥ 平面 ACD, 且 AC=AD=CD=DE=2,AB=1.
(1)请在线段 CE 上找到点 F 的位置,使得恰有直线 BF∥ 平面 ACD,并证明这一事实;
【解】 如图,由已知 BA⊥ 平面 ACD,ED⊥ 平面 ACD,
所以 AB∥ED,
设 F 为线段 CE 的中点,
H 是线段 CD 的中点,连接 FH,
则 FH∥ED 且 FH=12ED,
所以 FH∥AB 且 FH=AB,
所以四边形 ABFH 是平行四边形,
所以 BF∥AH,
由 BF⊄ 平面 ACD 内,AH⊂ 平面 ACD,
所以 BF∥ 平面 ACD;
(2)求多面体 ABCDE 的体积;
【解】 取 AD 中点 G,连接 CG.
AB⊥ 平面 ACD,
所以 CG⊥AB,
又 CG⊥AD,
所以 CG⊥ 平面 ABED,即 CG 为四棱锥的高,
CG=3,
所以 VC-ABCD=13⋅1+22⋅2⋅3=3.
(3)求直线 EC 与平面 ABED 所成角的正弦值.
【解】 连接 EG,由(2)有 CG⊥ 平面 ABED,
所以 ∠CEG 即为直线 CE 与平面 ABED 所成的角,
设为 α,则在 Rt△CEG 中,
有 sinα=CGCE=322=64.
故直线 EC 与平面 ABED 所成角的正弦值为 64.
7. 如图,在四棱锥 P-ABCD 中,底面 ABCD 是矩形,AD⊥PD,BC=1,PC=23,PD=CD=2.
(1)求异面直线 PA 与 BC 所成角的正切值;
【解】 在四棱锥 P-ABCD 中,因为底面 ABCD 是矩形,
所以 AD=BC 且 AD∥BC,
故 ∠PAD 为异面直线 PA 与 BC 所成的角.
在 Rt△PDA 中,tan∠PAD=PDAD=2.
所以,异面直线 PA 与 BC 所成角的正切值为 2.
(2)证明:平面 PDC⊥ 平面 ABCD;
【解】 由于底面 ABCD 是矩形,
所以 AD⊥CD,
又由于 AD⊥PD,CD∩PD=D,
因此 AD⊥ 平面 PDC,
而 AD⊂ 平面 ABCD,
所以平面 PDC⊥ 平面 ABCD.
(3)求直线 PB 与平面 ABCD 所成角的正弦值.
【解】 在平面 PDC 内,过点 P 作 PE⊥CD 交直线 CD 于点 E,连接 EB.
由于平面 PDC⊥ 平面 ABCD,而直线 CD 是平面 PDC 与平面 ABCD 的交线,
则 PE⊥ 平面 ABCD,由此得 ∠PBE 为直线 PB 与平面 ABCD 所成的角.
在 △PDC 中,由于 PD=CD=2,PC=23,可得 ∠PCD=30∘.
在 Rt△PEC 中,PE=PCsin30∘=3.
由 AD∥BC,AD⊥ 平面 PDC,得 BC⊥ 平面 PDC,因此 BC⊥PC.
在 Rt△PCB 中,PB=PC2+BC2=13.
在 Rt△PEB 中,sin∠PBE=PEPB=3913.
所以直线 PB 与平面 ABCD 所成角的正弦值为 3913.
8. 如图,梯形 ABCD 中,CD∥AB,AD=DC=CB=12AB,E 是 AB 的中点,将 △ADE 沿 DE 折起,使点 A 折到点 P 的位置,且二面角 P-DE-C 的大小为 120∘.
(1)求证:DE∥平面PBC;
【解】 因为 E 是 AB 的中点,所以 BE=12AB.
又因为 CD∥AB,DC=12AB,所以 DC∥EB 且 DC=EB.
所以,四边形 DCBE 是平行四边形,所以 ED∥BC.
因为 DE⊄平面PBC,BC⊂平面PBC,所以 DE∥ 平面 PBC.
(2)求证:DE⊥PC;
【解】
连接 EC,据(1)知,CD∥AE 且 CD=AE,所以,四边形 ADCE 为平行四边形,又 AD=DC,所以,四边形 ADCE 是菱形.连接 AC 交 DE 于 F,连接 PF,则 DE⊥AC,DE⊥PF,因为 AC∩PF=F,所以 DE⊥平面PFC.
又因为 PC⊂平面PFC,所以 DE⊥PC.
(3)求直线 PD 与平面 BCDE 所成角的正弦值.
【解】 因为 DE⊥平面PFC,DE⊂平面BCDE,
所以,平面 PFC⊥平面BCDE,且两平面交于 AC.
过点 P 作 PH⊥AC 于 H,则 PH⊥平面BCDE,连接 DH,则 DH 为 PD 在平面 BCDE 上的射影,所以 ∠PDH 就是直线 PD 与平面 BCDE 所成的角.由(2)知,∠PFC 就是二面角 P-DE-C 的平面角,所以 ∠PFC=120∘,所以 ∠PFA=60∘.设 AD=AE=BC=DE=a,则 AF=PF=32a.
在 Rt△PHF 中,PH=PF⋅sin60∘=34a.所以,在 Rt△PHD 中,sin∠PDH=PHPD=34.
9. 已知在四棱锥 P一ABCD 中,底面 ABCD 是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F 分别是 AB,PD 的中点.
(1)求证:AF∥平面PEC;
【解】 取 PC 的中点 O,连接 OF,OE.
所以 FO∥DC,且 FO=12DC,
所以 FO∥AE,
又 E 是 AB 的中点,且 AB=DC,
所以 FO=AE,
所以四边形 AEOF 是平行四边形,
所以 AF∥OE,
又 OE⊂平面PEC,AF⊄平面PEC,
所以 AF∥平面PEC.
(2)求 PC 与 平面ABCD 所成角的正切值;
【解】 连接 AC
因为 PA⊥平面ABCD,
所以 ∠PCA 是直线 PC 与平面 ABCD 所成的角,
在 Rt△PAC 中 tan∠PCA=PAAC=15=55,
即直线 PC 与 平面ABCD 所成的角正切为 55.
(3)求 二面角P-EC-D 的正切值.
【解】 作 AM⊥CE,交 CE 的延长线于 M.
连接 PM,
由三垂线定理,得 PM⊥CE,
所以 ∠PMA 是二面角 P-EC-D 的平面角
由 △AME∽△CBE,
可得 AM=22,
所以 tan∠PMA=PAAM=2,
所以 二面角 P-EC-D 的正切为 2.
10. 如图所示,四棱锥 P-ABCD 中,AB⊥AD,AD⊥DC,PA⊥ 底面 ABCD,PA=AD=DC=12AB=1,M 为 PC 的中点,N 点在 AB 上且 AN=13NB.
(1)证明:MN∥平面PAD;
【解】 如图,过 M 作 ME∥CD,交 PD 于 E,连接 AE.
∵ AN=13NB,∴ AN=14AB=12DC=EM.
又 EM∥DC∥AB,∴ EM 平行且等于 AN,∴ AEMN 为平行四边形.
∴ MN∥AE.又 AE⊂平面PAD,
∴ MN∥平面PAD.
(2)求直线 MN 与平面 PCB 所成的角.
【解】 如图,过点 N 作 NQ∥AP,交 BP 于点 Q,NF⊥CB 于点 F,
连接 QF,过 N 点作 NH⊥QF,交 QF 于点 H,连接 MH.
易知 QN⊥平面ABCD,∴ QN⊥BC,而 NF⊥BC,∴ BC⊥平面QNF,
∴ BC⊥NH,而 NH⊥QF,QF∩BC=F,∴ NH⊥平面PBC,
∴ ∠NMH 为直线 MN 与平面 PCB 所成的角.
通过计算可得 MN=AE=22,QN=34,NF=342,
∴ NH=QN⋅NFQF=QN⋅NFQN2+NF2=64,
∴ sin∠NMH=NHMN=32,∴ ∠NMH=60∘.
∴ 直线 MN 与平面 PCB 所成的角为 60∘.
二面角
1. A 是锐二面角 α-l-β 的 α 内一点,AB⊥β 于点 B,AB=3,A 到 l 的距离为 2,则二面角 α-l-β 的平面角大小 .
【答案】 60∘
2. 棱长都相等的三棱锥(即正四面体)ABCD 中,相邻两个平面所成的二面角的余弦值为 .
【答案】 13
【分析】 取 BC 的中点 E,连接 AE,DE,因为四面体 ABCD 是正四面体,所以 BC⊥AE,BC⊥ED,所以 ∠AED 为二面角 A-BC-D 的平面角.
设正四面体的棱长为 1,则 AE=32,DE=32,AD=1,在 △ADE 中可求得 cos∠AED=13.
3. 如图二面角 α-AB-β 内一点 P 到平面 α 的距离为 PC=1,到平面 β 的距离为 PD=3,且 CD=7,则二面角 α-AB-β 的大小为 .
【答案】 120∘
4. 在长方形 ABCD 中,AB=3,BC=1,E 为 DC 的三等分点(靠近 C 处),F 为线段 EC 上一动点(包括端点),现将 △AFD 沿 AF 折起,使 D 点在平面内的射影恰好落在边 AB 上,则当 F 运动时,二面角 D-AF-B 平面角余弦值的变化范围是 .
【答案】 19,14
【分析】 如图,过点 D 作 DM⊥AF 于点 O,交 AB 于点 M,不妨设二面角 D-AF-B 为 θ,则 cosθ=OMOD,设 DF=x,2⩽x⩽3,
由勾股定理,OD=xx2+1,OF=x4x2+1,OA=1x2+1,
所以 cosθ=OMOD=OAOF=1x2 在 2,3 上是减函数,
解得 19⩽cosθ⩽14.
5. 如图,矩形 ABCD 中,DC=3,AD=1,在 DC 上截取 DE=1,将 △ADE 沿 AE 翻折到 △AD1E,当点 D1 在平面 ABC 上的射影落在 AC 上时,二面角 D1-AE-B 的平面角的余弦值是 .
【答案】 2-3
【分析】 令点 D1 在平面 ABC 上的射影为 G,过 D1 作 D1F⊥AE 于 F,连接 GF,则 ∠D1FG 即为二面角 D1-AE-B 的平面角,又因为 DC=3,AD=1,D1E=1,所以 D1F=AF=22,∠FAG=15∘,则 FG=22tan15∘,则 cos∠D1FG=FGD1F=2-3.
6. 如图,平面ABCD⊥平面ADEF,其中 ABCD 为矩形,ADEF 为梯形,AF∥DE,AF⊥FE,AF=AD=2,DE=1.
(1)求异面直线 EF 与 BC 所成角的大小;
【解】 延长 AD,FE 交于 Q.
因为 ABCD 是矩形,
所以 BC∥AD,
所以 ∠AQF 是异面直线 EF 与 BC 所成的角.
在梯形 ADEF 中,由 DE∥AF,AF⊥FE,AF=2,DE=1,
得 ∠AQF=30∘.
即异面直线 EF 与 BC 所成角为 30∘.
(2)若二面角 A-BF-D 的平面角的余弦值为 13,求 CF 的长.
【解】 设 AB=x.取 AF 的中点 G.
由题意,得 DG⊥AF.
因为 平面ABCD⊥平面ADEF,AB⊥AD,
所以 AB⊥平面ADEF,
从而 AB⊥DG.
所以 DG⊥平面ABF.
过 G 作 GH⊥BF,垂足为 H,连接 DH,则 DH⊥BF,
则 ∠DHG 为二面角 A-BF-D 的平面角.
在直角 △AGD 中,AD=2,AG=1,得 DG=3.
在直角 △BAF 中,由 ABBF=sin∠AFB=GHFG,得 GHx=1x2+4,
解得 GH=xx2+4.
在直角 △DGH 中,DG=3,GH=xx2+4,则 DH=2x2+3x2+4.
由 cos∠DHG=GHDH=13,解得 x=2515,
即 AB=2515.
因为 AF⊥FE,AF=AD=2,DE=1,
所以 AF=AD=DF=2,
因此 CF=CD2+DF2=6025+4=4105.
7. 如图所示,四面体 P-ABC 中,AP,AB,AC 两两垂直,且 PA=2,AB=3,AC=4,求二面角 P-BC-A 的正切值.
【解】 因为 PA,AB,AC 两两垂直,所以 PA⊥ 平面 ABC.
过 A 作 AD⊥BC 于 D,连接 PD,则 BC⊥ 平面 PAD,所以 PD⊥BC.
根据二面角的平面角定义,∠PDA 为所求的角.
在 Rt△ABC 中,AB=3,AC=4,所以 BC=5.
又 12AB⋅AC=12BC⋅AD,可求得 AD=125.
所以 tan∠PDA=PAAD=2125=56.
8. 在四棱锥 P-ABCD 中,底面 ABCD 是正方形,侧棱PD⊥平面ABCD,PD=DC,E 是 PC 中点,作 EF⊥PB 交 PB 于点 F.
(1)证明:PB⊥平面EFD;
【解】 因为 PD⊥底面ABCD 且 DC,BC⊂底面ABCD,
所以 PD⊥DC,PD⊥BC.
又 PD=DC,
所以 △PDC 是等腰直角三角形,而 DE 是斜边 PC 的中线,
所以 DE⊥PC.
因为底面 ABCD 是正方形,
所以 DC⊥BC,
又因为 DC∩PD=D,
所以 BC⊥平面PDC.
而 DE⊂平面PDC,
所以 BC⊥DE,
由①和②推得 DE⊥平面PBC.
而 PB⊂平面PBC,
所以 PB⊥DE.
又 EF⊥PB 且 DE∩EF=E,
所以 PB⊥平面EFD.
(2)求二面角 C-PB-D 的大小.
【解】 由(1)知 PB⊥DF,故 ∠EFD 是二面角 C-PB-D 的平面角.
由(1)知 DE⊥EF,PD⊥DB.
设正方形 ABCD 的边长为 α,则 PD=DC=a,BD=2a,BP=PD2+BD2=3a,PC=PD2+DC2=2a,DE=12PC=22a,
在 Rt△PDB 中,DF=PD⋅BDPB=a⋅2a3a=63a,
在 Rt△EFD 中,sin∠EFD=DEDF=32,
所以 ∠EFD=60∘,即二面角 C-PB-D 的大小为 60∘.
9. 如图,在四棱锥 P-ABCD 中,PD⊥平面ABCD,△ABC 是边长为 1 正三角形,CD=DA=33,AC 与 BD 的交点为 M,点 N 在线段 PB 上,且 PN=12.若二面角 A-BC-P 的正切值为 22.
(1)求证:MN∥平面PDC;
【解】 在 △ACD 中,由余弦定理可以求出 ∠ADC=2π3,所以 ∠BCD=∠BCA+∠DCA=π2.
又因为 PD⊥平面ABCD,所以 PD⊥BC,所以 BC⊥平面PDC.
所以 BC⊥CD,BC⊥PC,所以 ∠PCD 为二面角 A-BC-P 的平面角,所以 tan∠PCD=22.
因为 CD=33,所以 PD=263.
因为 BD=BM+MD=32+36=233,所以 PB=2.
PNPB=14=MDBD,所以 MN∥PD,又因为 MN⊄平面PDC,PD⊂平面PDC,
所以 MN∥平面PDC.
(2)求平面 DCP 与平面 ABP 所成的锐角的余弦值.
【解】 分别延长 CD,AB 交于点 G,则 PG 为两个平面的棱,作 CE⊥PG,连接 BE.
因为 BC⊥平面PDC,所以 BC⊥PG,所以 PG⊥平面BEC,所以 BE⊥PG,
所以 ∠CEB 为平面 DCP 与平面 ABP 所成的锐平面角.
易求出 CE=2,BE=3,所以 cos∠CEB=23=63,
所以平面 DCP 与平面 ABP 所成的锐角的余弦值 63.
10. 在正三角形 ABC 中,E 、 F 、 P 分别是 AB 、 AC 、 BC 边上的点,满足 AE:EB=CF:FA=CP:PB=1:2(如图 1).将 △AEF 沿 EF 折起到 △A1EF 的位置,使二面角 A1-EF-B 成直二面角,连结 A1B 、 A1P(如图 2).
(1)求证:A1E⊥平面 BEP;
【解】 不妨设正三角形 ABC 的边长为 3,则在图 1 中,取 BE 的中点 D,连结 DF.
∵ AE∶EB=CF∶FA=1∶2,
∴ AF=AD=2,而 ∠A=60∘,
∴ △ADF 为正三角形.
又 AE=DE=1,∴ EF⊥AE.
从而在图 2 中,EF⊥A1E.
∵ 二面角 A1-EF-B 为直二面角,
∴ A1E⊥平面 BEP.
(2)求直线 A1E 与平面 A1BP 所成角的大小;
【解】 在图 2 中,∵ A1E⊥平面 BEP,
∴ A1E⊥BP,
由线面垂直的判定与性质,得 BP 垂直于 A1E 在面 A1BP 内的射影.
设 A1E 在平面 A1BP 内的射影为 A1Q,且 A1Q 交 BP 于 Q.
则 ∠EA1Q 就是 A1E 与平面 A1BP 所成的角,且 BP⊥A1Q.
在 △EBP 中,∵ BE=BP=2,∠EBP=60∘,
∴ △EBP 为正三角形,∴ BE=EP.
又 ∵ A1E⊥平面 BEP,∴ A1B=A1P,
∴ Q 为 BP 的中点,且 EQ=3,而 A1E=1,
∴ 在 Rt△A1EQ 中,
tan∠EA1Q=EQA1E=3.
因此,直线 A1E 与面 A1BP 所成角为 60∘.
(3)求二面角 B-A1P-F 的大小.(用反三角函数表示)
【解】
在图 2 中,过 F 作 FM⊥A1P 于 M,连结 QM 、 QF.
∵ CF=CP=1,∠C=60∘,
∴ △FCP 为正三角形,从而 PF=1.
又 ∵ PQ=12BP=1,∴ PF=PQ.⋯⋯①
∵ A1E⊥平面BEP,EQ=EF=3,
∴ A1F=A1Q,
∴ △A1FP≅△A1QP,从而 ∠A1PF=∠A1PQ.⋯⋯②
由 ①、② 及 MP 为公共边,得 △FMP≅△QMP,
∴ ∠QMP=∠FMP=90∘,且 MF=MQ,
从而 ∠FMQ 为二面角 B-A1P-F 的平面角.
在 Rt△A1QP 中,A1Q=A1F=2,PQ=1,∴ A1P=5.
由 MQ⊥A1P,得
MF=MQ=A1Q⋅PQA1P=255.
在 △FCQ 中,FC=1,QC=2,∠C=60∘.
由余弦定理,得 QF=3,
在 △FMQ 中,
cos∠FMQ=MF2+MQ2-QF22MF⋅MQ=-78.
因此,二面角 B-A1P-F 的大小为 π-arccos78.
课后练习
1. 已知正四棱锥的所有棱长均相等,则侧面与底面所成二面角的余弦值为 .
2. 如图,在棱长为 1 的正方体 ABCD-A1B1C1D1 中,点 E,F 分别是棱 BC,CC1 的中点,P 是侧面 BCC1B1 内一点,若 A1P∥平面AEF,则线段 A1P 长度的取值范围是 .
3. 如图,在矩形 ABCD 中,若 AB=15,BC=20,PA⊥平面ABCD,且 PA=5,则点 P 到直线 BD 的距离为 .
4. ∠AOB 在平面 α 内,OC 是平面 α 的一条斜线,若 ∠AOB=∠BOC=∠COA=θ90∘<θ<120∘,则 OC 与平面 α 所成角的余弦值是 .
5. 正方形 ABCD 与 ABEF 的边长都为 a,若二面角 E-AB-C 的大小为 30∘,则 EF 与平面 ABCD 的距离为 .
6. 棱长为 4 的正方体相邻两个面的中心之间的距离为 .
7. 空间四边形 ABCD 中,若 AB=BC=CD=DA=BD=1,则 AC 的取值范围是 .
8. 如图,若边长为 a 的正方形 ABCD 和正方形 ABEF 所在平面互相垂直,M,N 分别在对角线 AC,BF 上,且 AM=NF,则线段 MN 的最小值为 .
9. 地面上有两根相距 a 米的旗杆,它们的高分别是 b 米和 c 米 b>c,则它们上端的距离为 .
10. 如图,正方体 ABCD-A1B1C1D1 中, AB=2 ,点 E 为 AD 的中点,点 F 在 CD 上,若 EF∥平面 AB1C ,则线段 EF 的长度等于 .
11. A,B 两点到平面 α 的距离分别是 3 cm,5 cm,点 M 是 AB 的中点,则 M 点到平面 α 的距离是 .
12. 如图,在 60∘ 的二面角 α-l-β 内取点 A,在半平面 α,β 中分别任取点 B,C.若 A 到棱 l 的距离为 1,则 △ABC 的周长的最小值为 .
13. △ABC 的三个顶点 A 、 B 、 C 到平面 α 的距离分别为 2 cm 、 3 cm 、 4 cm,且它们在 α 的同侧,则 △ABC 的重心到平面 α 的距离为 .
14. A、B 两点到平面 α 的距离分别是 3 cm 、 5 cm,M 点是 AB 的中点,则 M 点到平面的距离是 .
15. 在棱长为 1 的正方体 ABCD—AʹBʹCʹDʹ 中,M 为体对角线 BDʹ 上动点,则 M 到 CCʹ 距离的最小值为 ;M 位于 BDʹ 三等分点处时,M 到各顶点的距离的不同取值有 种.
16. 在三棱锥 P-ABC 中,PA⊥底面ABC,AC⊥BC,PA=AC=BC=2,则直线 PC 与 AB 所成角的大小是 .
17. 在正方体 ABCD-A1B1C1D1 中,M 是 AB 的中点,则 sin 的值等于 .
18. 如图,在正方体 ABCD-A1B1C1D1 中, M,N 分别是 CD,CC1 的中点,则异面直线 A1M 与 DN 所成角的大小是 .
19. 正方体 ABCD-A1B1C1D1 中,B1D 与 BC1 夹角的大小是 ;若 E,F 分别为 AB,CC1 的中点,则异面直线 EF 与 A1C1 夹角的大小是 .
20. 已知正方体 ABCD-A1B1C1D1 中,E 为 C1D1 的中点,则异面直线 AE 与 BC 所成角的余弦值为 .
21. 如图,在三棱锥 P-ABC 中,PA=PB=PC=BC,且 ∠BAC=π2,则 PA 与底面 ABC 所成角为 .
22. 已知 ∠AOB=90∘,C 为空间中一点,且 ∠AOC=∠BOC=60∘,则直线 OC 与平面 AOB 所成角的正弦值为 .
23. 已知三棱柱 ABC-A1B1C1 的侧棱与底面边长都相等,A1 在底面 ABC 上的射影为 △ABC 的中心,则直线 AB1 与底面 ABC 所成的角的正弦值为 .
24. 如图所示,A 是直二面角 α-EF-β 的棱 EF 上的点,AB,AC 分别是 α,β 内的射线,∠EAB=∠EAC=45∘,则 ∠BAC= .
25. 正方体 ABCD-A1B1C1D1 中,二面角 A1-BC1-D1 的正切值为 .
26. 如图,四棱锥 P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=PA=2,CD=4,E,F 分别是 PC,PD 的中点.
(1)证明:EF∥平面PAB;
(2)求直线 AC 与平面 ABEF 所成角的正弦值.
27. 正四棱锥的高为 3,侧棱长为 7,求侧面上斜高的长.
28. 在大小为 120∘ 的二面角的棱上,有两个点 A,B,且 AC,BD 分别是在这个二面角的两个面内垂直于 AB 的线段,已知 AB=4 cm,AC=6 cm,BD=8 cm.求 CD 的长.
29. 若平面 α 内的直角 △ABC 的斜边 AB=20,α 外一点 P 到 A,B,C 三点的距离都是 25,求点 P 到 α 的距离.
30. 如图,长方体 ABCD-A1B1C1D1 中,AB=2,BC=CC1=1,点 P 是 CD 上的一点,PC=λPD.
(1)若 A1C⊥平面PBC1,求 λ 的值;
(2)设 λ1=1,λ2=3 所对应的点 P 为 P1,P2,二面角 P1-BC1-P2 的大小为 θ,求 cosθ 的值.
31. 如图所示,已知两个正方形 ABCD 和 DCEF 不在同一平面内,M,N 分别为 AB,DF 的中点.若 CD=2,平面ABCD⊥平面DCEF,求 MN 的长.
32. 长方体 ABCD-A1B1C1D1 的一条对角线 AC1=82,∠C1AA1=45∘,∠C1AB=60∘,求 AD 的长.
33. 如图所示,平面α⊥平面β,在 α 与 β 的交线 l 上取线段 AB=4 cm,AC,BD 分别在平面 α 和平面 β 内,AC⊥l,BD⊥l,AC=3 cm,BD=12 cm,求线段 CD 的长.
34. 如图,在四面体 PABC 中,PC⊥AB,PA⊥BC,点 D,E,F,G 分别是棱 AP,AC,BC,PB 的中点.
(1)求证:DE∥ 平面 BCP;
(2)求证:四边形 DEFG 为矩形;
(3)是否存在点 Q,到四面体 PABC 六条棱的中点的距离相等?说明理由.
35. 在直三棱柱 ABC-A1B1C1 的底面 △ABC 中,CA=CB=1,∠BCA=90∘,棱 AA1=2,M,N 分别是 A1B1,A1A 的中点,求 MN 的长.
36. 如图,已知直三棱柱 ABC-A1B1C1 中, AC⊥BC ,侧面 BCC1B1 是边长为 a 的正方形, D 、 E 分别是 B1C1 、 BB1 的中点.
(1)试过 A,C,D 三点作出该三棱柱的截面,并说明理由;
(2)求证: C1E⊥截面 ACD ;
(3)求点 B1 到截面 ACD 的距离.
37. 如图所示,在直三棱柱 ABC-A1B1C1 中,∠ACB=90∘,AC=BC=a,D,E 分别为棱 AB,BC 的中点,M 为棱 AA1 上的点,二面角 M-DE-A 为 30∘.
(1)证明:A1B1⊥C1D;
(2)求 MA 的长,并求点 C 到平面 MDE 的距离.
38. 如图,正三棱柱 ABC-A1B1C1 中,D 是 BC 的中点,AB=a.
(1)求证:直线 A1D⊥B1C1;
(2)求点 D 到平面 ACC1 的距离;
(3)判断 A1B 与平面 ADC1 的位置关系,并证明你的结论.
39. 如图,已知 P 为 △ABC 外一点,PA,PB,PC 两两垂直,PA=PB=PC=a,求点 P 到平面 ABC 的距离.
40. 如图,在长方体 ABCD-AʹBʹCʹDʹ 中,AB=2,AD=1,AAʹ=1,证明直线 BCʹ 平行于平面 DʹAC,并求直线 BCʹ 到平面 DʹAC 的距离.
41. 已知 ABCD-A1B1C1D1 是底面边长为 1 的正四棱柱,高 AA1=2,求
(1)异面直线 BD 与 AB1 所成角的余弦值;
(2)四面体 AB1D1C 的体积.
42. 如图,圆锥的顶点为 P,底面圆心为 O,底面的一条直径为 AB,C 为半圆弧 AB 的中点,E 为劣弧 CB 的中点,已知 PO=2,OA=1,求三棱锥 P-AOC 的体积,并求异面直线 PA 与 OE 所成角的余弦值.
43. 如图’在正方体 ABCD-A1B1C1D1 中,点 E1,F1 分别在 A1B1,C1D1 上.且 E1B1=14A1B1,D1F1=14D1C1,求 BE1 与 DF1 所成的角的大小.
44. 如图所示,在空间四边形 OABC 中,OA=8,AB=6,AC=4,BC=5,∠OAC=45∘,∠OAB=60∘,求 OA 与 BC 所成角的余弦值.
45. 如图所示,等腰直角三角形 ABC 中,∠BAC=90∘,BC=2,DA⊥AC,DA⊥AB,若 DA=1,且 E 为 DA 的中点,求异面直线 BE 与 CD 所成角的余弦值.
46. 如图,ABCD 是矩形,PA⊥平面ABCD,PA=AD=a,AB=2a,E 是线段 PD 上的店,F 是线段 AB 上的点,且 PEED=BFFA=12.求直线 EF 与平面 ABCD 所成角的正弦值.
47. 如图所示,在正方体 ABCD-A1B1C1D1 中, E 是棱 DD1 的中点.
(1)求直线 BE 和平面 ABB1A1 所成的角的正弦值;
(2)在棱 C1D1 上是否存在一点 F ,使 B1F∥平面A1BE ?证明你的结论.
48. 如图,已知三角形 △ABC 与 △BCD 所在平面互相垂直,且 ∠BAC=∠BCD=90∘,AB=AC,CB=CD,点 P,Q 分别在线段 BD,CD 上,沿直线 PQ 将 △PQD 向上翻折,使 D 与 A 重合.
(1)求证:AB⊥CQ;
(2)求直线 AP 与平面 ACQ 所成的角.
49. 如图,在三棱锥 P-ABC 中,AB=AC,D 为 BC 的中点,PO ⊥平面 ABC,垂足 O 落在线段 AD 上.
(1)证明:AP⊥BC;
(2)已知 BC=8,PO=4,AO=3,OD=2.求二面角 B-AP-C 的大小.
50. 如图,ABCD-A1B1C1D1 是正四棱柱,侧棱长为 1,底面边长为 2,E 是棱 BC 的中点.
(1)求三棱锥 D1-DBC 的体积;
(2)证明 BD1∥ 平面 C1DE;
(3)求面 C1DE 与面 CDE 所成二面角的正切值.
空间几何量-出门考
姓名 成绩
1. 如图所示,在长方体 ABCD-A1B1C1D1 中,AB=BC=2,AA1=1,则 BC1 与平面 BB1D1D 所成角的正弦值为 .
2. 把正方形 ABCD 沿对角线 AC 折起,当以 A,B,C,D 四点为顶点的三棱锥体积最大时,直线 BD 和平面 ABC 所成的角的大小为 .
3. 三棱锥 P-ABC 中,PA=PB=PC=73,AB=10,BC=8,CA=6,则二面角 P-AC-B 的余弦值为 .
4. 作等腰直角三角形 ABC 的斜边 AB 的中线 CD,沿 CD 将 △ABC 折叠,使平面 ACD ⊥ 平面 BCD,则折叠后 AC 与 BC 的夹角 ∠ACB 的度数为 .
5. A 是 △BCD 所在平面外一点,M,N 分别是 △ABC,△ACD 的重心,若 BC=6,则 MN= .
6. 如图,四边形 ABCD-A1B1C1D1 的棱长为 1,BD∩AC=O,M 是线段 D1O 上的动点,过点 M 作平面 ACD1 的垂线交平面 A1B1C1D1 于点 N,则点 N 到点 A 距离的最小值为 .
7. 若构成教室墙角的三个墙面记为 α,β,γ,交线记为 BA,BC,BD,教室内一点 P 到三墙面 α,β,γ 的距离分别为 3 m 、 4 m 、 1 m,则 P 与墙角 B 的距离为 m.
8. 在直三棱柱 A1B1C1-ABC 中,底面 ABC 为直角三角形,∠BAC=π2,AB=AC=AA1=1.已知 G 与 E 分别为 A1B1 和 CC1 的中点,D 与 F 分别为线段 AC 和 AB 上的动点(不包括端点).若 GD⊥EF,则线段 DF 的长度的最小值为 .
9. 自半径为 R 的球面上一点 Q,作球的互相垂直的三条弦 AQ,QB,QC,则 QA2+QB2+QC2= (用 R 表示).
10. 若两点的坐标是 A3cosα,3sinα,1,B2cosθ,2sinθ,1,则 ∣AB∣ 的取值范围是 .
11. 如图,直线 l,g 分别被三个平行平面 α,β,γ 所截,交点依次为 A,B,C,D,E,F,已知 AB=2,BC=3,EF=4,则 DF= .
12. 一件工艺品是将一个彩色半透明的正四面体镶嵌于一个水晶球体内制作而成的.已知正四面体的顶点都在球面上,球的直径为 12 cm,则正四面体的棱长为 cm,球心到正四面体各面的距离为 cm.
13. 在 △ABC 中,∠ACB=90∘,AB=8,∠ABC=60∘,PC⊥平面ABC,PC=4,M 是 AB 上一个动点,则 PM 的最小值为 .
14. 已知长方体 A1B1C1D1-ABCD 中,棱 AA1=5,AB=12,那么直线 B1C1 到平面 A1BCD1 的距离是 .
15. 已知直三棱柱 ABC-A1B1C1 中,∠ABC=90∘,AC=AA1=22,AB=2,M 为 BB1 的中点,则 B1 与平面 ACM 的距离为 .
16. 在正三棱柱 ABC-A1B1C1 中,AA1=3AB,则异面直线 A1B 与 CC1 所成的角的大小是 .
17. 如图,已知圆柱的母线 BC 长为 l,底面半径为 r,O 是上底面圆心,A,B 是下底面圆周上两个不同的点,若直线 OA 与 BC 所成角的大小为 π6,则 lr= .
18. 如图,在直三棱柱 ABC-A1B1C1 中,AB=BC=CC1=2,AC=23,M 是 AC 的中点,则异面直线 CB1 与 C1M 所成角的余弦值为 .
19. 在已知四面体 ABCD 中, E 、 F 分别是 BC 、 AD 中点, EF=5 , AB=8 , CD=6 ,则 AB 与 CD 所成的角的大小 .
20. 如图所示,六棱柱 ABCDEF-A1B1C1D1E1F1 中,底面是正六边形.
(1)A1F1 与 BD 所成角的度数为 .
(2)C1F1 与 BE 所成角的度数为 .
21. 在正方体 ABCD-A1B1C1D1 中,BD1 与平面 A1B1C1D1 所成角的正切值为 .
22. 已知正四棱柱 ABCD-A1B1C1D1 中,AA1=2AB,则 CD 与平面 BDC1 所成角的正弦值为 .
23. 在正方体 ABCD-A1B1C1D1 中,直线 BD1 与平面 ABCD 所成的角的余弦值为 .
24. 在正方体 ABCD-A1B1C1D1 中,二面角 D1-AC-D 的正切值是 .
25. 正方体 ABCD-A1B1C1D1 中,二面角 B1-AD-B 的平面角等于 .
26. 如图(1),在等腰梯形 CDEF 中,CB,DA 是梯形的高,AE=BF=2,AB=22,现将梯形沿 CB,DA 折起,使 EF∥AB 且 EF=2AB,得一简单组合体 ABCDEF 如图(2)示,已知 M,N 分别为 AF,BD 的中点.
(1)求证:MN∥平面BCF;
(2)若直线 DE 与平面 ABCD 所成角的正切值为 22,求平面 CDEF 与平面 ADE 所成的锐二面角大小.
27. 已知圆锥的底面半径为 r,高为 h,正方体 ABCD-A1B1C1D1 内接于圆锥,求这个正方体的棱长.
28. 正方体 ABCD-A1B1C1D1 中.
(1)求 AC 与 A1D 所成角的大小;
(2)若 E 、 F 分别为 AB 、 AD 的中点,求 A1C1 与 EF 所成角的大小.
29. 将边长为 1 的正方形 AA1O1O(及其内部)绕边 OO1 旋转一周形成圆柱,如图,AC⌢ 长为 23π,A1B1⌢ 长为 π3,其中 B1 与 C 在平面 AA1O1O 的同侧.
(1)求三棱锥 C-O1A1B1 的体积;
(2)求异面直线 B1C 与 AA1 所成的角的大小.
30. 如图,正三角形 ABC 的边长为 3,过其中心 G 作 BC 边的平行线,分别交 AB,AC 于 B1,C1.将 △AB1C1 沿 B1C1 折起到 △A1B1C1 的位置,使点 A1 在平面 BB1C1C 上的射影恰是线段 BC 的中点 M.求:二面角 A1-B1C1-M 的大小.
31. 如图,在棱长为 1 的正方体 ABCD-AʹBʹCʹDʹ 中,M,N 分别是 AʹB,AC 上的点,且 AʹM=AN.
(1)求证:MN∣∣平面BBʹCʹC.
(2)当 AN=a 时,求 MN 的长.
(3)当 a 为何值时,MN 最短,并求出 MN 的最小值.
32. 如图,AB 是圆 O 的直径,点 C 是圆 O 上异于 A,B 的点,PO 垂直于圆 O 所在的平面,且 PO=OB=1.
(1)求三棱锥 P-ABC 体积的最大值;
(2)若 BC=2,点 E 在线段 PB 上,求 CE+OE 的最小值.
33. 如图,四棱锥 P-ABCD 中,PA⊥ 底面 ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=π3,F 为 PC 的中点,AF⊥PB.
(1)求 PA 的长;
(2)求二面角 B-AF-D 的正弦值.
34. 已知正四面体 ABCD,各棱长为 1,M,N 分别是 AB,CD 的中点,求 MN 的长和点 A 到面 BCD 的距离.
35. 如图,空间直角坐标系中有一个正方体 A1B1C1D1-ABCD,它的棱长为 a,M,N 分别是 BC1,AC 上的点,且 ∣AN∣=2∣NC∣,∣BM∣=2∣MC1∣,求 MN 的长.
36. 如图,ABCD 是平行四边形,已知 AB=2BC=4,BD=23,BE=CE,平面 BCE⊥平面ABCD.
(1)证明:BD⊥CE.
(2)若 BE=CE=10,求三棱锥 B-ADE 的高.
37. 如图,已知平面 A1B1C1 平行于三棱锥 V-ABC 的底面 ABC,等边 △AB1C 所在的平面与底面 ABC 垂直,且 ∠ACB=90∘,设 AC=2a,BC=a.
(1)求证直线 B1C1 是异面直线 AB1 与 A1C1 的公垂线;
(2)求点 A 到平面 VBC 的距离;
(3)求二面角 A-VB-C 的大小.
38. 如图,边长为 1 的正方体 ABCD-A1B1C1D1 中,E,F 分别为 BB1,C1C 的中点,DG=13DD1,过 E,F,G 的平面交 AA1 于点 H,求 A1D1 到面 EFGH 的距离.
39. 如图,已知两个正四棱锥 P-ABCD 与 Q-ABCD 的高分别为 1 和 2,AB=4.
(1)证明:PQ⊥平面 ABCD;
(2)求异面直线 AQ 与 PB 所成的角;
(3)求点 P 到平面 QAD 的距离.
40. 正方体 ABCD-A1B1C1D1 的各边长为 1,求 平面A1BD 与 平面B1CD1 间的距离.
41. 如图所示,为了制作一个圆柱形灯笼,先要制作 4 个全等的矩形骨架,总计耗用 9.6 米铁丝.骨架将圆柱底面 8 等分.再用 S 平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
(1)当圆柱底面半径 r 取何值时,S 取得最大值?并求出该最大值(结果精确到 0.01 平方米);
(2)在灯笼内,以矩形骨架的顶点为端点,安装一些霓虹灯.当灯笼底面半径为 0.3 米时,求图中两根直线型霓虹灯 A1B3 、 A3B5 所在异面直线所成角的的余弦值.
42. 已知矩形 ABCD 内接于圆柱下底面的圆 O,PA 是圆柱的母线,若 AB=6,AD=8,异面直线 PB 与 CD 所成的角为 arctan2,求此圆柱的体积.
43. 如图,四边形 ABCD 为矩形,PD⊥平面ABCD,PD=DC=2,BC=2,E 是 PC 的中点.
(1)证明:PA∥平面EDB;
(2)求异面直线 AD 与 BE 所成角的大小.
44. 如图,在正方体 ABCD-A1B1C1D1 中,E,F 分别是 BB1,DC 的中点.
(1)求 AE 与 D1F 所成的角;
(2)求证:AE⊥平面A1D1F.
45. 如图,在正方体 ABCD-A1B1C1D1 中,E,F 分别是 BB1,CD 的中点.
(1)证明 AD⊥D1F;
(2)求 AE 与 D1F 所成的角;
(3)证明 面AED⊥面A1FD1;
(4)设 AA1=2,求三棱锥 F-A1ED1 的体积 VF-A1ED1.
46. 如图,在侧棱垂直底面的四棱柱 ABCD-A1B1C1D1 中,AD∥BC,AD⊥AB,AB=2,AD=2,BC=4,AA1=2,E 是 DD1 的中点,F 是平面 B1C1E 与直线 AA1 的交点.
(1)证明:
(i)EF∥A1D1;
(ii)BA1⊥ 平面 B1C1EF;
(2)求 BC1 与平面 B1C1EF 所成的角的正弦值.
47. 如图,正三棱柱 ABC-A1B1C1 的底面边长为 a,侧棱长为 2a,M 是 A1B1 的中点.
(1)求证:MC1 是平面 ABB1A1 的一个法向量;
(2)求 AC1 与侧面 ABB1A1 所成的角.
48. 如图,四面体 ABCS 中,SA,SB,SC 两两垂直,∠ABS=45∘,∠ABC=60∘,M 为 AB 的中点.
(1)求 BC 与平面 SAB 所成的角;
(2)求证:平面 ABC⊥ 平面 SCM;
(3)求 SC 与平面 ABC 所成角的正弦值.
49. 已知正方体 ABCD-A1B1C1D1 的棱长为 2,P,Q 分别是 BC,CD 上的动点,且 ∣PQ∣=2,建立如图所示的坐标系:
(1)确定 P,Q 的位置,使得 B1Q⊥D1P;
(2)当 B1Q⊥D1P 时,求二面角 C1-PQ-A 的大小.
50. 如图,ABCD 是正方形,V 是平面 ABCD 外一点,且 VA=VB=VC=AB,求二面角 A-VB-C 的大小.