- 2021-06-16 发布 |
- 37.5 KB |
- 38页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习(文科数学)算法推理与证明课件(全国通用)
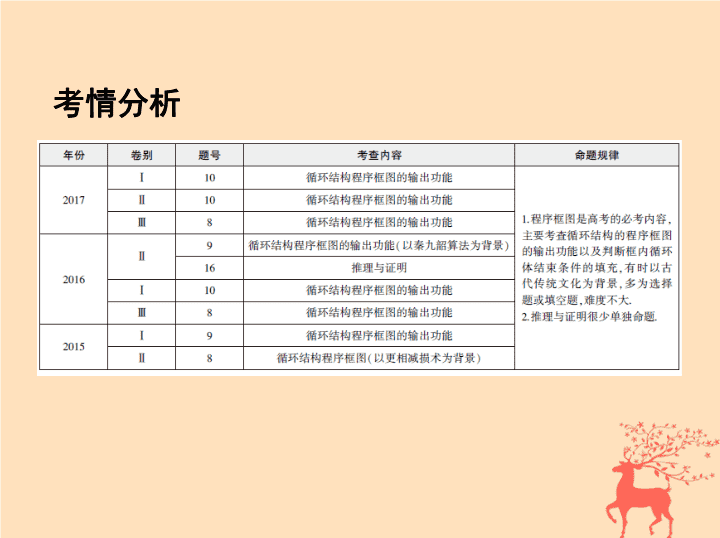
第4讲 算法、推理与证明 考情分析 总纲目录 考点一 算法(高频考点) 考点二 推理与证明 考点三 数学文化 考点一 算法(高频考点) 命题点 1.根据程序框图求解输出结果; 2.根据程序框图填写或选择判断框内的条件. 典型例题 (1)(2017课标全国Ⅱ,10,5分)执行下面的程序框图,如果输入的 a =-1, 则输出的 S = ( ) A.2 B.3 C.4 D.5 (2)(2017 课标全国 Ⅲ,8,5 分 ) 执行下面的程序框图 , 为使输出 S 的值小于 9 1, 则输入的正整数 N 的最小值为 ( ) A.5 B.4 C.3 D.2 (3)(2017 课标全国 Ⅰ,10,5 分 ) 下面程序框图是为了求出满足 3 n -2 n >1 000 的最小偶数 n , 那么在 和 两个空白框中 , 可以分别填入 ( ) A. A >1 000和 n = n +1 B. A >1 000和 n = n +2 C. A ≤ 1 000和 n = n +1 D. A ≤ 1 000和 n = n +2 答案 (1)B (2)D (3)D 解析 (1)由程序框图可得 S =0, a =-1, K =1 ≤ 6; S =0+(-1) × 1=-1, a =1, K =2 ≤ 6; S =-1+1 × 2=1, a =-1, K =3 ≤ 6; S =1+(-1) × 3=-2, a =1, K =4 ≤ 6; S =-2+1 × 4=2, a =-1, K =5 ≤ 6; S =2+(-1) × 5=-3, a =1, K =6 ≤ 6; S =-3+1 × 6=3, a =-1, K =7>6,退出循环,输出 S =3.故选B. (2)要求 N 的最小值,观察选项,发现其中最小的值为2,不妨将2代入检验. 当输入的 N 为2时,第一次循环, S =100, M =-10, t =2;第二次循环, S =90, M =1, t =3,此时退出循环,输出 S =90,符合题意,故选D. (3)本题求解的是满足3 n -2 n >1 000的最小偶数 n ,判断循环结构为当型循 环结构,即满足条件要执行循环体,不满足条件应输出结果,所以判断语 句应为 A ≤ 1 000,另外,所求为满足不等式的偶数解,因此 中语句应 为 n = n +2,故选D. 方法归纳 解答程序框图问题的三个关注点 (1)弄清程序框图的三种基本结构,按指向执行直至结束. (2)关注输出的是哪个量,何时结束. (3)解答循环结构问题时,要写出每一次的结果,防止运行程序不彻底,同 时注意区分计数变量与循环变量. 跟踪集训 1.(2017江西南昌十校联考)阅读如图所示的程序框图,运行相应的程序, 则输出 S 的值为 ( ) A.1 B.2 C.-1 D.-5 答案 D 由程序框图知, S = =3, n =2; S =3-4=-1, n =3; S =-1-4=-5, n =4,此 时满足输出条件.故输出 S 的值为-5,选D. 2.(2017湖南湘中名校联考)执行如图所示的程序框图,如果运行结果为 5040,那么判断框中应填入 ( ) A. k <6? B. k <7? C. k >6? D. k >7? 答案 D 第一次循环,得 S =2, k =3;第二次循环,得 S =6, k =4;第三次循 环,得 S =24, k =5;第四次循环,得 S =120, k =6;第五次循环,得 S =720, k =7;第六 次循环,得 S =5 040, k =8,此时满足题意,退出循环,输出的 S =5 040,故判断 框中应填入“ k >7?”,故选D. 考点二 推理与证明 1.归纳推理 (1)归纳推理是由某类事物的部分对象具有某些特征,推出该类事物的 全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推 理. (2)归纳推理的思维过程如下: 试验、观察→概括、推广→猜测一般性结论 2.类比推理 (1)类比推理是由两类对象具有某些类似特征和其中一类对象的某些已 知特征,推出另一类对象也具有这些特征的推理. (2)类比推理的思维过程如下: 观察、比较→联想、类推→猜测新的结论 典型例题 (1)(2017课标全国Ⅱ,9,5分)甲、乙、丙、丁四位同学一起去向老 师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在 给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家 说:我还是不知道我的成绩.根据以上信息,则 ( ) A.乙可以知道四人的成绩 B.丁可以知道四人的成绩 C.乙、丁可以知道对方的成绩 D.乙、丁可以知道自己的成绩 (2)(2017 河南郑州第三次质量预测 ) 中国有句名句“运筹帷幄之中 , 决胜 千里之外” . 其中的“筹”原意是指 《 孙子算经 》 中记载的算筹 , 古代 是用算筹来进行计算的,算筹是将几寸长的小竹棍摆在平面上进行运 算,算筹的摆放形式有纵、横两种形式,如下: 表示一个多位数时 , 像阿拉伯计数一样 , 把各个数位的数码从左到右排 列 , 但各位数码的筹式需要纵横相间 , 个位 , 百位 , 万位数用纵式表示 , 十 位 , 千位 , 十万位数用横式表示 , 以此类推 , 例如 6 613 用算筹表示就是 : , 则 5 288 用算筹可表示为 ( ) 答案 (1)D (2)C 解析 (1)由题意可知,“甲看乙、丙的成绩,不知道自己的成绩”说明 乙、丙两人是一个优秀一个良好,则乙看了丙的成绩,可以知道自己的 成绩,丁看了甲的成绩,也可以知道自己的成绩.故选D. (2)个位,百位数用纵式表示,十位,千位数用横式表示,所以5 288可表示 为 ,故选C. 方法归纳 合情推理的解题思路 (1)在进行归纳推理时,要先根据已知的部分个体,把它们适当变形,找出 它们之间的联系,从而归纳出一般结论. (2)在进行类比推理时,要充分考虑已知对象性质的推理过程,然后通过 类比,推导出类比对象的性质. (3)归纳推理的关键是找规律,类比推理的关键是看共性. 跟踪集训 1.观察下列等式: 1+2+3+ … + n = n ( n +1); 1+3+6+ … + n ( n +1)= n ( n +1)( n +2); 1+4+10+ … + n ( n +1)( n +2)= n ( n +1)( n +2)( n +3); 可以推测1+5+15+ … + n ( n +1)( n +2)( n +3)= . 解析 根据式子中的规律可知,等式右侧为 n ·( n +1)( n +2)( n + 3)( n +4)= n ( n +1)( n +2)( n +3)( n +4). 答案 n ( n +1)( n +2)( n +3)( n +4) 2.(2017北京,14,5分)某学习小组由学生和教师组成,人员构成同时满足 以下三个条件: (i)男学生人数多于女学生人数; (ii)女学生人数多于教师人数; (iii)教师人数的两倍多于男学生人数. ①若教师人数为4,则女学生人数的最大值为 ; ②该小组人数的最小值为 . 答案 ①6 ②12 解析 设男学生人数为 x ,女学生人数为 y ,教师人数为 z ,由已知得 且 x , y , z 均为正整数. ①当 z =4时,8> x > y >4,∴ x 的最大值为7, y 的最大值为6, 故女学生人数的最大值为6. ② x > y > z > ,当 x =3时,条件不成立,当 x =4时,条件不成立,当 x =5时,5> y > z > ,此时 z =3, y =4. ∴该小组人数的最小值为12. 考点三 数学文化 典型例题 (1)(2016课标全国Ⅱ,9,5分)中国古代有计算多项式值的秦九韶算 法,下图是实现该算法的程序框图.执行该程序框图,若输入的 x =2, n =2, 依次输入的 a 为2,2,5,则输出的 s = ( ) A.7 B.12 C.17 D.34 (2)(2015课标Ⅱ,8,5分)下边程序框图的算法思路源于我国古代数学名 著《九章算术》中的“更相减损术”.执行该程序框图,若输入的 a , b 分 别为14,18,则输出的 a = ( ) A.0 B.2 C.4 D.14 答案 (1)C (2)B 解析 (1)执行程序框图,输入 a 为2时, s =0 × 2+2=2, k =1,此时 k >2不成立;再 输入 a 为2时, s =2 × 2+2=6, k =2,此时 k >2不成立;再输入 a 为5时, s =6 × 2+5= 17, k =3,此时 k >2成立,结束循环,输出 s 为17,故选C. (2)执行程序框图:当 a =14, b =18时, a < b ,则 b =18-14=4;当 a =14, b =4时, a > b , 则 a =14-4=10;当 a =10, b =4时, a > b ,则 a =10-4=6;当 a =6, b =4时, a > b ,则 a =6-4 =2;当 a =2, b =4时, a < b ,则 b =4-2=2,此时 a = b =2,输出 a =2,故选B. 方法归纳 解决此类问题要充分理解题意,弄清输出条件. 跟踪集训 1.(2017湖北七市(州)联考)秦九韶是我国南宋时期的数学家,他在所著 的《数书九章》中提出的秦九韶算法,至今仍是比较先进的算法.如图 所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输 入 n , x 的值分别为3,4,则输出 v 的值为 ( ) A.6 B.25 C.100 D.400 答案 C 输入 n =3, x =4, v =1, i =3-1=2; v =1 × 4+2=6, i =2-1=1; v =6 × 4+1=25, i =1-1=0; v =25 × 4=100, i =0-1=-1<0.程序结束,输出的 v =100.故选C. 2.(2017四川成都第一次诊断性检测)我国南北朝时期的数学家祖暅提 出体积的计算原理(祖暅原理):“幂势既同,则积不容异”.“势”即是 高,“幂”是面积.意思是如果两等高的几何体在同高处截得两几何体 的截面积相等,那么这两个几何体的体积相等.类比祖暅原理,如图所示, 在平面直角坐标系中, ABCD 是一个不规则的封闭图形, EFGH 是一个上 底为1的梯形,且当实数 t 取[0,3]上的任意值时,直线 y = t 被 ABCD 和 EFGH 所截得的两线段长始终相等,则 ABCD 的面积为 . 答案 解析 依题意,类比可知 ABCD 的面积等于梯形 EFGH 的面积,为 × 3 = . 1.(2017北京,3,5分)执行如图所示的程序框图,输出的 s 值为 ( ) A.2 B. C. D. 随堂检测 答案 C 由程序框图可知 k =1, s =2; k =2, s = ; k =3, s = . 此时 k <3不成立, 故输出 s = .故选C. 2.(2017山东,6,5分)执行下面的程序框图,当输入的 x 的值为4时,输出的 y 的值为2,则空白判断框中的条件可能为 ( ) A. x >3 B. x >4 C. x ≤ 4 D. x ≤ 5 答案 B ∵log 2 4=2,4+2=6,∴当 x =4时,应执行否. 结合选项知选B. 3.(2017安徽合肥模拟)如图所示的程序框图的算法思想源于数学名著 《几何原本》中的“辗转相除法”,执行该程序框图(图中“ m MOD n ”表示 m 除以 n 的余数),若输入的 m , n 分别495,135,则输出的 m = ( ) A.0 B.5 C.45 D.90 答案 C 该程序框图是求495与135的最大公约数,由495=135 × 3+90, 135=90 × 1+45,90=45 × 2,所以495与135的最大公约数是45,所以输出的 m =45,故选C. 4.设△ ABC 的三边长分别为 a , b , c ,△ ABC 的面积为 S ,则△ ABC 的内切圆 半径为 r = .将此结论类比到空间四面体:设四面体 S - ABC 的四个 面的面积分别为 S 1 , S 2 , S 3 , S 4 ,体积为 V ,则四面体的内切球半径为 ( ) A. B. C. D. 答案 C 设四面体的内切球的球心为 O ,球心 O 到四个面的距离都是 R ,则有 V = ( S 1 + S 2 + S 3 + S 4 ) R ,所以 R = .查看更多