- 2021-06-16 发布 |
- 37.5 KB |
- 43页


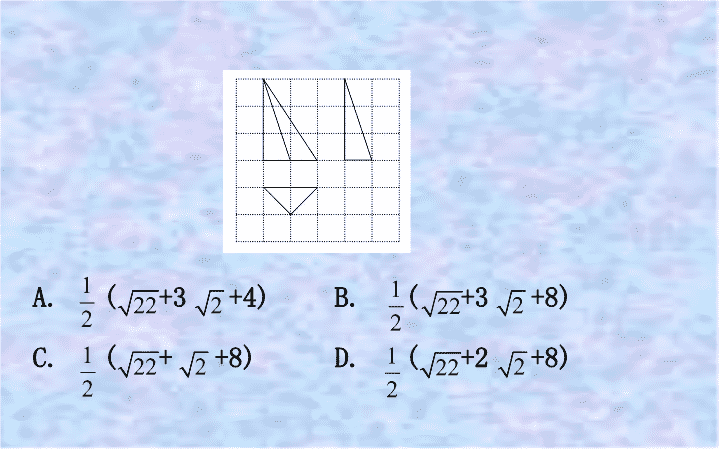
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届高考理科数学二轮专题复习课件:专题4 立体几何2-4-高考小题 1
第 1 课时 空间几何体的表面积与体积计算 考向一 空间几何体的三视图与直观图 ( 保分题型考点 ) 【题组通关】 1. 如图 , 网格纸中的小正方形的边长均为 1, 图中粗线画出的是一个几何体的三视图 , 则这个几何体的表面积为 ( ) A. ( +3 +4) B. ( +3 +8) C. ( + +8) D. ( +2 +8) 【解析】 选 B. 根据三视图可知该几何体是底面为直角 三角形的三棱锥 , 其表面积 S= 2. 某三棱锥的三视图如图所示 , 其侧视图为直角三角形 , 则该三棱锥最长的棱长等于 ( ) A.4 B. C. D.5 【解析】 选 C. 根据几何体的三视图 , 知该几何体是底面 为直角三角形 , 两侧面垂直于底面 , 高为 5 的三棱锥 P-ABC( 如图所示 ). 棱锥最长的棱长 PA= 3. 如图 , 在底面边长为 1, 高为 2 的正四棱柱 ABCD-A 1 B 1 C 1 D 1 中 , 点 P 是平面 A 1 B 1 C 1 D 1 内一点 , 则三棱锥 P-BCD 的正视图与侧视图的面积之和为 世纪金榜导学号 ( ) A.1 B.2 C.3 D.4 【解析】 选 B. 设点 P 在平面 A 1 ADD 1 的射影为 P′, 在平面 C 1 CDD 1 的射影为 P″, 如图所示 . 所以三棱锥 P-BCD 的正视图与侧 视图分别为 △P′AD 与 △P″CD, 因此所求面积 S=S △P′AD +S △P″CD = ×1×2+ ×1×2=2. 4. 将一个长方体沿相邻三个面的对角线截去一个棱锥 , 得到的几何体的正视图与俯视图如图所示 , 则该几何体的侧视图为 ( ) 世纪金榜导学号 【解析】 选 B. 由几何体的正视图和俯视图可知该几何体的直观图为长方体截去了右上方的一个角如图 ①, 故其侧视图为图 ②. 【拓展提升】 由三视图还原到直观图的思路 (1) 根据俯视图确定几何体的底面 . (2) 根据正视图或侧视图确定几何体的侧棱与侧面的特征 , 调整实线和虚线所对应的棱、面的位置 . (3) 确定几何体的直观图形状 . 考向二 几何体的表面积与体积 ( 保分题型考点 ) 【题组通关】 1. 如图为一个多面体的三视图 , 则该多面体的体积为 ( ) A. B.7 C. D. 【解析】 选 B. 由三视图知 , 该几何体是 棱长为 2 的正方体截去三棱锥 D-D 1 MN 与 三棱锥 A-MA 1 B 后剩下的多面体 所以该几何体的体积 V=2 3 - ×1 2 ×2- ×2×1×2=7. 2. 如图是某几何体的三视图 , 则该几何体的体积为 ( ) A.π+ B.2π+ C.π+ D.2π+ 【解析】 选 C. 由三视图可知 : 该几何体是由上下两部分 组成 , 上面是两个全等的三棱锥 , 下面是一个圆柱体 ; 所以该几何体的体积为 :V=π×1 2 ×1+2× ×2×1×1=π+ . 3.(2019· 北京高考 ) 某几何体是由一个正方体去掉一个四棱柱所得 , 其三视图如图所示 . 如果网格纸上小正方形的边长为 1, 那么该几何体的体积为 ________. 【解析】 由三视图可知 , 正方体体积 V 1 =4 3 =64, 四棱柱 体积 V 2 = ×4=24, 所以该几何体体积 V=V 1 -V 2 =40. 答案 : 40 4. 已知一个几何体的三视图如图所示 ( 单位 :cm), 则该几何体的体积为 ________cm 3 . 世纪金榜导学号 【解析】 根据三视图可知几何体下部是一个 高为 1, 底面半径为 1 的圆锥 . 上部是一个高为 3 的圆柱被一个斜平面所截后的一部分 , 底面 半径是 1, 所以几何体的体积是 ×1 2 ×π×1+π×1 2 ×(1+ ×2)= . 答案 : 5. 如图 , 某三棱锥的三视图是三个边长相等的正方形及 对角线 , 若该三棱锥的体积是 , 则它的棱长是 ________, 它的表面积是 ________. 世纪金榜导学号 【解析】 由题设及几何体的三视图知 , 该几何体是一个正方体截 去 4 个三棱锥后剩余的内接正三棱锥 B-A 1 C 1 D( 如图所示 ). 设正方体的棱长为 a, 则几何体的体积是 V=a 3 -4× × a 2 ·a= a 3 = , 所以 a=1, 所以三棱锥的棱长为 , 因此 , 该三棱锥的表面积为 S=4× ×( ) 2 =2 . 答案 : 2 【拓展提升】 1. 由几何体的三视图求其表面积 : (1) 关键是分析三视图确定几何体中各元素之间的位置关系及度量大小 . (2) 还原几何体的直观图 , 套用相应的面积公式 . 2. 求三棱锥的体积 : 等体积转化是常用的方法 , 转换原则是其高易求 , 底面放在已知几何体的某一面上 . 3. 求不规则几何体的体积 常用分割或补形的思想 , 将不规则几何体转化为规则几何体以易于求解 . 【补偿训练】 (2017· 北京高考 ) 某三棱锥的三视图如图所示 , 则该三棱锥的体积为 ( ) A.60 B.30 C.20 D.10 【解析】 选 D. 由三棱锥的三视图可知 , 该三棱锥的直观 图为三棱锥 A-BCD, 如图所示 , 其所在长方体的长、宽、高 分别为 5,3,4, 所以 V A-BCD = × ×5×3×4=10. 考向三 多面体与球的切、接问题 ( 压轴题型考点 ) 【典例】 1.(2016· 全国卷 Ⅲ) 在封闭的直三棱柱 ABC - A 1 B 1 C 1 内有一个体积为 V 的球 . 若 AB⊥BC,AB=6, BC=8, ① AA 1 =3, 则 V 的最大值 ② 是 ( ) A.4π B. C.6π D. 【解析】 选 B. 当球的半径最大时 , 球的体积最大 . 在直 三棱柱内 , 当球和三个侧面都相切时 , 因为 AB⊥BC,AB=6, BC=8, 所以 AC=10, 底面的内切圆的半径即为此时球的半 径 r= =2, 直径为 4> 侧棱 . 所以球的最大直径 为 3, 半径为 , 此时体积 V= . 2.(2019· 太原三模 ) 已知正方形 ABCD 的边长为 2,CD 边 的中点为 E, 现将 △ADE,△BCE 分别 沿 AE,BE 折起 , 使得 C 、 D 两点重合为一点记为 P ③ , 则 四面体 P-ABE 外接球 ④ 的表面积是 世纪金榜导学号 ( ) A. B. C. D. 【解析】 选 C. 如图 ,PE⊥PA,PE⊥PB,PE=1,△PAB 是边长 为 2 的等边三角形 , 设 H 是 △PAB 的中心 ,OH⊥ 平面 PAB,O 是外接球的球心 , 则 OH= PE= ,PH= , 则 R 2 =OP 2 =OH 2 +PH 2 = . 故四面体 P-ABE 外接球的表面积为 4πR 2 = . 【题眼直击】 题目 题眼 思维导引 1. ① 利用勾股定理求 AC 的长 ② 求球的半径的最大值 2. ③ 确定几何体中不变的元素 ④ 确定外接球的球心 【拓展提升】 空间几何体与球接、切问题的求解方法 (1) 确定球心的位置 , 弄清球的半径 ( 直径 ) 与几何体的位置和数量关系 . (2) 求解球与棱柱、棱锥的接、切问题时 , 一般过球心及接、切点作截面 , 把空间问题转化为平面图形与圆的接、切问题 , 再利用平面几何知识寻找几何中元素间的关系求解 . (3) 补成正方体、长方体、正四面体、正棱柱、圆柱等规则几何体 . 【变式训练】 已知直三棱柱 ABC-A 1 B 1 C 1 的 6 个顶点都在球 O 的球面上 , 若 AB=3,AC=4,AB⊥AC,AA 1 =12, 则球 O 的表面积为 ____. 【解析】 将直三棱柱补形为长方体 ABEC-A 1 B 1 E 1 C 1 , 则球 O 是长方体 ABEC-A 1 B 1 E 1 C 1 的外接球 . 所以体对角线 BC 1 的 长为球 O 的直径 . 因此 2R= =13. 故 S 球 =4πR 2 =169π. 答案 : 169π查看更多