- 2021-06-16 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
云南省曲靖市宣威市民族中学2019-2020学年高二下学期第一次月考数学(文)试卷
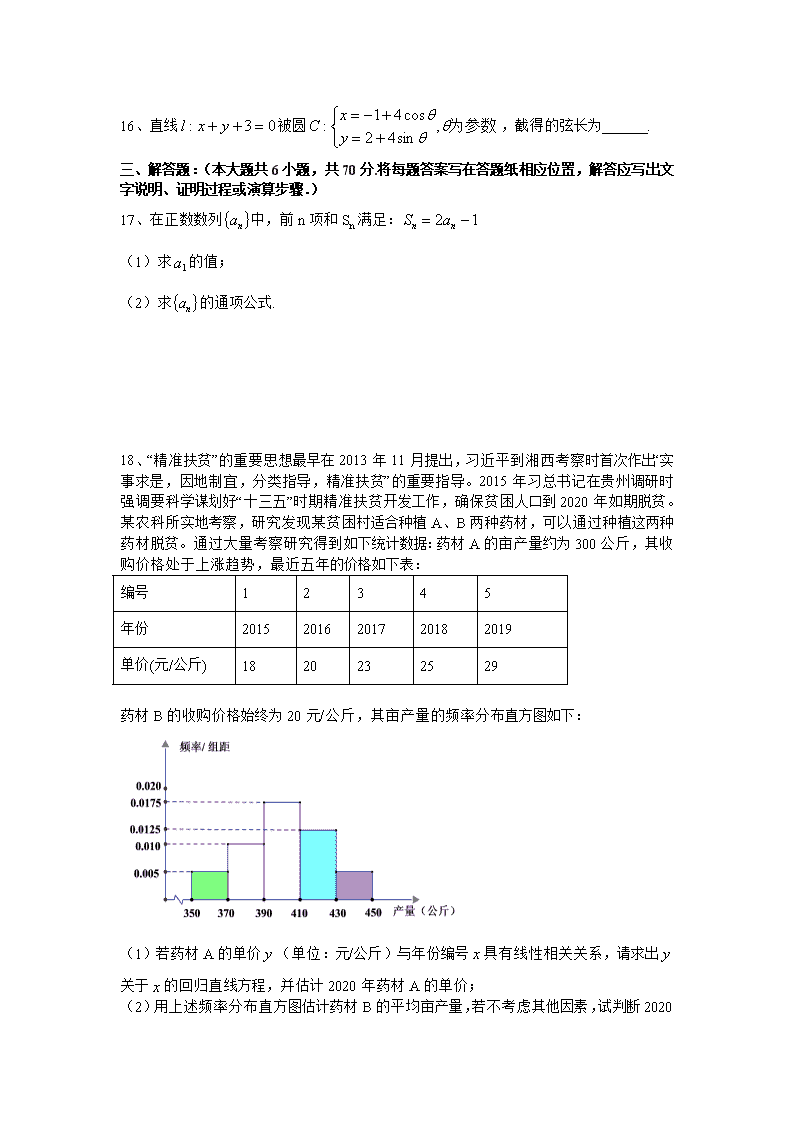
云南省曲靖市宣威市民族中学2019-2020学年高二下学期第一次月考数学(文)试卷 (本试卷共150分 考试时间120分钟) 第I卷 (选择题 共60分) 一. 选择题(每题只有一个答案是正确的,每小题5分,共60分) 1、若,则( ) A. B. C. D. 2、已知i是虚数单位,若复数z满足,则=( ) A.-2i B.2i C.-2 D.2 3、“”是“”的( ) A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既不充分也不必要条件 4、一个频数分布表(样本容量为30)不小心被损块了一部分,只记得样本中数据在上的频率为0.8,则估计样本内的数据个数为( ) 分组 频数 A. B. C. D. 5、为了得到函数的图象,只需将函数y=cos2x的图象( ) A.向左平移个单位长度 B.向右平移个单位长度 C.向左平移个单位长度 D.向右平移个单位长度 6、下列说法错误的是( ) A.若命题,使得,则,都有 B.命题“若,则”的逆否命题为假命题 C.命题“若,则”的否命题是:“若,则” D.已知,使得,,都有,则“ ”为假命题 7、已知,并且成等差数列,则的最小值为( ) A.2 B.4 C.5 D.9 8、己知某产品的销售额与广告费用之间的关系如下表: (单位:万元) 0 1 2 3 4 (单位:万元) 10 15 20 30 35 若求得其线性回归方程为,则预计当广告费用为6万元时的销售额为( ) A.42万元 B.45万元 C.48万元 D.51万元 9、点的直角坐标是,则它的极坐标是( ) A. B. C. D. 10、在极坐标系中,与点关于极点对称的点的坐标是 ( ) A. B. C. D. 11、已知,是虚数单位,是的共轭复数,下列说法与“为纯虚数”不等价的是( ) A. B.或,且 C. D. 12、已知,分别是双曲线的左、右焦点,是右顶点,过且垂直于轴的直线与双曲线交于,两点,若是直角三角形,则该双曲线离心率的值是 ( ) A. B. C. 2 D. 3 第Ⅱ卷 (非选择题 共90分) 二、填空题(本题共4小题,每小题5分,共20分) 13、设集合,若,则实数______. 14、若椭圆的一个焦点与抛物线的焦点重合,则______. 15、在区间上随机选取一个实数,则事件发生的概率为_____. 16、直线被圆,截得的弦长为______. 三、解答题:(本大题共6小题,共70分.将每题答案写在答题纸相应位置,解答应写出文字说明、证明过程或演算步骤.) 17、在正数数列中,前n项和Sn满足: (1)求的值; (2)求的通项公式. 18、“精准扶贫”的重要思想最早在2013年11月提出,习近平到湘西考察时首次作出“实事求是,因地制宜,分类指导,精准扶贫”的重要指导。2015年习总书记在贵州调研时强调要科学谋划好“十三五”时期精准扶贫开发工作,确保贫困人口到2020年如期脱贫。某农科所实地考察,研究发现某贫困村适合种植A、B两种药材,可以通过种植这两种药材脱贫。通过大量考察研究得到如下统计数据:药材A的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表: 编号 1 2 3 4 5 年份 2015 2016 2017 2018 2019 单价(元/公斤) 18 20 23 25 29 药材B的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下: (1)若药材A的单价(单位:元/公斤)与年份编号具有线性相关关系,请求出关于的回归直线方程,并估计2020年药材A的单价; (2)用上述频率分布直方图估计药材B的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材A还是药材B?并说明理由. 附:. 19、三角形中,角所对边分别为,且. (1)若,求的值; (2)若,求三角形的面积. 20、2022年北京冬奥运动会即第24届冬季奥林匹克运动会将在2022年2月4日至2月20日在北京和张家口举行,某研究机构为了了解大学生对冰壶运动的兴趣,随机从某大学生中抽取了100人进行调查,经统计男生与女生的人数比为,男生中有20人表示对冰壶运动有兴趣,女生中有15人对冰壶运动没有兴趣. 有兴趣 没有兴趣 合计 男 20 女 15 合计 100 (1)完成列联表,并判断能否有把握认为“对冰壶运动是否有兴趣与性别有关”? (2)用分层抽样的方法从样本中对冰壶运动有兴趣的学生中抽取6人,求抽取的男生和女生分别为多少人?若从这6人中选取两人作为冰壶运动的宣传员,求选取的2人中恰好有1位男生和1位女生的概率. 附:,其中 0.150 0.100 0.050 0.025 0.010 2.072 2.076 3.841 5.024 6.635 21、已知函数. (1)若函数的图象在处的切线方程为,求的值; (2)若函数在上是增函数,求实数的最大值. 22、已知曲线的极坐标方程为,曲线的极坐标方程为(, 曲线、相交于点A,B. (1)将曲线、的极坐标方程化为直角坐标方程; (2)求弦的长. 参考答案 一、单项选择 1、【答案】C 2、【答案】A 3、【答案】B 4、【答案】B 5、【答案】B 6、【答案】D 7、【答案】D 8、【答案】C 9、【答案】A 10、【答案】D 11、【答案】D 12、【答案】C 二、填空题 13、【答案】 14、【答案】 15、【答案】 16、【答案】 三、解答题 17、【答案】(1)1(2) 试题分析:(1)当时,; (2)当时,,即用公式法求解通项公式 【详解】 (1)当时,, (2)当时,,即 是首项为1,公比为2的等比数列, 18、 19、【答案】(1);(2). 试题分析:(1)根据a2+c2=b2+ac.由余弦定理求出cosB,cosA,再求解sinA,sinB,根据sinC=sin(B+A)打开即可求解.(2)由a2+c2=b2+ac.b,a=3c,根据余弦定理求解a,c的值,即可求出三角形ABC的面积. 【详解】 (1)由余弦定理,cosB.又B为三角形内角,则B=. 因为cosA=,且A为三角形内角,则sinA=, 故sinC=sin(B+A)=sin(+A)=cosA+sinA=. (2)由a=3c,由余弦定理知:b2=a2+c2-2accosB,则7=9c2+c2-3c2,解得c=1,则a=3.面积S=acsinB=. 【点睛】 本题考查了余弦定理的运用和三角形ABC的面积的计算.属于基础题. 20、【答案】(1)填表见解析,有把握认为“对冰壶运动是否有兴趣与性别有关”(2)抽取的男生数、女生数分别为:2,4,选取的2人中恰好有1位男生和1位女生的概率为 试题分析:(1)先得2×2列联表,在根据表中数据计算,结合临界值表可得到结论; (2)对冰壶运动有兴趣的学生共有60人,从中抽取6人,抽取的男生数,女生数分别为:,.再用列举法得到从6中选取2人的基本事件和恰好有1位男生和1位女生的基本事件,用古典概型概率公式可得. 【详解】 (1)根据题意得如下列联表: 有兴趣 没有兴趣 合计 男 20 25 45 女 40 15 55 合计 60 40 100 所以 所以有把握认为“对冰壶运动是否有兴趣与性别有关”, (2)对冰壶运动有兴趣的学生共60人,从中抽取6人,抽取的男生数、女生数分别为: ,. 记2名男生为,;女生为,,,,则从中选取2人的基本事件 为:,,,,,,,,,,,,,,共15个, 其中含有1男1女的基本事件为:,,,,,,,共8个 记“对冰壶运动有兴趣的学生中抽取6人做宣传员,恰好一男一女”的事件为,则, 所以选取的2人中恰好有1位男生和1位女生的概率为. 【点睛】 本题考查了独立性检验,属中档题. 21、【答案】(1);(2)的最大值为 22、【答案】(1)y=x, x2+y2=6x (2) 圆心到直线的距离d=, r=3, 弦长AB=3查看更多