2019届 二轮 选修4 专题卷

2019届 二轮 选修4 专题卷

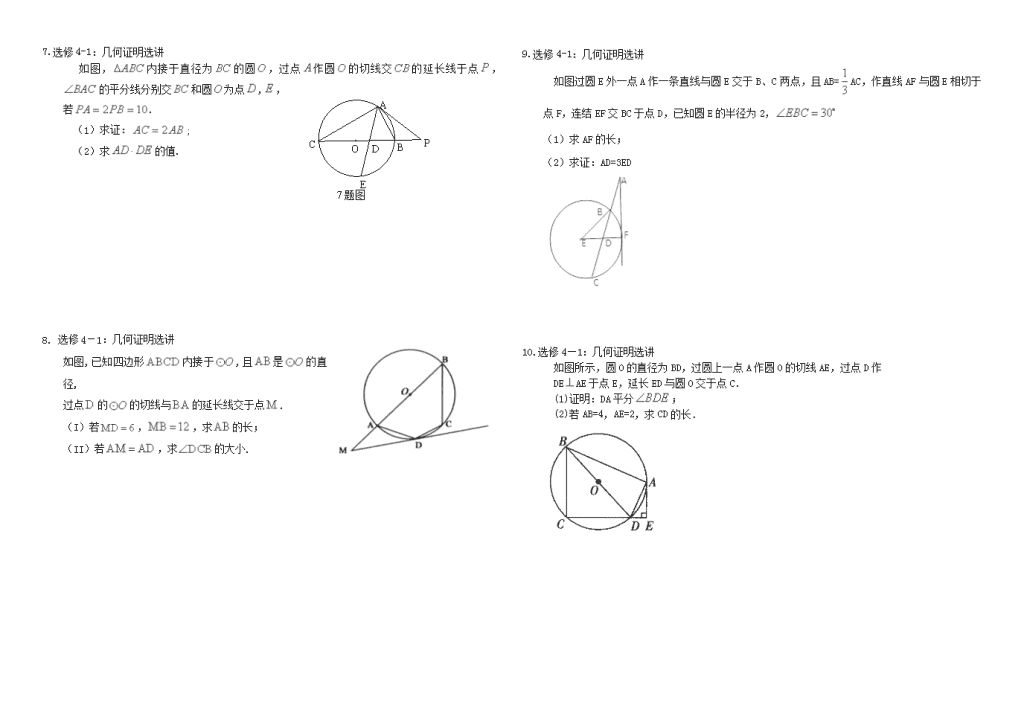
选修作业专练 姓名：__________班级：__________考号：__________‎ 一 ‎、选做解答题（本大题共10小题，共100分）‎ 选修4-5：不等式选讲 已知函数 ‎（1）求函数的值域 ‎（2）求不等式:的解集．‎ 选修45：不等式选讲 已知函数,,．‎ ‎（I）当时,解不等式: ； ‎ ‎（II）若且,证明：，并说明等号成立时满足的条件。‎ 选修4-4：坐标系与参数方程 已知极坐标系的极点在直角坐标系的原点处，极轴与轴非负半轴重合．直线的参数方程为：（为参数），曲线的极坐标方程为：．‎ ‎（1）写出曲线的直角坐标方程，并指明是什么曲线；‎ ‎（2）设直线与曲线相交于两点，求的值．‎ 选修4-4：坐标系与参数方程 已知曲线： （为参数），：（为参数）．‎ ‎（1）化，的方程为普通方程，并说明它们分别表示什么曲线；‎ ‎（2）若上的点对应的参数为，为上的动点，求中点到直线（为参数）距离的最小值．‎ 选修4—4：坐标系与参数方程选讲 已知直线：（为参数，a为的倾斜角），以坐标原点为极点,轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.‎ ‎（1）若直线与曲线相切，求的值；‎ ‎（2）设曲线上任意一点的直角坐标为，求的取值范围.‎ 选修44：坐标系与参数方程 已知椭圆C的极坐标方程为，‎ 点为其左，右焦点，直线的参数方程为( )．‎ ‎（I）求直线和曲线C的普通方程；（II）求点到直线的距离之和. ‎ 选修4-1：几何证明选讲 P A B C D E ‎7题图 O ‎ 如图，内接于直径为的圆，过点作圆的切线交的延长线于点，的平分线分别交和圆为点,，‎ 若.‎ ‎ （1）求证：;‎ ‎ （2）求的值.‎ 选修4－1：几何证明选讲 如图,已知四边形内接于,且是的直径,‎ 过点的的切线与的延长线交于点.‎ ‎（I）若，，求的长；‎ ‎（II）若，求的大小.‎ 选修4-1：几何证明选讲 ‎ 如图过圆E外一点A作一条直线与圆E交于B、C两点，且AB=AC，作直线AF与圆E相切于点F，连结EF交BC于点D，已知圆E的半径为2，‎ ‎（1） 求AF的长；‎ ‎（2） 求证：AD=3ED 选修4—1：几何证明选讲 ‎ 如图所示，圆0的直径为BD，过圆上一点A作圆O的切线AE，过点D作 ‎ DEAE于点E，延长ED与圆0交于点C．‎ ‎ (1)证明：DA平分；‎ ‎ (2)若AB=4，AE=2，求CD的长．‎ 答案解析 一 ‎、选做解答题 【答案】 （1）[-3,3] ；（2）‎ ‎ 解析：（1）因为 ‎ 当2＜x＜5时，-3＜f(x) ＜3，所以，即函数值域为[-3,3]. ‎ ‎（2）由（1）可知， 当的解集为空集；‎ ‎ 当时，的解集为：；‎ 当时，的解集为：；‎ 综上，不等式的解集为：； ‎ ‎【思路点拨】一般遇到绝对值函数，通常先改写成分段函数，再结合各段对应的关系式进行解答.‎ 解: (Ⅰ)因为,所以原不等式为.‎ 当时, 原不等式化简为,即； ‎ 当时, 原不等式化简为,即无解；‎ 当时, 原不等式化简为,即. ‎ 综上,原不等式的解集为.‎ ‎（Ⅱ）由题知 , ，‎ 所以, 又等号成立当且仅当与同号或它们至少有一个为零. ‎ 【答案】(1) ，是以(2,0)为圆心，2为半径的圆；‎ ‎(2) 解析：(1)由得，得，即，所以曲线C是以(2,0)为圆心，2为半径的圆.‎ ‎（2）把代入，整理得， ‎ 设其两根分别为则，所以.‎ ‎【思路点拨】一般遇到直线上的点与直线经过的定点之间的距离关系问题时，可考虑利用直线参数方程中的参数的几何意义进行解答.‎ 【答案】（1），为圆心是(-4,3)，半径是1的圆，为中心是坐标原点，焦点在x轴上，长半轴长是8，短半轴长是3的椭圆；‎ ‎（2）． 解析：：（1）对两个参数方程消参得，为圆心是(-4,3)，半径是1的圆，为中心是坐标原点，焦点在x轴上，长半轴长是8，短半轴长是3的椭圆；（2）当时，，故 ，为直线x－2y－7=0，M到的距离，从而当时，d取得最小值.‎ ‎【思路点拨】当遇到由曲线的参数方程解答问题不方便时，可化成普通方程进行解答.‎ 解：（1）曲线C的直角坐标方程为 即 曲线C为圆心为(3,0)，半径为2的圆. ‎ ‎ 直线l的方程为: ‎ ‎∵直线l与曲线C相切 ∴ ‎ 即 ∵ aÎ[0,π) ∴a= ‎ ‎(法二)①将化成直角坐标方程为……2分 由消去得 ‎ ‎∵ 与C相切 ∴ Δ=64-48=0 解得cosa=∵ aÎ[0,π) ∴a= ‎ ‎（2）设 则 = ‎ ‎∴ 的取值范围是. ‎ 解：(Ⅰ) 直线普通方程为 ；曲线的普通方程为． ‎ ‎(Ⅱ) ∵,，∴点到直线的距离 ‎ 点到直线的距离 ∴ ‎ 解：（1）∵PA是圆O的切线 ∴ 又是公共角 ‎ ∴∽ ∴ ∴ ‎ ‎（2）由切割线定理得： ∴又PB=5 ∴ ‎ ‎ 又∵AD是的平分线 ∴∴ ∴ ‎ ‎ 又由相交弦定理得： ‎ 解：(Ⅰ)因为MD为的切线,由切割线定理知,‎ MD2=MAMB，又MD=6，MB=12，MB=MA+AB , 所以MA=3，AB==9. ‎ ‎（Ⅱ）因为AM=AD，所以∠AMD=∠ADM,‎ 连接DB，又MD为的切线,由弦切角定理知,∠ADM=∠ABD， ‎ 又因为AB是的直径,所以∠ADB为直角，‎ 即∠BAD=90°-∠ABD. 又∠BAD=∠AMD+∠ADM=2∠ABD,‎ 于是90°-∠ABD=2∠ABD,所以∠ABD=30°,所以∠BAD=60°. ‎ 又四边形ABCD是圆内接四边形,所以∠BAD+∠DCB=180°,所以∠DCB=120° ‎ 【答案】（1）AF=3；（2）证明：见解析.‎ 解析：（1）延长BE交圆E于点M，连接CM，则∠BCM=90°，‎ 又BM=2BE=4，∠EBC=30°，所以BC=，根据切割线定理得:‎ ‎，所以AF=3‎ ‎(2)过E作EH⊥BC与H，则△EDH∽△ADF ,‎ 从而有,又由题意知BH= ‎ 所以EH=1，因此，即AD=3ED ‎ ‎【思路点拨】（1）根据切割线定理知，只需求出线段BC的长，为此延长BE交圆E于点M，连接CM，在Rt△BCM中求得BC=，从而得AF=3；（2）取BC中点H连接EH，‎ 由△EDH∽△ADF可证得结论.‎ 【答案】（1）略（2）‎ ‎【解析】（1）证明：∵AE是⊙O的切线，∴∠DAE=∠ABD， ∵BD是⊙O的直径，∴∠BAD=90°，∴∠ABD+∠ADB=90°， 又∠ADE+∠DAE=90°，∴∠ADB=∠ADE．∴DA平分∠BDE． （2）由（1）可得：△ADE∽△BDA，∴， ∴，化为BD=2AD．∴∠ABD=30°．∴∠DAE=30°．∴DE=AEtan30°=． 由切割线定理可得：AE2=DE•CE，∴22=(+CD)，解得CD=．‎ ‎【思路点拨】（1）由于AE是⊙O的切线，可得∠DAE=∠ABD．由于BD是⊙O的直径，可得∠BAD=90°，因此∠ABD+∠ADB=90°，∠ADE+∠DAE=90°，即可得出∠ADB=∠ADE．． （2）由（1）可得：△ADE∽△BDA，可得 ，BD=2AD．因此∠ABD=30°．利用DE=AEtan30°．切割线定理可得：AE2=DE•CE，即可解出．‎