上海教育高中数学三上平面及其基本性质一

上海教育高中数学三上平面及其基本性质一

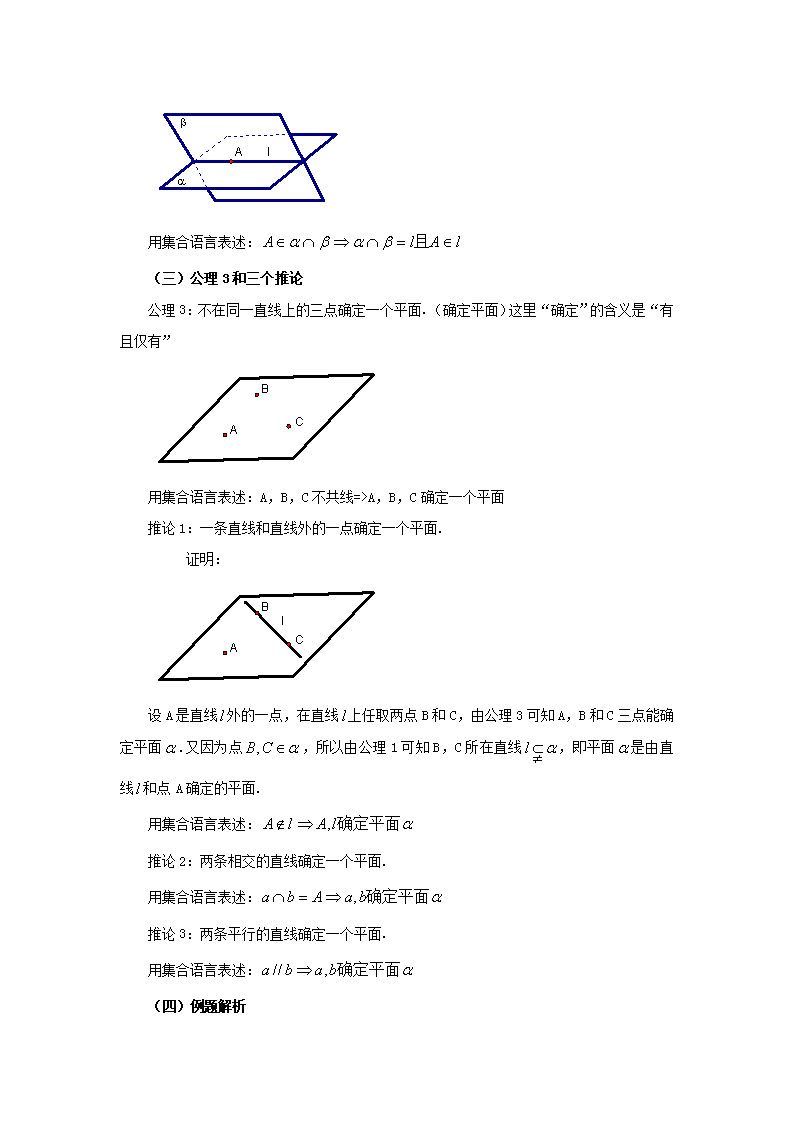
高考资源网14．1 （2）平面及其基本性质 ‎ ——三个公理三个推论 ‎　一、教学内容分析 本节的重点和难点是三个公理三个推论.三个公理和三个推论是立体几何的基础，公理1确定直线在平面上；公理2明确两平面相交于一直线；公理3及三个推论给出了确定平面的条件.这些是后面学习空间直线与平面位置关系的基础.所以让学生透彻理解这些公理和性质，把现实中的具体空间高考资源网问题抽象出来，初步认识直线与平面、平面与平面之间的关系并体会立体几何的基本思想，从而培养学生的空间想象能力，有利于学生更快更好的学习立体几何.‎ 二、教学目标设计 理解平面的基本性质，能用三个公理三个推论解决简单的空间线面问题；了解一些简单的证明.培养空间想象能力，提高学习数学的自觉性和兴趣.‎ 三、教学重点及难点 三个公理，三个推论.‎ 四、教学过程设计 ‎ 一、讲授新课 ‎（一）公理1‎ 如果直线上有两个点在平面上，那么直线在平面上.‎ ‎（直线在平面上）‎ 用集合语言表述：‎ ‎（二）公理2‎ 如果不同的两个平面、有一个公共点A，那么、的交集是过点A的直线.（平面与平面相交）‎ 用集合语言表述：‎ ‎（三）公理3和三个推论 公理3：不在同一直线上的三点确定一个平面.（确定平面）这里“确定”的含义是“有且仅有”‎ 用集合语言表述：A，B，C不共线=>A，B，C确定一个平面 推论1：一条直线和直线外的一点确定一个平面.‎ 高·考￥资%源~网证明：‎ 设A是直线外的一点，在直线上任取两点B和C，由公理3可知A，B和C三点能确定平面.又因为点，所以由公理1可知B，C所在直线，即平面是由直线和点 A确定的平面.‎ 用集合语言表述：‎ 推论2：两条相交的直线确定一个平面.‎ 用集合语言表述：‎ 推论3：两条平行的直线确定一个平面.‎ 用集合语言表述：‎ ‎（四）例题解析 例1如图，正方体中，E，F分别是的中点，问：直线EF和BC是否相交？ ‎ 如果相交，交点在那个平面内？ ‎ 解：‎ 又，则直线EF和BC共面；‎ 设直线EF和BC相交于点p，则p在直线BC上，即点P在平面ABCD上.‎ ‎[说明]利用公理1确定直线在平面内.‎ 例2 如图，若，求证：直线C必过点P.‎ 解：‎ ‎ [结论]三个平面两两相交得到三条交线，若其中两条交于一点，另一条必过此公共点.‎ 例3 空间三个点能确定几个平面？‎ 空间四个点能确定几个平面？‎ 解：三点共线有无数多个平面；三点不共线可以确定一个平面.所以三点可以确定一个或无数个平面.‎ 四点共线有无数个平面；有三点共线可确定一个平面；任意三点不共线能确定1个或3个平面.所以四点可以确定1个或3个或无数个平面.‎ ‎[说明]公理3的简单应用.‎ 例4空间三条直线相交于一点，可以确定几个平面？‎ 空间四条直线相交于一点，可以确定几个平面？‎ 解：三条直线相交于一点可以确定1个或3个平面；‎ 四条直线相交于一点可以确定1个、4个或6个平面.‎ ‎[说明]推论2的简单应用.‎ 例5 如图，AB//CD，，求作BC与平面的交点.‎ α 解：连接EF和BC，交点即为所求BC与平面的交点.（公理3和公理2）‎ ‎[说明]推论3的简单应用.‎ 三、课堂小结 ‎1.公理1：确定直线在平面内；‎ ‎2.公理2：平面与平面相交于一直线；‎ ‎3.公理3和三个推论确定平面的条件；‎ 四、课后作业 练习14.1（1）2[来 练习14.1（2）1，2，3‎ 五、教学设计说明 本章呈现了几何研究的范围从平面扩展到空间时的基本方法.把几何研究的范围从平面扩展到空间后，增加了新的对象——平面.空间几何学是平面几何学的推广，平面几何中研究点与点、点与直线、直线与直线三种位置关系；空间几何中则增加了点与平面、直线与平面、平面与平面三中位置关系.本节的主要内容是让学生理解三个公理和三个推论，运用这些公理和推论进行一些简单的证明.‎ 公理是人们在长期的生活实践的观察和检验中发现的.可以联系生活中的情景来学习三个公理，从而帮助学生学习，加深他们对公理的理解.三个公理和三个推论是空间几何学习的基础，有了这个基础，才能进一步研究空间中点与面、线与面、面与面的位置关系和度量问题.‎