- 2021-06-15 发布 |
- 37.5 KB |
- 7页

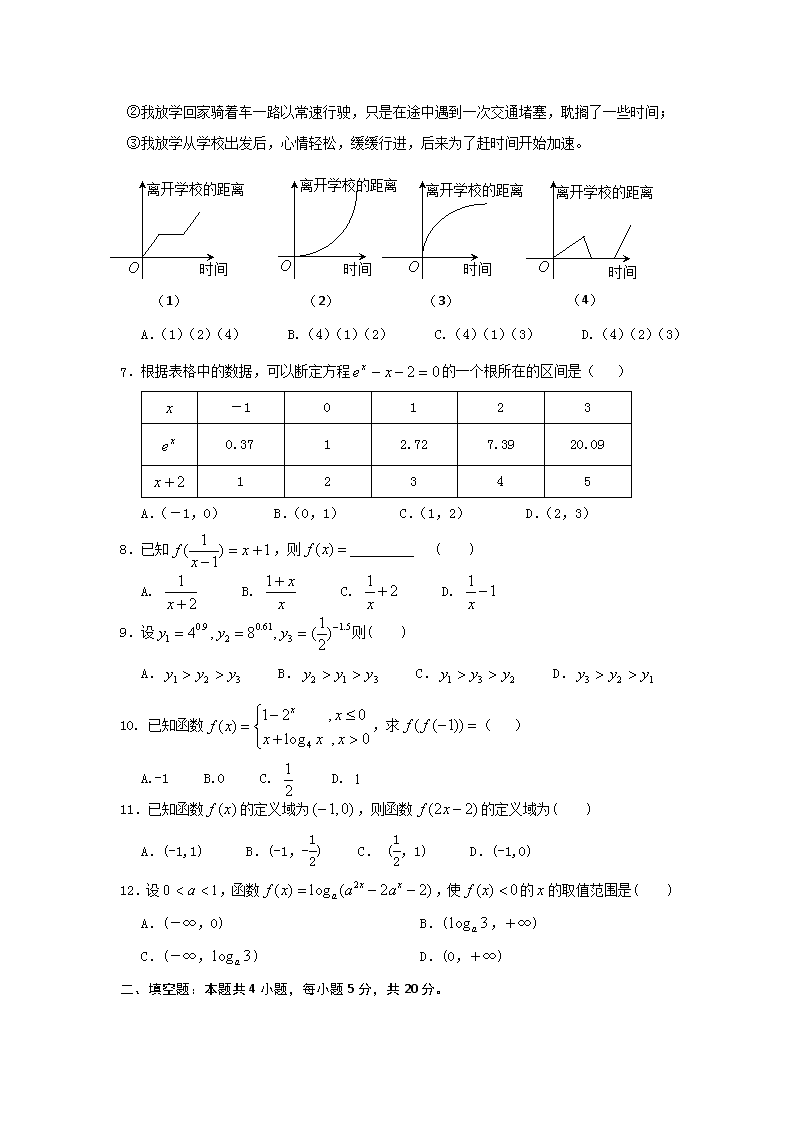

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年山东省师大附中高一上学期第一次学分认定(期中)考试数学试题
2018-2019学年山东省师大附中高一上学期第一次学分认定(期中)考试数学试题 本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页,满分为150分,考试用时120分钟。 注意事项: 1. 答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号、考试科目填写在规定的位置上。 2. 第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。 3. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置;如需改动,先划掉原来的答案,然后再写上新的答案,不得使用涂改液,胶带纸、修正带和其他笔。 一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。 1.下列对象能构成集合的是( ) A.高一年级全体较胖的学生 B.,,, C.全体很大的自然数 D.平面内到 三个顶点距离相等的所有点 2.函数的定义域为( ) A. B. C. D. 3.已知集合,则下列式子表示正确的有( ) ① ② ③ ④ A.1个 B.2个 C.3个 D.4个 4.下列函数中,在区间(0,+∞)上为增函数的是( ) A. B. C. D. 5. 已知函数的图象过定点,则点坐标为( ) A.(0,-1) B.(1,0) C.(0,0) D.(-1,0) 6.下列所给4个图象中,与所给3件事吻合最好的顺序为 ( ) ①我离开学校不久,发现自己把作业本忘在教室,于是立刻返回教室里取了作业本再回家; ②我放学回家骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间; (1) (2) (3) (4) 时间 时间 时间 时间 离开学校的距离 离开学校的距离 离开学校的距离 离开学校的距离 ③我放学从学校出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。 A.(1)(2)(4) B.(4)(1)(2) C.(4)(1)(3) D.(4)(2)(3) 7.根据表格中的数据,可以断定方程的一个根所在的区间是( ) -1 0 1 2 3 0.37 1 2.72 7.39 20.09 1 2 3 4 5 A.(-1,0) B.(0,1) C.(1,2) D.(2,3) 8.已知,则 ( ) A. B. C. D. 9.设则( ) A. B. C. D. 10. 已知函数,求( ) A.-1 B.0 C. D. 11.已知函数的定义域为,则函数的定义域为( ) A.(-1,1) B.(-1,-) C. (,1) D.(-1,0) 12.设,函数,使的的取值范围是( ) A.(-∞,0) B.(,+∞) C.(-∞,) D.(0,+∞) 二、填空题:本题共4小题,每小题5分,共20分。 13.已知幂函数的图象过点 . 14. 若是一次函数,且,则= .. 15.函数y=的值域是 . 16. 已知函数,若方程有四个不同的解,且,则的取值范围是____________. 三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。 17. (10分)集合,,求. 18.(12分)求值: (1) (2) 19.(12分)判断并证明函数在(0,2]内的单调性,并求其值域。 20.(12分)已知函数 (1) 判断并证明函数的奇偶性; (2) 当时函数与相同,且为偶函数,求的定义域及其表达式。 21.(12分)是定义在上的减函数,满足,, (1)求的值; (2)如果,求的取值范围。 22.(12分)已知函数,, (1)当时,求的值域; (2)设的最小值为,请写出的表达式,并求的解集。 山东师大附中2018级第一次学分认定考试数学答案 一、选择题: 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D C B A D B C C B B C C 二、填空题: (13) 3 (14) (15) [0,4) (16) 三、解答题: 17,解:,………………………………………………………………….2分 …………………………………………………………………2分 ……………………………………………..3分 ………………………………………3分 18,解: 19,解:函数在(0,2]内是减函数。……………………………………………2分 证明:任取,不妨设 因此,函数在(0,2]内是减函数。 由函数的单调性可得: ………………………………….2分 (2)解:由条件得,时, 21, 综上所述:查看更多