- 2021-06-15 发布 |
- 37.5 KB |
- 4页

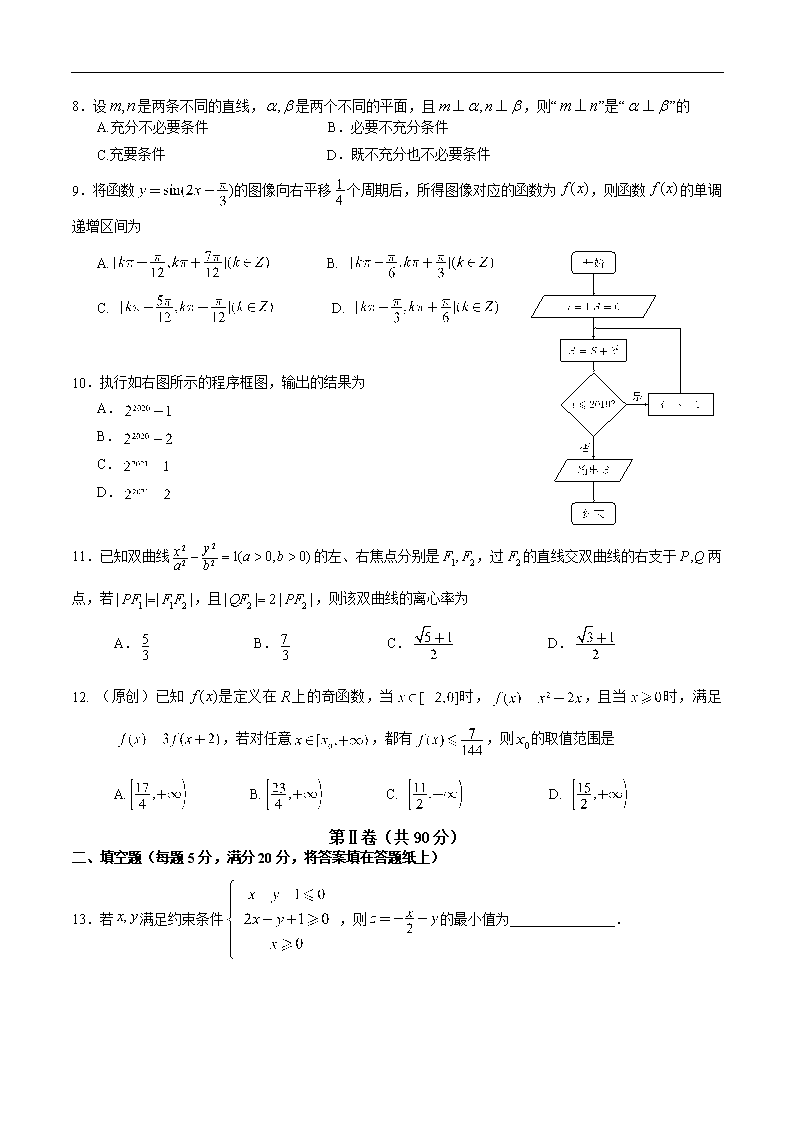
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020高三理科数学期末第06稿 (定稿)
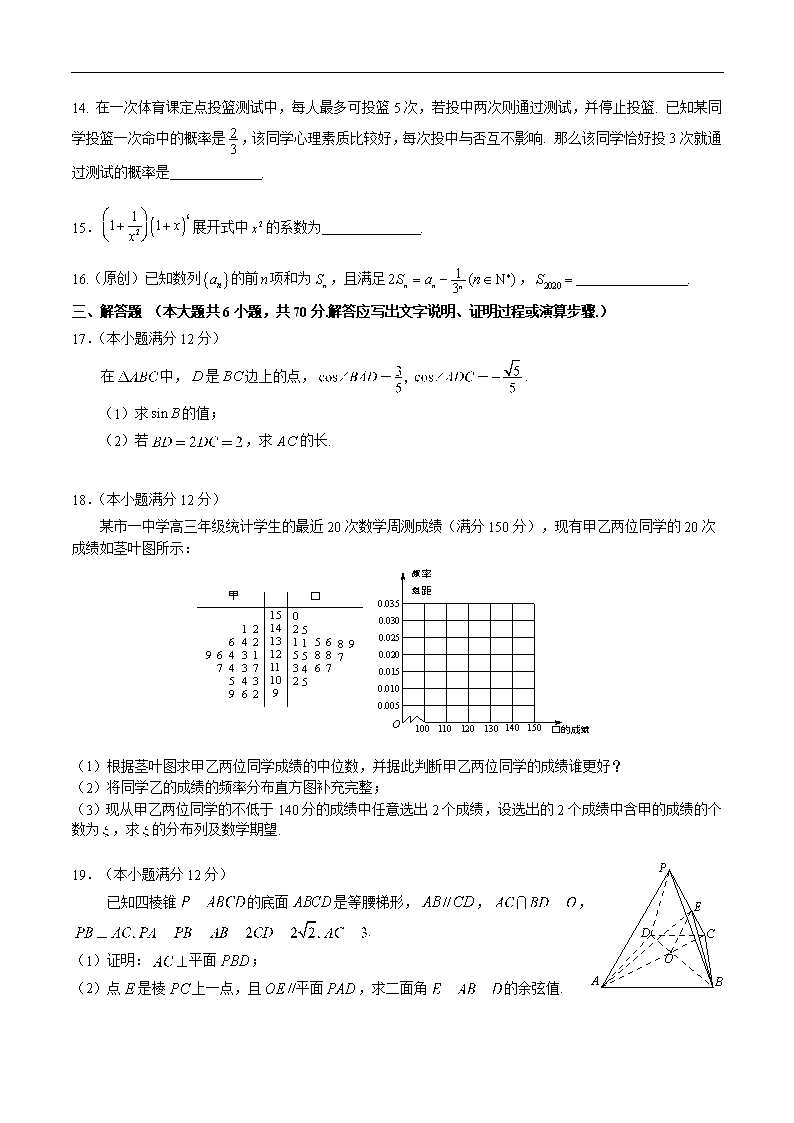
秘密★启用前 【考试时间:1 月 19 日】 2020年重庆一中高2020级高三上期期末考试 数 学(理科)试 题 卷 2020.1 注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。 2.作答时,将答案写在答题卡上。写在本试卷及草稿纸上无效。 3.考试结束后,将本试卷和答题卡一并交回。 第Ⅰ卷(共60分) 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知,,则 A. B. C. D. 2.复数在复平面内对应的点为 A. B. C. D. 3.已知向量,且,则 A. B. C.8 D. 4.圆的圆心到直线 的距离为2,则 A. B. C. D.2 5. 现有5人站成一排照相,其中甲、乙相邻,且丙、丁不相邻,则不同的站法有 A.12 种 B.24 种 C.36 种 D.48 种 6.已知,,,则 A. B. C. D. 7.(原创)《张丘建算经》是公元5世纪中国古代内容丰富的数学著作,书中卷上第二十三问:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问半月积几何?”其意思为“有个女子织布,每天比前一天多织相同量的布,第一天织五尺,一个月(按30天计)共织布9匹3丈.问:前半个月(按15天计)共织多少布?”已知1匹=4丈,1丈=10尺,可估算出前半个月一共织的布约有 A.195尺 B.133尺 C.130尺 D.135尺 8.设是两条不同的直线,是两个不同的平面,且,则“”是“”的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 9.将函数的图像向右平移个周期后,所得图像对应的函数为,则函数的单调递增区间为 A. B. C. D. 10.执行如右图所示的程序框图,输出的结果为 A. B. C. D. 11.已知双曲线的左、右焦点分别是,过的直线交双曲线的右支于两点,若,且,则该双曲线的离心率为 A. B. C. D. 12. (原创)已知是定义在上的奇函数,当时,,且当时,满足,若对任意,都有,则的取值范围是 A. B. C. D. 第Ⅱ卷(共90分) 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.若满足约束条件,则的最小值为_______________. 14. 在一次体育课定点投篮测试中,每人最多可投篮5次,若投中两次则通过测试,并停止投篮. 已知某同学投篮一次命中的概率是,该同学心理素质比较好,每次投中与否互不影响. 那么该同学恰好投3次就通过测试的概率是 . 15.展开式中的系数为 . 16.(原创)已知数列的前项和为,且满足, . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分12分) 在中,是边上的点,. (1)求的值; (2)若,求的长. 18.(本小题满分12分) 某市一中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示: (1)根据茎叶图求甲乙两位同学成绩的中位数,并据此判断甲乙两位同学的成绩谁更好? (2)将同学乙的成绩的频率分布直方图补充完整; (3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,设选出的2个成绩中含甲的成绩的个数为,求的分布列及数学期望. 19.(本小题满分12分) 已知四棱锥的底面是等腰梯形,//,, . (1)证明:平面; (2)点是棱上一点,且//平面,求二面角的余弦值. 20.(本小题满分12分) 已知点是坐标轴上两点,动点满足直线与的斜率之积为(其 中为常数,且). 记的轨迹为曲线. (1)求的方程,并说明是什么曲线; (2)过点斜率为的直线与曲线交于点,点在曲线上,且,若,求的取值范围. 21.(原创)(本小题满分12分) 已知函数. (1)设,(其中是的导数),求的最小值; (2)设,若有零点,求的取值范围. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.(本小题满分10分)选修4-4:坐标系与参数方程 在平面直角坐标系中,曲线的参数方程为(为参数). 以坐标原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为,若直线与曲线相切. (1)求曲线的极坐标方程; (2)在曲线上取两点与原点构成,且满足,求面积的最大值. 23.(本小题满分10分)选修4-5:不等式选讲 已知且. (1)若对任意正数恒成立,求的取值范围; (2)证明: 命题人:李长鸿 审题人:王 明 王中苏查看更多