2020届二轮复习直线平面平行的判定与性质课件（21张）（全国通用）

2020届二轮复习直线平面平行的判定与性质课件（21张）（全国通用）

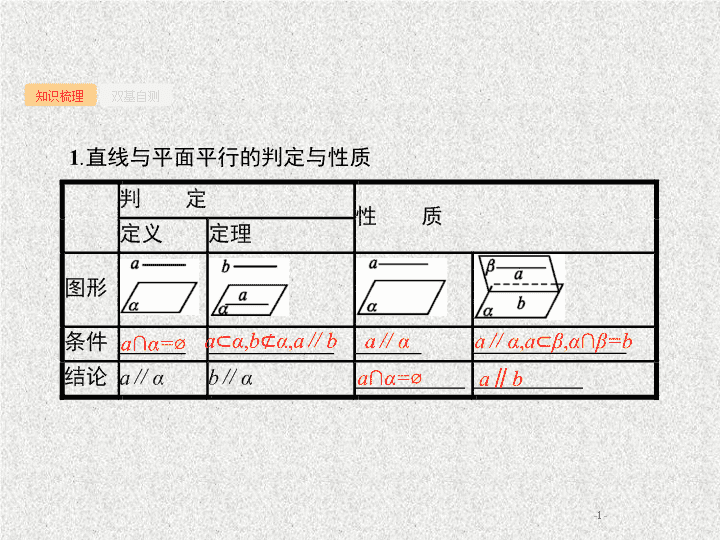
- 1 - 知识梳理 双基自测 1 . 直线与平面平行的判定与 性质 a ∩ α = ⌀ 　 a ⊂ α , b ⊄ α , a ∥ b 　 a ∥ α a ∥ α , a ⊂ β , α ∩ β =b a ∩ α = ⌀ 　 a ∥ b - 2 - 知识梳理 双基自测 2 . 面面平行的判定与 性质 α ∩ β = ⌀ a ⊂ β , b ⊂ β , a ∩ b=P , a ∥ α , b ∥ α 　 α ∥ β , α ∩ γ =a , β ∩ γ =b - 3 - 知识梳理 双基自测 3 . 常用结论 (1) 两个平面平行的有关结论 ① 垂直于同一条直线的两个平面平行 , 即若 a ⊥ α , a ⊥ β , 则 α ∥ β . ② 平行于同一平面的两个平面平行 , 即若 α ∥ β , β ∥ γ , 则 α ∥ γ . (2) 在推证线面平行时 , 一定要强调直线不在平面内 , 否则会出现错误 . 2 - 4 - 知识梳理 双基自测 3 4 1 5 1 . 下列结论正确的打 “ √ ” , 错误的打 “ ×” . (1) 若一条直线平行于一个平面内的一条直线 , 则这条直线平行于这个平面 . ( 　　 ) (2) 若一条直线平行于一个平面 , 则这条直线平行于这个平面内的任一条直线 . ( 　　 ) (3) 若直线 a 与平面 α 内无数条直线平行 , 则 a ∥ α . ( 　　 ) (4) 如果一个平面内的两条直线平行于另一个平面 , 那么这两个平面平行 . ( 　　 ) (5) 如果两个平面平行 , 那么分别在这两个平面内的两条直线平行或异面 . ( 　　 ) × × × × √ - 5 - 知识梳理 双基自测 2 3 4 1 5 2 . 已知正方体 ABCD-A 1 B 1 C 1 D 1 , 下列结论中 , 正确的是 　　　 ( 填序号 ) .   ① AD 1 ∥ BC 1 ; ② 平面 AB 1 D 1 ∥ 平面 BDC 1 ; ③ AD 1 ∥ DC 1 ; ④ AD 1 ∥ 平面 BDC 1 . ①② ④ - 6 - 知识梳理 双基自测 2 3 4 1 5 解析 如图 . 因为 AB C 1 D 1 , 所以四边形 AD 1 C 1 B 为平行四边形 . 故 AD 1 ∥ BC 1 , 从而 ① 正确 ; 易证 BD ∥ B 1 D 1 , AB 1 ∥ DC 1 , 又 AB 1 ∩ B 1 D 1 =B 1 , BD ∩ DC 1 =D , 故平面 AB 1 D 1 ∥ 平面 BDC 1 , 从而 ② 正确 ; 由图易知 AD 1 与 DC 1 异面 , 故 ③ 错误 ; 因 AD 1 ∥ BC 1 , AD 1 ⊄ 平面 BDC 1 , BC 1 ⊂ 平面 BDC 1 , 故 AD 1 ∥ 平面 BDC 1 , 故 ④ 正确 . - 7 - 知识梳理 双基自测 2 3 4 1 5 3 . 已知 P 是正方体 ABCD-A 1 B 1 C 1 D 1 棱 DD 1 上任意一点 ( 不与端点重合 ), 则 该 在 正方体的 12 条棱中 , 与平面 ABP 平行的直线是 　　　　 . DC , D 1 C 1 , A 1 B 1 解析 DC , D 1 C 1 , A 1 B 1 均平行于直线 AB , 依据直线与平面平行判定定理 , 均可证明它们平行于平面 ABP. - 8 - 知识梳理 双基自测 2 3 4 1 5 4 . 在 四面体 ABCD 中 , M , N 分别是平面 △ ACD , △ BCD 的重心 , 则四面体的四个面中与 MN 平行的是 　 .   平面 ABC 、平面 ABD 解析 如图 , 连接 AM 并延长交 CD 于点 E , 连接 BN 并延长交 CD 于点 F. 由重心性质可知 , E , F 重合为一点 , 且该点为 CD 的中点 E , 由 , 得 MN ∥ AB , 因此 , MN ∥ 平面 ABC , 且 MN ∥ 平面 ABD. - 9 - 知识梳理 双基自测 2 3 4 1 5 5 . 如图所示 , 在正四棱柱 ABCD-A 1 B 1 C 1 D 1 中 , E , F , G , H 分别是棱 CC 1 , C 1 D 1 , D 1 D , DC 的中点 , N 是 BC 的中点 , 点 M 在四边形 EFGH 及其内部运动 , 则 M 满足条件 　　　　　　　　　　 时 , 有 MN ∥ 平面 B 1 BDD 1 .   M ∈ 线段 FH 解析 由题意易知平面 HNF ∥ 平面 B 1 BDD 1 , 当点 M 满足在线段 FH 上有 MN ∥ 平面 B 1 BDD 1 . - 10 - 考点 1 考点 2 考点 3 例 1 (1) 设 m , n 是两条不同的直线 , α , β 是两个不同的平面 , 下列命题中正确的是 ( 　　 ) A. 若 α ⊥ β , m ⊂ α , n ⊂ β , 则 m ⊥ n B . 若 α ∥ β , m ⊂ α , n ⊂ β , 则 m ∥ n C. 若 m ⊥ n , m ⊂ α , n ⊂ β , 则 α ⊥ β D . 若 m ⊥ α , m ∥ n , n ∥ β , 则 α ⊥ β (2) 设 m , n 表示不同直线 , α , β 表示不同平面 , 则下列结论中正确的是 ( 　　 ) A. 若 m ∥ α , m ∥ n , 则 n ∥ α B. 若 m ⊂ α , n ⊂ β , m ∥ β , n ∥ α , 则 α ∥ β C. 若 α ∥ β , m ∥ α , m ∥ n , 则 n ∥ β D. 若 α ∥ β , m ∥ α , n ∥ m , n ⊄ β , 则 n ∥ β 思考 如何借助几何模型来找平行关系 ? 答案 解析 解析 关闭 (1)A 中 , m 与 n 可相交、可异面、可平行 ;B 中 , m 与 n 可平行、可异面 ;C 中 , 若 α ∥ β , 仍然可满足 m ⊥ n , m ⊂ α , n ⊂ β , 故 C 错误 ; 故 D 正确 . (2)A 错误 , n 有可能在平面 α 内 ;B 错误 , 平面 α 有可能与平面 β 相交 ;C 错误 , n 也有可能在平面 β 内 ;D 正确 , 易知 m ∥ β 或 m ⊂ β , 若 m ⊂ β , 又 n ∥ m , n ⊄ β , ∴ n ∥ β , 若 m ∥ β , 过 m 作平面 γ 交平面 β 于直线 l , 则 m ∥ l , 又 n ∥ m , ∴ n ∥ l , 又 n ⊄ β , l ⊂ β , ∴ n ∥ β. 答案 解析 关闭 (1)D 　 (2)D 　 - 11 - 考点 1 考点 2 考点 3 解题心得 线面平行、面面平行的命题真假判断多以小题出现 , 处理方法是数形结合 , 画图或结合正方体等有关模型来解题 . - 12 - 考点 1 考点 2 考点 3 对点训练 1 (1) 若直线 a ⊥ b , 且直线 a ∥ 平面 α , 则直线 b 与平面 α 的位置关系是 ( 　　 ) A. b ⊂ α B. b ∥ α C. b ⊂ α 或 b ∥ α D. b 与 α 相交或 b ⊂ α 或 b ∥ α (2) 给出下列关于互不相同的直线 l , m , n 和平面 α , β , γ 的三个命题 : ① 若 l 与 m 为异面直线 , l ⊂ α , m ⊂ β , 则 α ∥ β ; ② 若 α ⊥ β , l ⊂ α , m ⊂ β , 则 l ∥ m ; ③ 若 α ∩ β =l , β ∩ γ =m , γ ∩ α =n , l ∥ γ , 则 m ∥ n. 其中真命题的个数为 ( 　　 ) A.3 B.2 C.1 D.0 答案 解析 解析 关闭 (1) 可以构造一草图来表示位置关系 , 经验证 , 当 b 与 α 相交或 b ⊂ α 或 b ∥ α 时 , 均可满足直线 a ⊥ b , 且直线 a ∥平面 α 的情况 , 故选 D. (2) ① 中 , 当 α 与 β 相交时 , 也能存在符合题意的 l , m ; ② 中 , l 与 m 也可能异面 ; ③ 中 , l ∥ γ , l ⊂ β , β ∩ γ=m ⇒ l ∥ m , 同理 l ∥ n , 则 m ∥ n , 正确 . 答案 解析 关闭 (1)D 　 (2)C - 13 - 考点 1 考点 2 考点 3 例 2 如图 , 在三棱柱 ABC-A 1 B 1 C 1 中 , AA 1 ⊥ 平面 ABC , AC ⊥ BC , AC=BC=CC 1 = 2 , 点 D 为 AB 的中点 . (1) 证明 : AC 1 ∥ 平面 B 1 CD ; (2) 若 P , Q 分别是 △ A 1 CD 与 △ B 1 CD 的重心 , 证明 : PQ ∥ 平面 ABC. 思考 证明线面平行的关键是什么 ? - 14 - 考点 1 考点 2 考点 3 证明 (1) 方法一 ( 判定定理法 )   连接 BC 1 , 交 B 1 C 于点 O , 连接 OD. 在三棱柱 ABC-A 1 B 1 C 1 中 , 四边形 BCC 1 B 1 是平行四边形 . ∴ 点 O 是 BC 1 的中点 . ∵ 点 D 为 AB 的中点 , ∴ OD ∥ AC 1 . 又 OD ⊂ 平面 B 1 CD , AC 1 ⊄ 平面 B 1 CD , ∴ AC 1 ∥ 平面 B 1 CD. - 15 - 考点 1 考点 2 考点 3 方法二 ( 性质定理法 ) 如图 , 取 A 1 B 1 的中点 D 1 , 连接 C 1 D 1 , AD 1 , DD 1 . 在矩形 ABB 1 A 1 中 , AD=DB , A 1 D 1 =D 1 B 1 , 所以 AD 1 ∥ DB 1 , 且 DD 1 BB 1 . 又因为 BB 1 CC 1 , 所以 DD 1 CC 1 , 所以四边形 CDD 1 C 1 是平行四边形 , 所以 C 1 D 1 ∥ CD. 又因为 C 1 D 1 ⊂ 平面 AC 1 D 1 , CD ⊄ 平面 AC 1 D 1 , 所以 CD ∥ 平面 AC 1 D 1 . 同理 , B 1 D ∥ 平面 AC 1 D 1 . 因为 B 1 D ∩ CD=D , 所以平面 B 1 CD ∥ 平面 AC 1 D 1 . 因为 AC 1 ⊂ 平面 AC 1 D 1 , 所以 AC 1 ∥ 平面 B 1 CD. - 16 - 考点 1 考点 2 考点 3 (2) 如图 , 因为 P 是 △ A 1 CD 的重心 , 连接 A 1 P 并延长 , 交 CD 于点 M , 则 M 为 CD 的中点 . 同理连接 B 1 Q , 并延长 , 与 CD 也相交于点 M. 又因为 AB ∥ A 1 B 1 , 所以 PQ ∥ AB. 因为 PQ ⊄ 平面 ABC , AB ⊂ 平面 ABC , 所以 PQ ∥ 平面 ABC. - 17 - 考点 1 考点 2 考点 3 解题心得 证明线面平行的关键点及探求线线平行的方法 : (1) 证明直线与平面平行的关键是设法在平面内找到一条与已知直线平行的直线 ; (2) 利用几何体的特征 , 合理利用中位线定理、线面平行的性质 , 或者构造平行四边形、寻找比例式证明两直线平行 ; (3) 注意说明已知的直线不在平面内 , 即三个条件缺一不可 . - 18 - 考点 1 考点 2 考点 3 对点训练 2 如图 , 在四棱锥 S-ABCD 中 , 四边形 ABCD 为矩形 , E 为 SA 的中点 , SA=SB= 2, AB= 2 , BC= 3 . ( 1) 证明 : SC ∥ 平面 BDE ; (2) 若 BC ⊥ SB , 求三棱锥 C-BDE 的体积 . - 19 - 考点 1 考点 2 考点 3 (1) 证明 连接 AC , 设 AC ∩ BD=O , 连接 OE. ∵ 四边形 ABCD 为矩形 , ∴ O 为 AC 的中点 , 在 △ ASC 中 , E 为 AS 的中点 , ∴ SC ∥ OE , 又 OE ⊂ 平面 BDE , SC ⊄ 平面 BDE , ∴ SC ∥ 平面 BDE. - 20 - 考点 1 考点 2 考点 3 (2) 解 过点 E 作 EH ⊥ AB , 垂足为 H , ∵ BC ⊥ AB , 且 BC ⊥ SB , AB ∩ SB=B , ∴ BC ⊥ 平面 SAB , ∵ EH ⊂ 平面 ABS , ∴ EH ⊥ BC , 又 EH ⊥ AB , AB ∩ BC=B , ∴ EH ⊥ 平面 ABCD , 在 △ SAB 中 , 取 AB 中点 M , 连接 SM , ∵ SA=SB , ∴ SM ⊥ AB , ∴ SM= 1 . - 21 - 考点 1 考点 2 考点 3 例 3 如图 , 四棱柱 ABCD-A 1 B 1 C 1 D 1 的底面 ABCD 是正方形 . ( 1) 证明 : 平面 A 1 BD ∥ 平面 CD 1 B 1 ; (2) 若平面 ABCD ∩ 平面 B 1 D 1 C= 直线 l , 证明 : B 1 D 1 ∥ l. 思考 证明面面平行的常用方法有哪些 ?