【北师大版】2021版高考数学一轮复习第九章立体几何9.7.2 利用空间向量求二面角与空间距离
- 1 -
9.7.2 利用空间向量求二面角与空间距离
核心考点·精准研析
考点一 求二面角
命
题
精
解
读
1.考什么:(1)考查与二面角相关的问题.(2)考查直观想象与数学运算的核心素
养.
2.怎么考:以柱、锥、台等几何体为载体考查与二面角相关的证明、求值问题.
3.新趋势:以求二面角或某一三角函数值为主要命题方向.
学
霸
好
方
法
1.利用空间向量求二面角的两种方法:
(1)分别在二面角的两个半平面内找到一个与棱垂直且从垂足出发的两个向量,则
这两个向量的夹角的大小就是二面角的平面角的大小;
(2)通过平面的法向量来求:设二面角的两个半平面的法向量分别为 n1 和 n2,则二
面角的大小等于
(或π-).
2.交汇问题: 常常与证明线面的平行、垂直关系同时考查.
求二面角或某一三角函数值
【典例】 (2019·全国卷Ⅱ)如图,长方体 ABCD-A1B1C1D1 的底面 ABCD 是正方形,点 E 在棱 AA1 上,BE⊥EC1.
(1)证明:BE⊥平面 EB1C1.
(2)若 AE=A1E,求二面角 B-EC-C1 的正弦值.
【解析】(1)由已知得,B1C1⊥平面 ABB1A1,BE 平面 ABB1A1,故 B1C1⊥BE.又 BE⊥EC1,EC1∩B1C1=C1,
所以 BE⊥平面 EB1C1.
(2)由(1)知∠BEB1=90°.由题设知 Rt△ABE≌Rt△A1B1E,所以∠AEB=45°,故 AE=AB,AA1=2AB.以 D 为坐标原
点, 的方向为 x 轴正方向,| |为单位长,建立如图所示的空间直角坐标系 D-xyz,
- 2 -
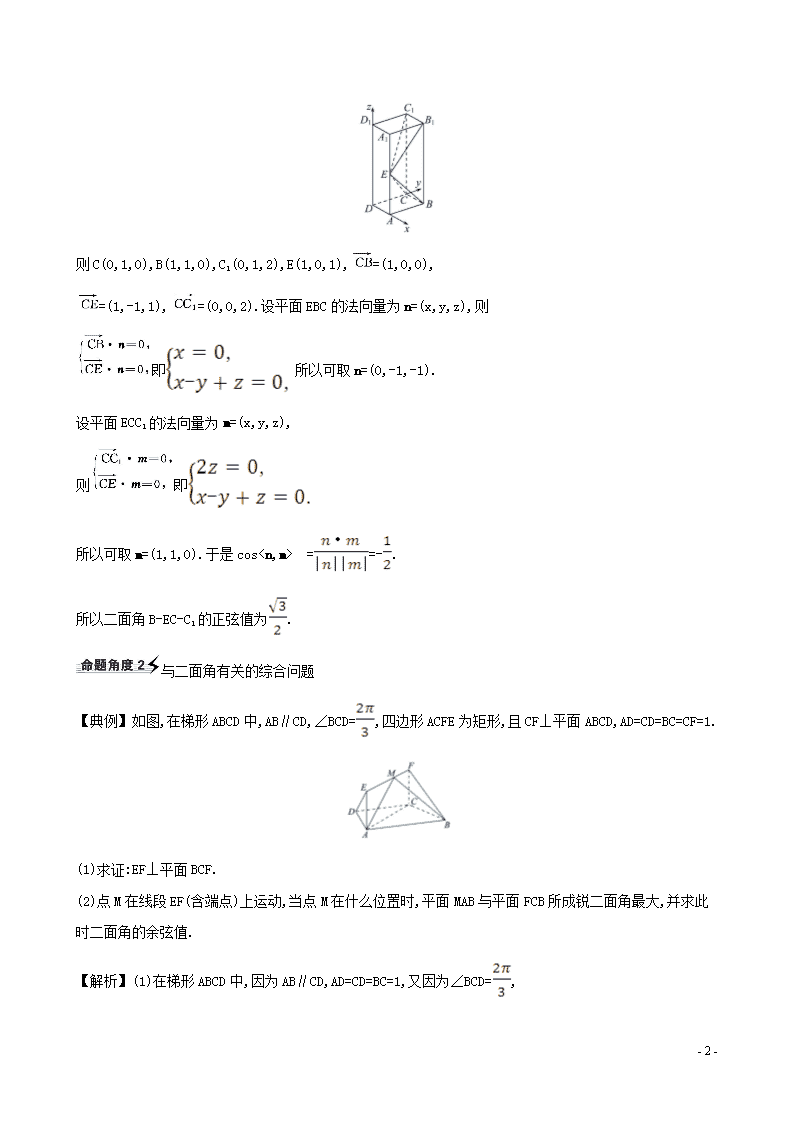
则 C(0,1,0),B(1,1,0),C1(0,1,2),E(1,0,1), =(1,0,0),
=(1,-1,1), =(0,0,2).设平面 EBC 的法向量为 n=(x,y,z),则
即 所以可取 n=(0,-1,-1).
设平面 ECC1 的法向量为 m=(x,y,z),
则 即
所以可取 m=(1,1,0).于是 cos = =- .
所以二面角 B-EC-C1 的正弦值为 .
与二面角有关的综合问题
【典例】如图,在梯形 ABCD 中,AB∥CD,∠BCD= ,四边形 ACFE 为矩形,且 CF⊥平面 ABCD,AD=CD=BC=CF=1.
(1)求证:EF⊥平面 BCF.
(2)点 M 在线段 EF(含端点)上运动,当点 M 在什么位置时,平面 MAB 与平面 FCB 所成锐二面角最大,并求此时
二面角的余弦值.
【解析】(1)在梯形 ABCD 中,因为 AB∥CD,AD=CD=BC=1,又因为∠BCD= ,
- 3 -
所以∠ADC= π,∠ACD= ,所以∠ACB= ,故 AC⊥BC.
因为 CF⊥平面 ABCD,AC 平面 ABCD,
所以 AC⊥CF,
而 CF∩BC=C,所以 AC⊥平面 BCF,因为 EF∥AC,所以 EF⊥平面 BCF.
(2)由(1)可建立分别以直线 CA,CB,CF 为 x 轴,y 轴,z 轴的空间直角坐标系如图所示,
AD=CD=BC=CF=1,
令 FM=λ(0≤λ≤ ),
则 C(0,0,0),A( ,0,0),B(0,1,0),M(λ,0,1),
所以 =(- ,1,0), =(λ,-1,1),
设 n1=(x,y,z)为平面 MAB 的一个法向量,
由 得
取 x=1,则 n1=(1, , -λ),
因为 n2=(1,0,0)是平面 FCB 的一个法向量,
所以 cos θ= =
= ,
因为 0≤λ≤ ,所以当λ=0 时,cos θ有最小值 ,所以点 M 与点 F 重合时,平面 MAB 与平面 FCB 所成锐
二面角最大,此时二面角的余弦值为 .
- 4 -
1.在正方体 ABCD-A1B1C1D1 中,点 E 为 BB1 的中点,则平面 A1ED 与平面 ABCD 所成的锐二面角的余弦值为
( )
A. B. C. D.
【解析】选 B.以 A 为原点建立如图所示的空间直角坐标系 A-xyz,设棱长为 1,则
A1(0,0,1),E 1,0, ,D(0,1,0),
所以 =(0,1,-1), = 1,0,- ,
设平面 A1ED 的一个法向量为 n1=(1,y,z),
则 所以
所以 n1=(1,2,2).因为平面 ABCD 的一个法向量为 n2=(0,0,1),所以 cos= = .
即所成的锐二面角的余弦值为 .
2.如图,四棱锥 P ABCD 中,底面 ABCD 是正方形,PD⊥平面 ABCD 且 PD=AD=2,点 E 是射线 AB 上一点,当二面
角 P-EC-D 为 时,AE= ( )
- 5 -
A.1 B. C.2- D.2 +2
【解析】选 D.设 AE=a(a≥0),以点 D 为原点,DA,DC,DP 所在直线分别为 x,y,z 轴建立空间直角坐标系,则
D(0,0,0),C(0,2,0),E(2,a,0),P(0,0,2),则 =(0,2,-2), =(2,a,-2),设平面 PEC 的法向量为
m=(x,y,z),则 即 故 x∶y∶z=(2-a)∶2∶2,
故令 m=(2-a,2,2),
设平面 ECD 的法向量为 n=(0,0,1),
二面角 P EC D 的平面角θ= ,
所以 cosθ= = = ,
所以 a=2 +2 或 a=-2 +2(舍去),
故 AE=2 +2.
1.在矩形 ABCD 中,AB=4,BC=3,沿对角线 AC 把矩形折成二面角 D-AC-B 的平面角为 60°
时,BD=________________.
【解析】在矩形 ABCD 中,AB=4,BC=3,
过点 D 作 DE⊥AC 于点 E,
过点 B 作 BF⊥AC 于点 F,
则| |=| |= = ,
| |=5-2× = .
沿对角线 AC 把矩形折成二面角 D-AC-B 的平面角为 60°时,
则 = + + ,
- 6 -
= + + +2 · +2 · +2 ·
= ×2+ +0+0+2× × ×cos(180°-60°)= .
所以,BD= .
答案:
2.(2019·全国卷Ⅲ)图 1 是由矩形 ADEB,Rt△ABC 和菱形 BFGC 组成的一个平面图形,其中 AB=1,BE=BF=2,
∠FBC=60°,将其沿 AB,BC 折起使得 BE 与 BF 重合,连接 DG,如图 2.
(1)证明:图 2 中的 A,C,G,D 四点共面,且平面 ABC⊥平面 BCGE.
(2)求图 2 中的二面角 B-CG-A 的大小.
【解析】(1)由已知得 AD∥BE,CG∥BE,所以 AD∥CG,故 AD,CG 确定一个平面,从而 A,C,G,D 四点共面.
由已知得 AB⊥BE,AB⊥BC,BE∩BC=B,
故 AB⊥平面 BCGE.
又因为 AB 平面 ABC,所以平面 ABC⊥平面 BCGE.
(2)作 EH⊥BC,垂足为 H.因为 EH 平面 BCGE,平面 BCGE⊥平面 ABC,所以 EH⊥平面 ABC.
由已知,菱形 BCGE 的边长为 2,∠EBC=60°,可求得 BH=1,EH= .
以 H 为坐标原点, 的方向为 x 轴的正方向,建立如图所示的空间直角坐标系 H-xyz,
则 A(-1,1,0),C(1,0,0),G(2,0, ), =(1,0, ), =(2,-1,0).
- 7 -
设平面 ACGD 的法向量为 n=(x,y,z),
则 即
所以可取 n=(3,6,- ).
又平面 BCGE 的法向量可取为 m=(0,1,0),
所以 cos n,m = = .
因此二面角 B-CG-A 的大小为 30°.
考点二 求空间距离
【典例】1.设正方体 ABCD-A1B1C1D1 的棱长为 2,则点 D1 到平面 A1BD 的距离是________________.
2.已知斜三棱柱 ABC-A1B1C1 的侧面 A1ACC1 与底面 ABC 垂直,∠ABC=90°,BC=2,
AC=2 ,且 AA1⊥A1C,AA1=A1C.
(1)求这个三棱柱的体积.
(2)求顶点 C 到侧面 A1ABB1 的距离.
【解题导思】
序号 联想解题
1 在正方体中,求点 D1 到平面 A1BD 的距离,首先想到利用向量法.
2 观察所给图形,想到尝试利用转化法或等体积法.
【解析】1.如图建立空间直角坐标系,
则 D1(0,0,2),A1(2,0,2),D(0,0,0),B(2,2,0),
- 8 -
所以 =(2,0,0), =(2,0,2), =(2,2,0),
设平面 A1BD 的一个法向量 n=(x,y,z),
则 .令 x=1,则 n=(1,-1,-1),所以点 D1 到平面 A1BD 的距离
d= = = .
答案:
2.(1)取 AC 的中点 D,连接 A1D,因为 AA1⊥A1C,AA1=A1C,AC=2 ,所以 A1D⊥AC,A1D= ,又因为侧面 A1ACC1
与底面 ABC 垂直,所以 A1D⊥底面 ABC,所以 A1D 就是三棱柱的高,因为∠ABC=90°,BC=2,AC=2 ,所以
AB=2 ,所以底面积为 S△ABC= ×2 ×2=2 ,所以三棱柱的体积为 V=S△ABC·A1D=2 × =2 .
(2)等体积法:连接 A1B,
根据定义,点 C 到面 A1ABB1 的距离,即为三棱锥 C-A1AB 的高 h,由 =
得 ·h= S△ABC·A1D,
即 ×2 h= ×2 × ,所以 h= 为所求.
求点到平面的距离的常用方法
(1)直接法:过 P 点作平面α的垂线,垂足为 Q,把 PQ 放在某个三角形中,解三角形求出 PQ 的长度就是点 P
到平面α的距离.
(2)转化法:若点 P 所在的直线 l 平行于平面α,则转化为直线 l 上某一个点到平面α的距离来求.
(3)等体积法:求点面距离可以转化为求三棱锥的高,如四面体中点 A 到平面 BCD 的距离,用等体积法求得
h= .
- 9 -
(4)向量法:设平面α的一个法向量为 n,A 是α内任意点,则点 P 到α的距离为 d= .
如图,△BCD 与△MCD 都是边长为 2 的正三角形,平面 MCD⊥平面 BCD,AB⊥平面 BCD,AB=2 ,求点 A 到平面
MBC 的距离.
【解析】如图,取 CD 的中点 O,连接 OB,OM,
因为△BCD 与△MCD 均为正三角形,所以 OB⊥CD,OM⊥CD,又平面 MCD⊥平面 BCD,所以 MO⊥平面 BCD.
以 O 为坐标原点,直线 OC,BO,OM 分别为 x 轴,y 轴,z 轴,建立空间直角坐标系 O-xyz.
因为△BCD 与△MCD 都是边长为 2 的正三角形,所以 OB=OM= ,则
O(0,0,0),C(1,0,0),M(0,0, ),B(0,- ,0),A(0,- ,2 ),
所以 =(1, ,0), =(0, , ).
设平面 MBC 的法向量为 n=(x,y,z),
由 得 即 取 x= ,可得平面 MBC 的一个法向
量为 n=( ,-1,1).
- 10 -
又 =(0,0,2 ),
所以所求距离为 d= = .