数学理卷·2018届福建省龙海第二中学高二上学期期末考试(2017-01)
龙海二中 2016-2017 学年上学期期末考试
高二数学(理科)试卷
(考试时间:120 分钟 总分:150 分)
一、选择题(本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的 A、B、C、D 的四个
选项中,只有一个选项是符合题目要求的,请将正确答案的字母代号填到答题卷相应位置.)
1.高三(1)班有学生 52 人,现将所有学生随机编号,用系统抽样方法,抽取一个容量为 4
的样本,已知 5 号、31 号、44 号学生在样本中,则样本中还有一个学生的编号是( )
A.8 B.13 C.15 D.18
2.下列命题中,真命题是( )
A.∀x∈R,x2>0 B.∀x∈R, 1
1i i= +
输出s
结束
否
是
第 6 题
2( 1)s s= +
A.在区间( 2,1)上 f(x)是增函数
B.在(1,3)上 f(x)是减函数
C.在(4,5)上 f(x)是增函数
D.当 x=4 时,f(x)取极大值
10.函数 是定义域为 的函数,对任意实数 都有 成立.若当
时 , 不 等 式 成 立 , 设 , ,
,则 , , 的大小关系是 ( )
A. B. C. D.
11.如图,在正三棱柱 中,若 , 则异面直线 与 所成
角的余弦值为( )
A. B. C. D.
12. 为 坐 标 原 点 , 为 抛 物 线 的 焦 点 , 为 上 一 点 ,若
,则 的面积为 ( )
A. B. C. D.
二、填空题(本大题共 4 个小题,每小题 5 分,共 20 分.请将答案填在答题卷相应横线上.)
13. 已 知 命 题 : 任 意 , 则 非 是
_________________________ .
14. 正方体 的 棱长为 ,在正方体内随机取一点 ,则点 落
在三棱锥 内的概率为 .
15. 已知 为原点,椭圆 上一点 到左焦点 的距离为 4, 是 的中点.则
= .
16.对于函数
(1) 是 的单调递减区间; (2) 是 的极小值,
是 的极大值; (3) 有最大值,没有最小值; (4) 没有最大值,也没有
最小值.其中判断正确的是 .
三、解答题(本大题共 6 题,共 70 分.解答须写出说明、证明过程和演算步骤.解答写在答题卡
( )f x x ( ) (2 )f x f x= −
1x ≠ ( 1) ( ) 0x f x′− ⋅ < (0.5)a f= 4( )3b f=
(3)c f= a b c
b a c> > cba >> abc >> bca >>
−
R
ABC A B C′ ′ ′− 2AA AB′ = AB′ BC′
0 3
8
3
5
7
10
O F 2: 4 2C y x= P C
4 2PF = POF∆
2 2 2 2 3 4
p ,sin 1x R x∈ ≤ p
1111 DCBAABCD − a M M
111 BCAB −
O
2 2
125 9
x y+ = P 1F M 1PF
OM
2( ) (2 ) xf x x x e= −
( 2, 2)− ( )f x ( 2)f − ( )f x ( 2)f
( )f x ( )f x ( )f x
(第 9 题图)
上的指定区域内.)
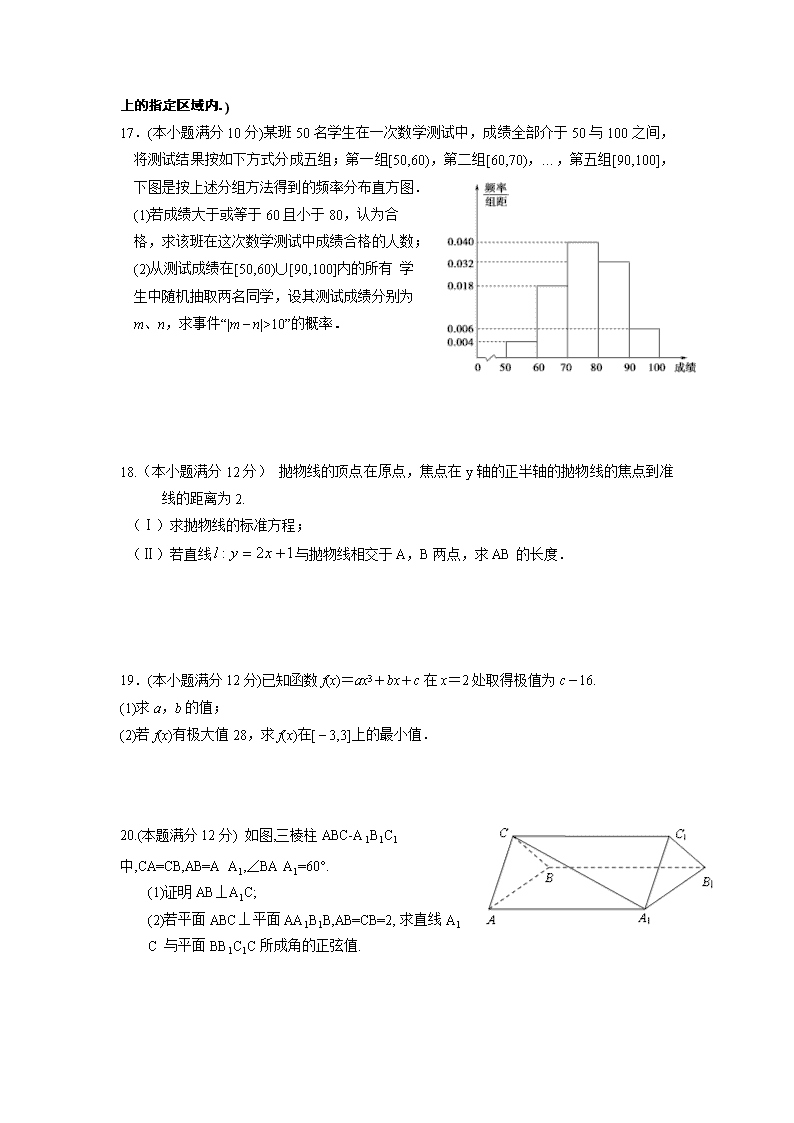
17.(本小题满分 10 分)某班 50 名学生在一次数学测试中,成绩全部介于 50 与 100 之间,
将测试结果按如下方式分成五组;第一组[50,60),第二组[60,70),…,第五组[90,100],
下图是按上述分组方法得到的频率分布直方图.
(1)若成绩大于或等于 60 且小于 80,认为合
格,求该班在这次数学测试中成绩合格的人数;
(2)从测试成绩在[50,60)∪[90,100]内的所有 学
生中随机抽取两名同学,设其测试成绩分别为
m、n,求事件“|m n|>10”的概率.
18.(本小题满分 12 分) 抛物线的顶点在原点,焦点在 y 轴的正半轴的抛物线的焦点到准
线的距离为 2.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)若直线 与抛物线相交于 A,B 两点,求 AB 的长度.
19.(本小题满分 12 分)已知函数 f(x)=ax3+bx+c 在 x=2 处取得极值为 c 16.
(1)求 a,b 的值;
(2)若 f(x)有极大值 28,求 f(x)在[ 3,3]上的最小值.
20.(本题满分 12 分) 如图,三棱柱 ABC-A1B1C1
中,CA=CB,AB=A A1,∠BA A1=60°.
(1)证明 AB⊥A1C;
(2)若平面 ABC⊥平面 AA1B1B,AB=CB=2,求直线 A1
C 与平面 BB1C1C 所成角的正弦值.
−
12: += xyl
−
−
x
y
C
B
NM
T
O
A
21.( 本 题 满
分 12 分)已
知 函 数
.
(Ⅰ)若曲线 在点 处的切线与直线 垂直,求函数 的
单调区间;
(Ⅱ)若对于 都有 成立,试求 的取值范围;
22.(本题满分 12 分)如图,圆 与 轴相切于点 ,与 轴正半轴相交于两点
(点 在点 的左侧),且 .
(Ⅰ)求圆 的方程;
(Ⅱ)过点 任作一条直线与椭圆 相交于两点
,连接 ,求证: .
龙海二中 2016-2017 学年上学期期末考试
高二数学(理科)参考答案
2( ) ln 2 0)f x a x ax
= + − > (
( )y f x= (1, (1))P f 2y x= + ( )y f x=
(0, )x∀ ∈ +∞ ( ) 2( 1)f x a> − a
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D D B A A C B A C A D C
C y ( )0,2T x
,M N M N 3MN =
C
M
2 2
: 14 8
x yΓ + =
A B、 AN BN、 ANM BNM∠ = ∠
13.存在 14.. 15. 3 16.②③
17. (1)由直方图知,成绩在[60,80)内的人数为 50×10×(0.018+0.040)=29,
所以该班在这次数学测试中成绩合格的有 29 人..............4 分
(2)由直方图知,成绩在[50,60)的人数为 50×10×0.004=2,设成绩为 x、y;成绩在[90,100]
的人数为 50×10×0.006=3,设成绩为 a、b、c,
若 m、n∈[50,60),则只有 xy 一种情况..............5 分
若 m、n∈[90,100],则有 ab、bc、ac 三种情况,..............6 分
若 m、n 分别在[50,60)和[90,100]内,则有
a b c
x xa xb xc 共 6 种情况.
y ya yb yc..............8 分
所以基本事件总数为 10 种,事件“|m-n|>10”所包含的基本事件有 6 种,.......9 分
∴P(|m-n|>10)= 6
10=3
5...............10 分
18.解(1)由题意可知 p=2。……2 分∴抛物线标准方程为:x2=4y…………5 分
(2)直线 l:y=2x+l 过抛物线的焦点 ,设
联立 得 x2-8x-4=0………………8 分
∴x1+x2=8……………10 分
∴ ……………12 分
19.[解析] (1)∵f(x)=ax3+bx+c,∴f ′(x)=3ax2+b,..............1 分
∵f(x)在点 x=2 处取得极值 c-16,
∴Error!即Error!..............3 分
化简得Error!解得Error!..............5 分
(2)由(1)知 f(x)=x3-12x+c,f ′(x)=3x2-12,
令 f ′(x)=0,得 x1=-2,x2=2,
当 x∈(-∞,-2)时,f ′(x)>0,f(x)在(-∞,-2)上为增函数,..............6 分
当 x∈(-2,2)时,f ′(x)<0,f(x)在(-2,2)上为减函数,..............7 分
1,sin 00 >∈ xRx
6
1
)1,0(F ),(),( 2211 yxByxA ,
=
+=
yx
xy
4
12
2
204)(2212122 212121 =++=++++=++= xxxxyyAB
当 x∈(2,+∞)时 f ′(x)>0,f(x)在(2,+∞)上为增函数..............8 分
故 f(x)在 x1=-2 处取得极大值 f(-2)=16+c,f(x)在 x2=2 处取得极小值 f(2)=c-16,
由题设条件知 16+c=28 得 c=12,..............10 分
此时 f(-3)=9+c=21,f(3)=-9+c=3,f(2)=c-16=-4,
因此 f(x)上[-3,3]的最小值为 f(2)=-4. ..............12 分
20. (1) 证明:取 AB 中点 E,连结 CE, , ,
∵AB= , = ,∴ 是正三角形,
∴ ⊥AB,
∵CA=CB, ∴CE⊥AB,
∵ =E,∴AB⊥面 ,
∴AB⊥ ; ..............5 分
(2)由(Ⅰ)知 EC⊥AB, ⊥AB,
又∵面 ABC ⊥面 , 面 ABC∩ 面 =AB,
∴EC ⊥面 , ∴EC ⊥ , ..............6 分
∴EA,EC, 两两相互垂直,以 E 为坐标原点, 的方向为 轴正方向,| |为单位长
度,建立如图所示空间直角坐标系 , ..............7 分
有题设知 A(1,0,0), (0, ,0),C(0,0, ),B(-1,0,0),则 =(1,0, ), = =(-1,0,
), =(0,- , ), ..............8 分
设 = 是平面 的法向量,
则 ,即 ,可取 =( ,1,-1), ..............9 分
∴ = , ..............11 分
∴直线 A1C 与平面 BB1C1C 所成角的正弦值为 .............12 分
1A B 1A E
1AA 1BAA∠ 060 1BAA∆
1A E
1CE A E∩ 1CEA
1AC
1EA
1 1ABB A 1 1ABB A
1 1ABB A 1EA
1EA EA x EA
O xyz−
1A 3 3 BC 3 1BB
1AA
3 1AC 3 3
n ( , , )x y z 1 1CBB C
1
0
0
BC
BB
• = • =
n
n
3 0
3 0
x z
x y
+ =
+ =
n 3
1cos , ACn 1
1 |
AC
AC
•
n
| n ||
10
5
10
5
x
y
C
B
NM
T
O
A
21. (12 分) 解: (I) 直线 的斜率为 1.函数 的定义域为 ,
∵ , ∴ , ∴ . ∴ .
.由 解得 ;由 解得 .
∴ 的单调增区间是 ,单调减区间是 . ..............5 分
(II) ,由 解得 ;由 解得 .
∴ 在区间 上单调递增,在区间 上单调递减. ..............7 分
∴当 时,函数 取得最小值, ...............8 分
∵对于 都有 成立,∴ 即可. ..............10 分
则 . 由 解得 .∴ 的取值范围是 .
.............12 分
22.(本小题满分 12 分)
【解析】(Ⅰ)设圆 的半径为 ( ),依题意,圆
心坐标为 . ..............1 分
∵
∴ ,解得 ............................3 分
∴ 圆 的方程为 ...............5 分
(Ⅱ)把 代入方程 ,解得 ,或 ,
即点 , . ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6 分
(1)当 轴时,由椭圆对称性可知 . ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7 分
(2)当 与 轴不垂直时,可设直线 的方程为 .
联立方程 ,消去 得, .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8 分
设直线 交椭圆 于 两点,则
, . ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9 分
∵ ,
∴
2y x= + ( )f x (0, )+∞
2
2( ) af x x x
′ = − + 2
2(1) 11 1
af ′ = − + = − 1a = 2( ) ln 2f x xx
= + −
2
2( ) xf x x
−′ = ( ) 0f x′ > 2x > ( ) 0f x′ < 0 2x< <
( )f x (2, )+∞ (0,2)
2 2
2 2( ) a axf x x x x
−′ = − + = ( ) 0f x′ > 2x a
> ( ) 0f x′ < 20 x a
< <
( )f x 2( , )a
+ ∞ 2(0, )a
2x a
= ( )f x min
2( )y f a
=
(0, )x∀ ∈ +∞ ( ) 2( 1)f x a> − 2( ) 2( 1)f aa
> −
2 2ln 2 2( 1)2 a aa
a
+ − > − 2lna aa
> 20 a e
< < a 2(0, )e
C r 0r >
( ,2)r
3MN =
2
2 23 22r = +
2 25
4r =
C ( )2
25 2522 4x y − + − =
0y = ( )2
25 2522 4x y − + − = 1x = 4x =
( )1,0M ( )4,0N
AB x⊥ ANM BNM∠ = ∠
AB x AB ( )1y k x= −
( )
2 2
1
2 8
y k x
x y
= −
+ =
y ( )2 2 2 22 2 8 0k x k x k+ − + − =
AB Γ ( ) ( )1 1 2 2, ,A x y B x y、
2
1 2 2
2
2
kx x k
+ = +
2
1 2 2
8
2
kx x k
−⋅ = +
( ) ( )1 1 2 22 , 2y k x y k x= − = −
( ) ( )1 21 2
1 2 1 2
1 1
4 4 4 4AN BN
k x k xy yk k x x x x
− −+ = + = +− − − −
第 22 题图
. ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10 分
∵ ,
∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11 分
∴ , .
综上所述, .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12 分
( )( ) ( )( )
( )( )
1 2 2 1
1 2
1 4 1 4
4 4
k x x k x x
x x
− − + − −= − −
( )( ) ( )( ) ( ) ( )2 2
1 2 2 1 1 2 1 2 2 2
2 8 101 4 1 4 2 5 8 8 02 2
k kx x x x x x x x k k
−
− − + − − = − + + = − + =+ +
0AN BNk k+ = ANM BNM∠ = ∠
ANM BNM∠ = ∠