- 2022-09-27 发布 |
- 37.5 KB |
- 9页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
理论力学静力学与运动学部分复习题及答案
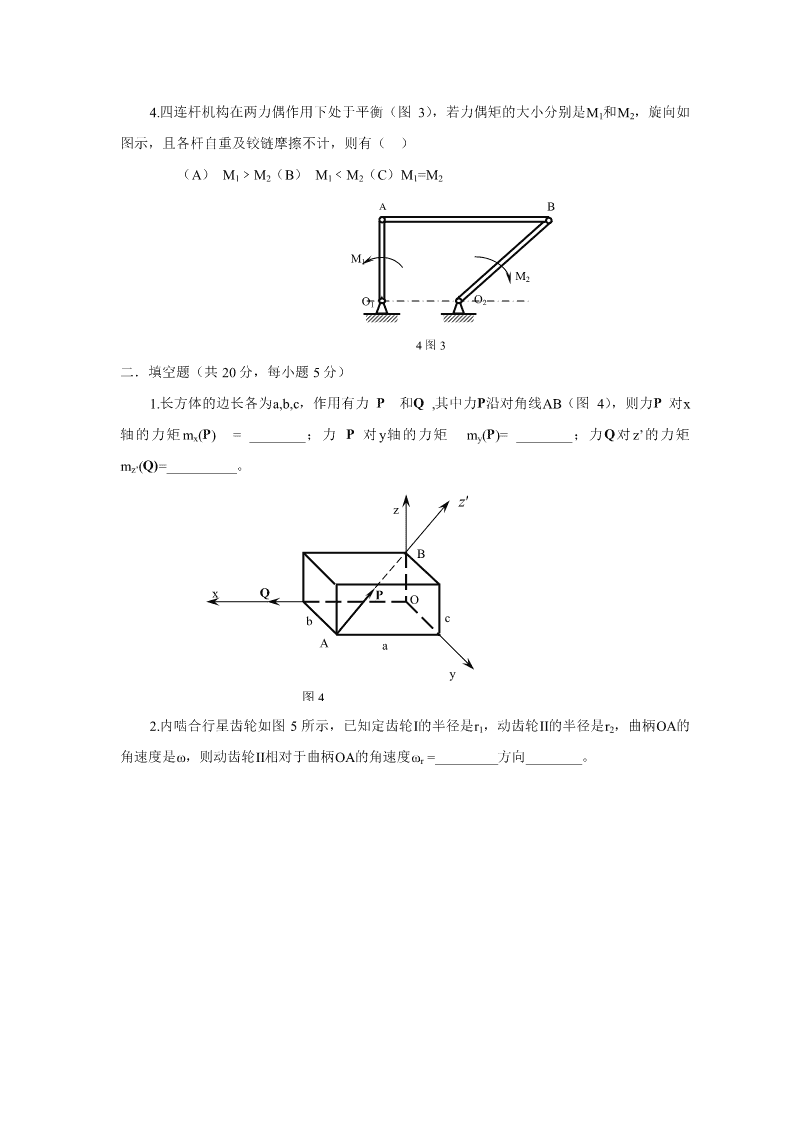
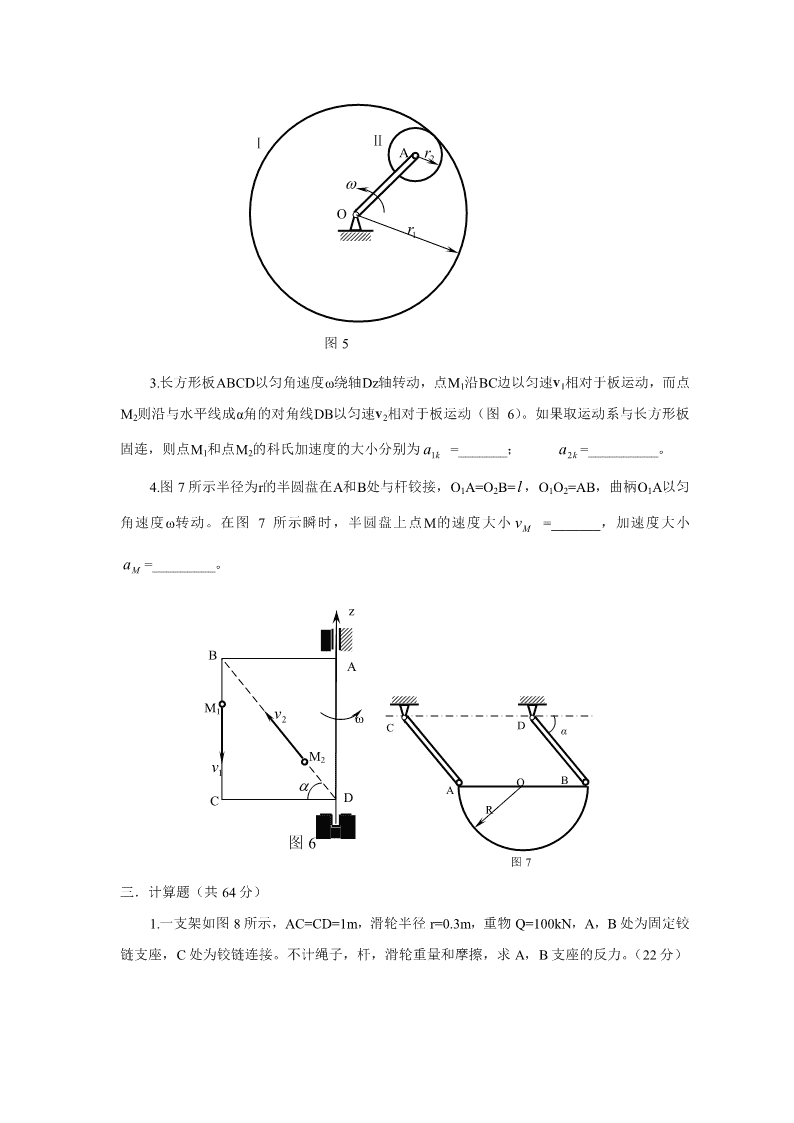
理论力学试题(静力学与运动学部分)一.选择题(把正确答案的序号填入括号内,共16分,每小题4分)1.不平衡的空间平行力系合成的最后结果()。(A)只能是一个力(B)只能是一个力或一个力偶(C)只能是一个力或一个力螺旋(D)只能是一个力偶或一个力螺旋2.一平面任意力系向点A简化后,得到如图1所示的主矢R’和主矩LA,则该力系的最后合成结果应是()(A)作用在点A左边的一个合力(B)作用在点A右边的一个合力(C)作用在点A的一个合力(D)一个合力偶3.重2000N的物块静止放在倾角α=30°的斜面上,力P平行于斜面并指向上方,其大小等于100N(图2)。已知物块和斜面间的静摩擦因数f=0.3,则斜面对物块的摩擦力的大小等于()(A)1003×0.3N(B)100N(C)0(D)100(1−3×0.3)NAPLAR'α图1图2\n4.四连杆机构在两力偶作用下处于平衡(图3),若力偶矩的大小分别是M1和M2,旋向如图示,且各杆自重及铰链摩擦不计,则有()(A)M1﹥M2(B)M1﹤M2(C)M1=M2ABM1M2O1O24图3二.填空题(共20分,每小题5分)1.长方体的边长各为a,b,c,作用有力P和Q,其中力P沿对角线AB(图4),则力P对x轴的力矩mx(P)=________;力P对y轴的力矩my(P)=________;力Q对z’的力矩mz’(Q)=__________。z'zBxQPObcAay图42.内啮合行星齿轮如图5所示,已知定齿轮I的半径是r1,动齿轮II的半径是r2,曲柄OA的角速度是ω,则动齿轮II相对于曲柄OA的角速度ωr=_________方向________。\nⅠⅡAr2ωOr1图53.长方形板ABCD以匀角速度ω绕轴Dz轴转动,点M1沿BC边以匀速v1相对于板运动,而点M2则沿与水平线成α角的对角线DB以匀速v2相对于板运动(图6)。如果取运动系与长方形板固连,则点M1和点M2的科氏加速度的大小分别为a1k=_______;a2k=__________。4.图7所示半径为r的半圆盘在A和B处与杆铰接,O1A=O2B=l,O1O2=AB,曲柄O1A以匀角速度ω转动。在图7所示瞬时,半圆盘上点M的速度大小v=_______,加速度大小Ma=_________。MzBAM1vω2CDαM2v1αOBACDR图6图7三.计算题(共64分)1.一支架如图8所示,AC=CD=1m,滑轮半径r=0.3m,重物Q=100kN,A,B处为固定铰链支座,C处为铰链连接。不计绳子,杆,滑轮重量和摩擦,求A,B支座的反力。(22分)\nEAC1mBHQ图82.半径R=20cm的圆轮,在水平直线轨道上作纯滚动,杆AB的A端与圆轮边缘上的点A铰接,2B端与杆OB在点B铰接,在图示位置时,轮心C的速度vC=60cm/s,加速度aM=60cm/s,方向如图9所示。试求:杆OB的角速度和点A的加速度大小。(cos75°=0.2588)(18分)BRvacc30°2RCAO图92.在图10所示的平面机构中,曲柄长为r,以匀角速度ω沿逆时针转动,杆OA和AB,AB和BE分别在A,B铰接,AB=BE=l,杆CD与套筒C铰接,套筒V可沿杆BE滑动,在图示瞬时,AB⊥BE,OA⊥OB,BC=CE,试求:该瞬时杆BE的角速度和角加速度,以及杆CD沿水平导槽滑动的速度。(24分)E30°ACDrω30°OB(a)速度分析\nE30°ACDrω30°OB(b)加速度分析图10自测题四解答一.选择题1.(B)2.(A)3.(C)4.(C)二.填空题1.解⑴取整体为研究对象(图1(a))∑mA(F)=NBX×1−Q×2.3=0⑴所以N=230kNBx∑mB(F)=−NAX×1−Q×2.3=0⑵所以N=−230kNAx∑Fy=NAy+NBy−Q=0⑶yENAyANAxCDNByHQBxNBx(a)\nyTNCyNAyADNAxCNCxQ(b)图1⑵取AD杆及滑轮为研究对象(图1(b))∑mC(F)=−NAy×1−Q×1.3+T×0.3=0⑷所以N=−100NAy将N带入方程⑶,得N=Q−N=200kNAyByAy从而有N=−230kN,N=−100NAxAyN=230kN,N=200kNBxBy2.解:vc⑴求杆OB的角速度ω(图2(a)),圆轮作平面运动,其角速度ω=。杆OBOBR作定轴转动,设其角速度为ω。杆AB作平面运动。根据速度投影法,有OB[v]=[v]⑴BABAABv=OB•ω=2R•ω,v=2Rω=2vBOBOBAC则有vcos30°=vcos75°BA2vcos75°C所以ω==25.35rad/sOBcos30°⑵求点A的加速度(图2(b)),取圆轮中心点C为基点,则点A的加速度为τna=a+a+a⑵ACACAC式中各参数为加速度aaaτanACACAC\n大小未知aRε(ε=a/R)Rω2CC方向未知←↑←故有2n2τ260222a=(a+a)+(a)=(20+)+20=201.0cm/sAcACAC20ωvBBvAvc45°θ2RCAωOBRO(a)τBεaACaCaCθωCanAACO(b)图23.解⑴求杆BE的角速度和角加速度,杆OA绕轴O作定轴转动,角速度为ω,故杆OA,A端速度大小为v=BE•ω(图3(a))。杆AB作平面运动,根据速度投影法,有BBE[v]=[v]⑴BABAAB则有v=vcos30°BA又vB=vA+vBA,vBA=vAsin30°vBArω所以ω==ABAB2l由基点法(图3(b))τna=a+a+a⑵BABABA\nτn又a=a+a⑶BBB由式(2)和(3),有τnτna+a=a+a+a⑷BBABABA将式(4)投影到x’轴上,有τna=a−acos60°BBAAn2而a=AB•ωBAABrω21232a=l()−rω=−rωA2l28所以vBrωcos30°3rω3ω====ωBEBEl2l4τ22aB3rω3ωε==−=−BEBE8l16Ev30°CvCAADvCrvBvCωvBA30°OBvA(a)E΄x30°CADranBAτaAaBAωτaBnaB30OBaa(b)图3⑵求杆CD的滑动速度(图3(a))v=v+v⑸CCeCr\nvEC•ωCeBEv==Csin60°sin60°l3211所以v=×ω×=lω=rωC24342查看更多