- 2022-09-27 发布 |
- 37.5 KB |
- 25页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
电力拖动自动控制系统—运动控制系统(第四版)习题答案
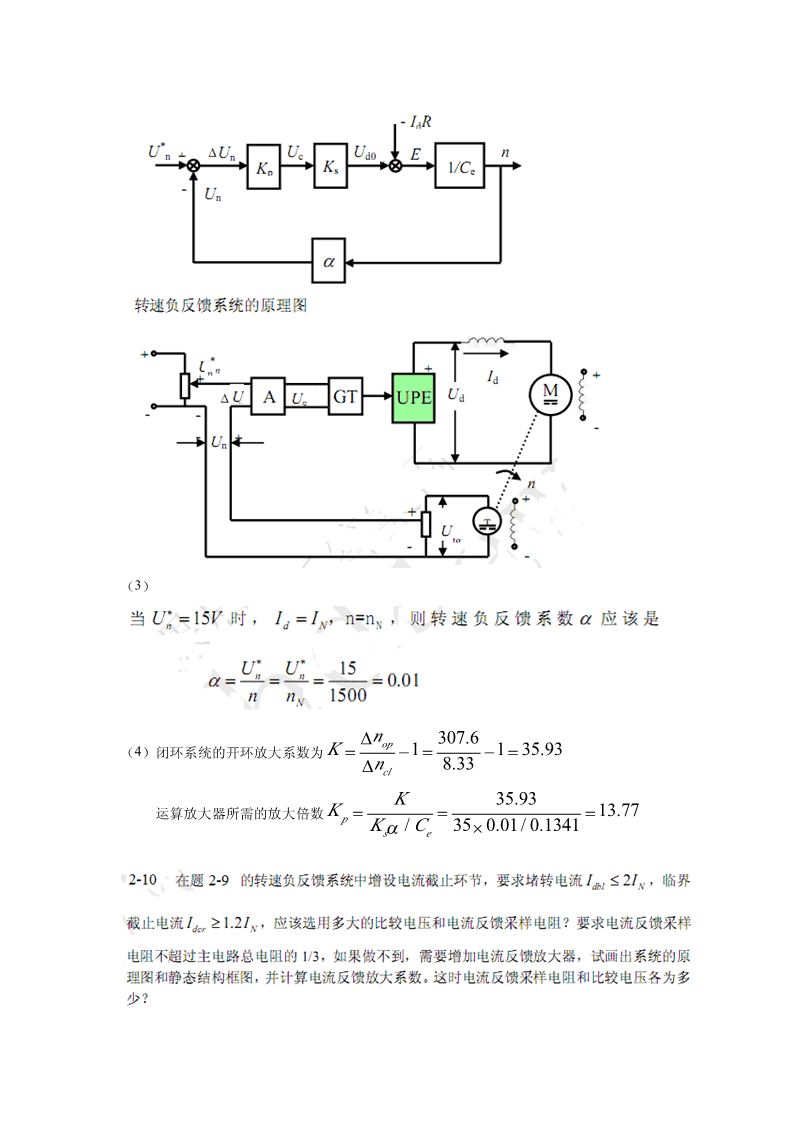
《电力拖动自动控制系统—运动控制系统》习题2-2调速系统的调速范围是1000~100r/min,要求静差率s=2%,那么系统允许的稳态速降是多少?解:系统允许的稳态速降sn0.02×100min∆n===2.04(rmin)N(1−s)(1−0.02)2-5某龙门刨床工作台采用晶闸管整流器-电动机调速系统。已知直流电动机P=60kW,NU=220V,I=305A,n=1000rmin,主电路总电阻R=0.18Ω,NNNC=0.2V•minr,求:e(1)当电流连续时,在额定负载下的转速降落∆n为多少?N(2)开环系统机械特性连续段在额定转速时的静差率s多少?N(3)额定负载下的转速降落∆n为多少,才能满足D=20,s≤5%的要求。N解:(1)当电流连续时,在额定负载下的转速降落INR305×0.18∆n===274.5(rmin)NC0.2e(2)开环系统机械特性连续段在额定转速时的静差率∆nN274.5s==≈0.215=21.5%Nn+∆n1000+274.5NN(3)额定负载下满足D=20,s≤5%要求的转速降落ns1000×0.05N∆n==≈2.63(rmin)ND(1−s)20×(1−0.05)*2-6有一晶闸管稳压电源,其稳态结构如图所示,已知给定电压U=8.8V,比例调节放大u系数K=2,晶闸管装置放大系数K=15,反馈系数γ=0.7。求:ps(1)输出电压U;d(2)若把反馈线断开,U为何值?开环时的输出电压是闭环时的多少倍?d*(3)若把反馈系数减至γ=0.35,当保持同样的输出电压时,给定电压U应为多少?u解:(1)输出电压KpKs*2×15U=U=×8.8=12(V);du1+KKγ1+2×15×0.7ps*(2)若把反馈线断开,U=KKU=2×15×8.8=264(V);开环时的输出电压是闭环dpsu时的26412=22倍。(3)若把反馈系数减至γ=0.35,当保持同样的输出电压时,给定电压*1+KpKsγ1+2×15×0.35U=U=×12=4.6(V)。udKK2×15ps\nU−IR22012.51.5−×解:(1)NdaC===0.1341V⋅min/ren1500NRI12.5(1.51.00.8)×++N∆n===307.6/minropC0.1341ens15000.1×N∆n=≤=8.33/minrclD(1−s)20(10.1)×−(2)\n(3)∆nop307.6(4)闭环系统的开环放大系数为K=−=1−=135.93∆n8.33clK35.93运算放大器所需的放大倍数K===13.77pKα/C350.01/0.1341×se\n解:R=4.8ΩRs/R=0.31251/3<图见49页解:计算系统中各环节的时间常数L0.05电磁时间常数T===0.02slR1.51.0+2GDR1.6(1.51.00.8)×++机电时间常数T===0.082sm375CC30em3750.1341×××0.1341π晶闸管装置的滞后时间常数为T=0.00167ss为保证系统稳定,应满足的稳定条件:22TT(+T)+T0.082(0.020.00167)0.00167×++mlssK<==53.29TT0.020.00167×ls可以稳定运行,最大开环放大系数是53.292-12有一晶闸管-电动机调速系统,已知:电动机P=2.8kW,U=220V,I=15.6A,NNNn=1500rmin,R=1.5Ω,整流装置内阻R=1Ω,电枢回路电抗器电阻R=0.8Ω,NarecL触发整流环节的放大倍数K=35。求:s(1)系统开环时,试计算调速范围D=30时的静差率s。\n(2)当D=30,s=10%时,计算系统允许的稳态速降。*(3)如组成转速负反馈有静差调速系统,要求D=30,s=10%,在U=10V时I=I,ndNn=n,计算转速反馈系数α和放大器放大系数K。Np解:先计算电动机的反电动势系数U−IR220−15.6×1.5NNaC===0.131(V•minr)en1500N系统开环时的额定转速降落I(R+R+R)15.6×(1.5+1+0.8)NarecL∆n==≈393(rmin)NopC0.131e(1)系统开环时,调速范围D=30时的静差率D∆nN30×393s==≈0.887=88.7%;n+D∆n1500+30×393NN(2)当D=30,s=10%时,系统允许的稳态速降nNs1500×0.1∆n==≈5.56(rmin)ND(1−s)30×(1−0.1)(3)如组成转速负反馈有静差调速系统,要求D=30,s=10%,则系统开环放大系数∆nop393K=−1=−1≈69.68;∆n5.56cl*Un10转速反馈系数α==≈0.0067(V•minr)n1500NKCe69.68×0.131放大器放大系数K==≈38.93。pKα35×0.0067s2-13旋转编码器光栅数为1024,倍数系数为4,高频时时钟脉冲频率f=1MHz,旋转编0码器输出的脉冲个数和高频时钟脉冲个数均采用16位计算器,M法和T法测速时间均为0.01s,求转速n=1500r/min和n=150r/min时的测速分辨率和误差率最大值。解:(1)M法测速6060转速n=1500r/min和n=150r/min时的测速分辨率Q==≈1.465ZT1024×4×0.01cnZT1500×4096×0.01c转速n=1500r/min时,M===1024,误差率最大值1606011δ==≈0.00097=0.097%;maxM10241nZT150×4096×0.01c转速n=150r/min时,M===102.4,误差率最大值1606011δ==≈0.0097=0.97%。maxM102.41(2)T法测速660f60×1×100转速n=1500r/min时,M==≈9.8,测速分辨率2Zn4096×150022Zn4096×1500Q==≈171660f−Zn60×1×10−4096×15000\n误差率最大值11δ==≈0.103=10.3%。maxM−19.8−12660f60×1×100转速n=150r/min时,M==≈98,测速分辨率2Zn4096×15022Zn4096×150Q==≈1.55660f−Zn60×1×10−4096×1500误差率最大值11δ==≈0.0103=1.03%。maxM−198−123-1双闭环直流调速系统的ASR和ACR均为PI调节器,设系统最大给定电压**U=U=15V,n=1500rmin,I=20A,电流过载倍数为2,电枢回路总电阻nmimNNR=2Ω,K=20,C=0.127V⋅minr,求:se**(1)当系统稳定运行在U=5V,I=10A时,系统的n、U、U、U和U各为多少?ndLniic*(2)当电动机负载过大而堵转时,U和U各为多少?ic解:转速反馈系数*Unm15α===0.01(V⋅minr)n1500N电流反馈系数*Uim15β===0.375(VA)I2×20dm*(1)当系统稳定运行在U=5V,I=10A时,ndL*U=U=5(V)nn*U5nn===500(rmin)α0.01U=βI=0.375×10=3.75(V)idL*U=U=3.75(V)iiUd0Cen+IdLR0.127×500+10×2U====4.175(V)。cKK20ss(2)当电动机负载过大而堵转时,n=0;*U=βI=0.375×2×20=15(V)idmIdmR2×20×2U===4(V)。cK20s3-2在转速、电流双闭环直流调速系统中,两个调节器ASR、ACR均采用PI调节器。已知参数:电动机:P=3.7kW,U=220V,I=20A,n=1000rmin,电枢回路NNNN**总电阻R=1.5Ω;设U=U=U=8V,电枢回路最大电流I=40A,电力电子变nmimcmdm换器的放大倍数K=40。试求:s(1)电流反馈系数β和转速反馈系数α;*(2)当电动机在最高转速发生堵转时的U,U,U和U的值。d0iic\n解:(1)电流反馈系数*Uim8β===0.2(VA)I40dm转速反馈系数*Unm8α===0.008(V⋅minr)。n1000N(2)当电动机在最高转速发生堵转时,n=0;U=Cn+IR=0+40×1.5=60(V)d0edm*U=U=βI=0.2×40=8(V)iidmUd060U===1.5(V)。cK40s3-5某反馈系统已校正成典型I型系统。已知时间常数T=0.1s,要求阶跃响应超调量σ≤10%。(1)系统的开环增益。(2)计算过渡过程时间t和上升时间t。sr(3)绘出开环对数幅频特性。如果要求上升时间t<0.25s,则K=?σ=?r解:典型I型系统开环传递函数为KW(s)=s(Ts+1)(1)要求阶跃响应超调量σ≤10%,则要求KT≤0.69,为获得尽量短的上升时间t,选r择KT=0.69;则K=0.690.1=6.9(2)过渡过程时间t=6T=6×0.1=0.6(s);s上升时间t=3.3T=3.3×0.1=0.33(s)。r(3)如果要求上升时间t<0.25s,则选择KT=1;rK=10.1=10,σ=16.3%。K(τs+1)解:PI调节器iiW(s)=τsi10Ki(τs+1)i10K(τs+1)τ开环传递函数iiiW()s=⋅=op2s(0.02s+1)τss(0.02s+1)i对Ⅱ型系统σ≤30%,h=7τ=hT=0.14si\nh+1K==204.1222hTKτiK==2.8571i102.8571(0.14s+1)PI调节器W()s=0.14sRiK=R取10kΩR=28.571kΩ取30kΩi0iR0C=R/τ=14µFiii\n\n\n∆Cmax∆nNT∑n4h=3σ%=2(%)(λ−z)=63.4%n*CnTbm3-10有一转速、电流双闭环直流调速系统,主电路采用三相桥式整流电路。已知电动机参数为:P=500kW,U=750V,I=760A,n=375rmin,电动势系数NNNNC=1.82V⋅minr,电枢回路总电阻R=0.14Ω,允许电流过载倍数λ=1.5,触发整流e环节的放大倍数K=75,电磁时间常数T=0.031s,机电时间常数T=0.112s,电流反slm馈滤波时间常数T=0.002s,转速反馈滤波时间常数T=0.02s。设调节器输入输出电oion**压U=U=U=10V,调节器输入电阻R=40kΩ。nmimnm0设计指标:稳态无静差,电流超调量σ≤5%,空载起动到额定转速时的转速超调量iσ≤10%。电流调节器已按典型I型系统设计,并取参数KT=0.5。n(1)选择转速调节器结构,并计算其参数。(2)计算电流环的截止频率ω和转速环的截止频率ω,并考虑它们是否合理?cicn解:三相桥式整流电路的平均失控时间T=0.0017s,电流环小时间常数之和sT=T+T=0.0037s,要求电流超调量σ≤5%,应取KT=0.5,因此ΣisoiiIΣi−1K≈135.1s。I(1)电流环等效时间常数1K=0.0074s;I转速环小时间常数T=1K+T=0.0074+0.02=0.0274s;ΣnIon电流反馈系数\n*Uim10β==≈0.0088(VA)λI1.5×760N转速反馈系数*Unm10α===0.0267(V⋅minr)n375N选择转速调节器结构,其传递函数为K(τs+1)nnW(s)=ASRτsn按跟随和抗扰动性能都较好的原则,取h=5,则ASR的超前时间常数为τ=hT=5×0.0274=0.137snΣn转速环开环增益h+15+1−2K===159.84s,N22222hT2×5×0.0274Σn可得ASR的比例系数为(h+1)βCeTm6×0.0088×1.82×0.112K==≈10.51;n2hαRT2×5×0.0267×0.14×0.0274Σn取调节器输入电阻R=40kΩ,则0R=KR=10.51×40=420.4kΩ,取420kΩnn0τn0.137−7C===3.26×10(F)=0.326µF,取0.33µFn3R420×10n4Ton4×0.02−6C===2×10(F)=2µF,取2µF。on3R40×100−1(2)电流环的截止频率ω=K=135.1s,ciI−1转速环的截止频率ω=Kτ=159.84×0.137≈21.9s;cnNn检验近似条件1)校验晶闸管整流装置传递函数的近似条件11−1=≈196.1(s)>ω,满足近似条件;ci3T3×0.0017s校验忽略反电动势变化对电流环动态影响的条件11−13=3≈50.91(s)<ω,满足近似条件;ciTT0.112×0.031ml校验电流环小时间常数近似条件1111−1=≈180.8(s)>ω,满足近似条件;ci3TT30.0017×0.002soi校验电流环传递函数近似条件1KI1135.1−1=≈63.7(s)>ω,满足近似条件;cn3T30.0037Σi校验转速环小时间常数近似条件1KI1135.1−1=≈27.4(s)>ω,满足近似条件。cn3T30.02on校核转速超调量\n⎛∆C⎞∆n⎜max⎟bσ=n⎜C⎟n*⎝b⎠⎛∆C⎞∆nT⎜max⎟NΣn=2(λ−z)⎜⎟*⎝Cb⎠nTm760×0.141.820.0274=2×0.812×(1.5−0)××3750.112≈0.093<10%满足设计要求。\n15解:(1)α==0.01V⋅min/r1500*U5nn===500/minrα0.01U=Cn+IR=104Vd0edUd0U==3.47VcKs(2)当电动机突然失磁,电机停转。U=0n**U=U=10ViimU=−10ViI=I=2VddmKs(τ+1)(3)Ws()=2sTs(+1)τ=hT=0.25sh+1−2K==48sN222hT48(0.25s+1)Ws()=2s(0.05s+1)(4)t=8.8T=0.44svm\n2RT(I−I)∑ndmdL∆n==93.75/minrbCTem∆Cmax∆n=(%)∆n=76.12/minrmaxbCb5-1一台三相鼠笼异步电动机的铭牌数据为:额定电压U=380V,额定转速Nn=960rmin,额定频率f=50Hz,定子绕组为Y联接。由实验测得定子电阻NNR=0.35Ω,定子漏感L=0.006H,定子绕组产生气隙主磁通的等效电感L=0.26H,slsm转子电阻R′=0.5Ω,转子漏感L′=0.007H,转子参数已折算到定子侧,忽略铁芯损耗。rlr(1)画出异步电动机T形等效电路和简化电路。(2)额定运行时的转差率s,定子额定电流I和额定电磁转矩。N1N(3)定子电压和频率均为额定值时,理想空载时的励磁电流I。0(4)定子电压和频率均为额定值时,临界转差率s和临界转矩T,画出异步电动机的机mem械特性。解:(1)异步电动机T形等效电路异步电动机简化电路60f60×50N(2)由于额定转速n=960rmin,同步转速n===1000(rmin),N1n3pn−n1000−960额定运行时的转差率s=1==0.04Nn10001由异步电动机T形等效电路,R+jωLLR0.0060.35s1lslssC=1+=1+−j=1+−j≈1.023−j0.004≈1.0231jωLL2πfL0.26100π×0.261mmNm可得转子相电流幅值\nUsI′=r2⎛Rr′⎞22⎜R+C⎟+ω(L+CL′)⎜s1s⎟1ls1lr⎝N⎠220=2⎛0.5⎞2()2⎜0.35+1.023×⎟+(100π)×0.006+1.023×0.007⎝0.04⎠220=172.5939+17.0953=15.9735(A)气隙磁通在定子每相绕组中的感应电动势2⎛Rr′⎞22E=I′⎜⎟+ωL′=15.9735×156.25+4.8361≈202.7352(V)gr⎜s⎟1lr⎝N⎠额定运行时的励磁电流幅值Eg202.7352I==≈2.482(A)0ωL100π×0.261m由异步电动机简化电路,额定运行时的定子额定电流幅值U220sI==1N22⎛R2′⎞22⎛0.5⎞22⎜Rs+⎟+ω1(Lls+Llr′)⎜0.35+⎟+(100π)×(0.006+0.007)⎝s⎠⎝0.04⎠220=165.1225+16.6796=16.3164(A)额定电磁转矩=Pm=3np′2Rr′3×320.5TI=×15.9735×≈91.37(N⋅m)(依据T形等效电路)erωωs100π0.04m1N或Pm3np2Rr′3×320.5T==I=×16.3164×≈95.33(N⋅m)(依据简化等效电路)e1Nωωs100π0.04m1N(3)定子电压和频率均为额定值时,理想空载时的励磁电流U220sI===2.633(A)02ω2()20.352+(100π)2×(0.006+0.26)2R+L+Ls1lsm(4)定子电压和频率均为额定值时,临界转差率R′0.5rs===0.122m2ω220.352+(100π)2×(0.006+0.007)2R+(L+L′)s1lslr临界转矩223npUs3×3×220T==emω⎡2ω22⎤200×π×0.35+0.352+(100π)2×(0.006+0.007)22R+R+(L+L′)[]1⎢⎣ss1lslr⎥⎦=155.83(N⋅m)\n异步电动机的机械特性:Sn0n1Sm10TTeme125-2异步电动机参数如习题5-1所示,画出调压调速在U和U时的机械特性,计算临NN23界转差率s和临界转矩T,分析气隙磁通的变化,在额定电流下的电磁转矩,分析在恒转mem矩负载和风机类负载两种情况下,调压调速的稳定运行范围。解:定子相电压改变,临界转差率不变,即R′0.5rs===0.122m2ω220.352+(100π)2×(0.006+0.007)2R+(L+L′)s1lslr111当调压至U时,临界转矩T=T=×155.83=38.96(N⋅min),Nememax244244当调压至U时,临界转矩T=T=×155.83=69.26(N⋅min)。Nememax399U气隙磁通:Φ≈s随定子电压的降低而减小。m4.44fNk1sNs5-6异步电动机参数如习题5-1所示,输出频率f等于额定频率fN时,输出电压U等于额定电压UN,考虑低频补偿,若频率f=0,输出电压U=10%UN。(1)求出基频以下电压频率特性曲线U=f(f)的表达式,并画出特性曲线。(2)当f=5Hz和f=2Hz时,比较补偿与不补偿的机械特性曲线,两种情况下的临界转矩Temax。解:(1)UN=220(A)斜率\nU−0.1U220−22k=NN==3.96,f−050−0N考虑低频补偿时,电压频率特性曲线U=3.96f+22;220不补偿时,电压频率特性曲线U=f=4.4f50(2)当f=5Hz时A、不补偿时,输出电压U=4.4f=22(V),临界转矩3nU22ps3×3×22Tem==ω⎡2ω22⎤20×π×0.35+0.352+(10π)2×(0.006+0.007)22R+R+(L+L′)[]1⎢⎣ss1lslr⎥⎦=78.084(N⋅m)B、补偿时,输出电压U=3.96f+22=41.8(V)3nU22ps3×3×41.8Tem==ω⎡2ω22⎤20×π×0.35+0.352+(10π)2×(0.006+0.007)22R+R+(L+L′)[]1⎢⎣ss1lslr⎥⎦=281.883(N⋅m)当f=2Hz时A、不补偿时,输出电压U=4.4f=8.8(V),临界转矩3nU22ps3×3×8.8Tem==ω⎡2ω22⎤8×π×0.35+0.352+(4π)2×(0.006+0.007)22R+R+(L+L′)[]1⎢⎣ss1lslr⎥⎦=37.666(N⋅m)B、补偿时,输出电压U=3.96f+22=29.92(V)3nU22ps3×3×29.92Tem==ω⎡2ω22⎤8×π×0.35+0.352+(4π)2×(0.006+0.007)22R+R+(L+L′)[]1⎢⎣ss1lslr⎥⎦=435.419(N⋅m)5-8两电平PWM逆变器主回路,采用双极性调制时,用“1“表示上桥臂开通,”0“表示上桥臂关断,共有几种开关状态,写出其开关函数。根据开关状态写出其电压矢量表达式,画出空间电压矢量图。解:\n\n5-11采用电压空间矢量PWM调制方法,若直流电压u恒定,如何协调输出电压与输出频d率的关系。解:在一个周期内,6个有效工作矢量顺序作用一次,定子磁链矢量是一个封闭的正六边形。22πudψ(k)=∆ψ(k)=u(k)∆t=u∆t=ssd333ω1正六边形定子磁链的大小与直流侧电压成正比,而与电源角频率成反比。在基频以下调速时,应保持正六边形定子磁链的最大值恒定。若直流侧电压恒定,则ω越小时,∆t越大,势必1导致ψ(k)增加。因此,要保持正六边形定子磁链不变,必须使uω为常数,这意味着sd1在变频的同时必须调节直流电压,造成了控制的复杂性。有效的方法是插入零矢量,当零矢量作用时,定子磁链矢量的增量∆ψ(k)=0,表明s定子磁链矢量停留不动。有效工作矢量作用时间∆t<∆t,1零矢量作用时间∆t=∆t−∆t,01当ω∆t=ω(∆t+∆t)=π3时,定子磁链矢量的增量为1110正六边形定子磁链的最大值在直流电压不变的条件下,要保持ψ(k)恒定,只要使∆t为常数即可。输出频率越低,∆ts1越大,零矢量作用时间∆t也越大,定子磁链矢量轨迹停留的时间越长。由此可知,零矢量0\n的插入有效地解决了定子磁链矢量幅值与旋转速度的矛盾。6-1按磁动势等效、功率相等原则,三相坐标系变换到两相静止坐标系的变换矩阵为⎡11⎤1−−2⎢22⎥C32=⎢⎥333⎢0−⎥⎢⎣22⎥⎦2π2π现有三相正弦对称电流i=Isin(ωt)、i=Isin(ωt−)、i=Isin(ωt+),求AmBmCm33变换后两相静止坐标系中的电流i和i,分析两相电流的基本特征与三相电流的关系。sαsβ⎡⎤⎡11⎤⎢Imsin(ωt)⎥⎡i⎤2⎢1−−⎥⎢2π⎥3⎡Isin(ωt)⎤sα22m解:⎢⎥=⎢⎥⎢Imsin(ωt−)⎥=⎢⎥;⎣isβ⎦3⎢03−3⎥⎢3⎥2⎣−Imcos(ωt)⎦⎢⎣22⎥⎦⎢Isin(ωt+2π)⎥m⎢⎣3⎥⎦6-2两相静止坐标系到两相旋转坐标系的变换矩阵为⎡cosϕsinϕ⎤C=2s2r⎢⎥⎣−sinϕcosϕ⎦将习题6-1中的静止坐标系中的电流i和i变换到两相旋转坐标系中的电流i和i,坐sαsβsdsqdϕ标系旋转速度为=ω。分析当ω=ω时,电流i和i的基本特征,电流矢量幅值11sdsqdt22i=i+i与三相电流幅值I的关系,其中ω是三相电源角频率。ω>ω和ω<ω时,ssdsqm11i和i的表现形式。sdsq⎡isd⎤⎡cosϕsinϕ⎤3⎡Imsin(ωt)⎤3⎡Imsin(ωt−ϕ)⎤解:⎢⎥=⎢⎥⎢⎥=⎢⎥⎣isq⎦⎣−sinϕcosϕ⎦2⎣−Imcos(ωt)⎦2⎣−Imcos(ωt−ϕ)⎦dϕ由坐标系旋转速度为=ω,则ϕ=ωt+ϕ(ϕ为初始角位置)1100dt(1)当ω=ω时,ϕ=ωt=ωt+ϕ,则1103i=−Isinϕ,sdm023i=−Icosϕ,sqm02223i=i+i=I;ssdsqm2(2)当ω>ω和ω<ω时,设ω=ω−ω,ωt−ϕ=−ωt−ϕ,则11s1s0⎡isd⎤3⎡Imsin(ωt−ϕ)⎤3⎡−Imsin(ωst+ϕ0)⎤⎢⎥=⎢⎥=⎢⎥。⎣isq⎦2⎣−Imcos(ωt−ϕ)⎦2⎣−Imcos(ωst+ϕ0)⎦6-3按转子磁链定向同步旋转坐标系中状态方程为\n坐标系的旋转角速度为Lmω=ω+i1stTψrr假定电流闭环控制性能足够好,电流闭环控制的等效传递函数为惯性环节dism11*=−i+ismsmdtTTiidist11*=−i+iststdtTTii**T为等效惯性时间常数。画出电流闭环控制后系统的动态结构图,输入为i和i,输出为ismstω和ψ,讨论系统稳定性。r解:电流闭环控制后系统的动态结构图如下:*ism1ismLmψrTs+1Ts+1ir*ist1istLmTenpωnpTis+1Lr_JsTL转子磁链环节为稳定的惯性环节;转速通道存在积分环节,系统不稳定,必须加转速外环使之稳定。6-4鼠笼异步电动机铭牌数据为:额定功率P=3kW,额定电压U=380V,额定电流NNI=6.9A,额定转速n=1400rmin,额定频率f=50Hz,定子绕组Y联接。由实NNN验测得定子电阻R=1.85Ω,转子电阻R=2.658Ω,定子电感L=0.294H,转子自感srsL=0.2898H,定、转子互感L=0.2838H,转子参数已折合到定子侧,系统的转动惯rm2量J=0.1284kg⋅m,电动机稳定运行在额定工作状态,试求转子磁链ψ和按转子磁链定r向的定子电流两个分量i和i。smst解:额定转速n=1400rmin,额定频率f=50Hz,则电动机极对数n=2,额定转NNp2πnN速ω==146.6(rads);ω=nω=293.2(rads);mpm60设三相正弦对称电流i=Isin(2πft)=9.758sin(100πt)、AmN2π2πi=Isin(2πft−)=9.758sin(100πt−)、BmN33\n2π2πi=Isin(2πft+)=9.758sin(100πt+),CmN33⎡⎤⎡11⎤⎢Imsin(2πfNt)⎥⎡i⎤2⎢1−−⎥⎢2π⎥⎡11.951sin(100πt)⎤sα22⎢⎥=⎢⎥⎢Imsin(2πfNt−)⎥=⎢⎥⎣isβ⎦3⎢03−3⎥⎢3⎥⎣−11.951cos(100πt)⎦⎢⎣22⎥⎦⎢Isin(2πft+2π)⎥mN⎢⎣3⎥⎦L0.2898r转子电磁时间常数T===0.109(s),rR2.658r电动机稳定运行在额定工作状态时ψ=Li−ωTψrαmsαrrβ,得ψ=Li+ωTψrβmsβrrαLi−ωTLimsαrmsβψ=rα221+ωTr0.2838×11.951×sin(100πt)−293.2×0.109×0.2838×(−11.951)×cos(100πt)=221+293.2×0.109=0.0033×sin(100πt)+0.1060×cos(100πt)Li+ωTLimsβrmsαψ=rβ221+ωTr0.2838×(−11.951)×cos(100πt)+293.2×0.109×0.2838×11.951×sin(100πt)=221+293.2×0.109=−0.0033×cos(100πt)+0.1060×sin(100πt)22222ψ=0.0033×sin(100πt)+0.0006996×sin(100πt)×cos(100πt)+0.1060×cos(100πt)rα22222ψ=0.0033×cos(100πt)−0.0006996×sin(100πt)×cos(100πt)+0.1060×sin(100πt)rβ2222ψ=ψ+ψ=0.0033+0.1060≈0.1061rrαrβψrβ−0.0033×cos(100πt)+0.1060×sin(100πt)sinϕ==ψ0.1061r≈−0.0311×cos(100πt)+0.9991×sin(100πt)ψ0.0033×sin(100πt)+0.1060×cos(100πt)rαcosϕ==ψ0.1061r≈0.0311×sin(100πt)+0.9991×cos(100πt)⎡ism⎤⎡cosϕsinϕ⎤⎡isα⎤⎡cosϕsinϕ⎤⎡sin(100πt)⎤⎢⎥=⎢⎥⎢⎥=11.951×⎢⎥⎢⎥⎣ist⎦⎣−sinϕcosϕ⎦⎣isβ⎦⎣−sinϕcosϕ⎦⎣−cos(100πt)⎦⎡0.0311⎤⎡0.3717⎤=11.951×⎢⎥=⎢⎥(A)⎣−0.9991⎦⎣−11.9402⎦6-5根据习题6-3得到电流闭环控制后的动态结构图,电流闭环控制等效惯性时间常数T=0.001s,设计矢量控制系统转速调节器ASR和磁链调节器AψR,其中,ASR按典型iII型系统设计,AψR按典型I型系统设计,调节器的限幅按2倍过电流计算,电动机参数同习题6-4。\n解:(1)AψR按典型I型系统设计**ψrism1ismLmψrΑΨRTs+1Ts+1_ir磁链调节器AψR采用PI调节器,其传递函数可写成K(τs+1)ψψW=AΨRτsψ磁链环开环传递函数为Kψ(τψs+1)LmW=opψτs(Ts+1)(Ts+1)ψirL0.2898r其中转子电磁时间常数T===0.109(s),电流闭环控制等效惯性时间常数rR2.658rT=0.001s,选择τ=T=0.109s,便校正成典型I型系统,因此iψrKψLmKΨKψLmW==,其中:K=;opψΨτs(Ts+1)s(Ts+1)τψiiψ在一般情况下,希望超调量σ≤5%,可选择ξ=0.707,KT=0.5,则iΨi1−1K=ω==500(s),Ψcψ2TiKΨτψKΨTr500×0.109K====192.04,ψLL0.2838mm调节器的限幅按2倍过电流计算,磁链调节器AψR输出限幅值*i=2i=2×0.3717=0.7434(A)。smmaxsmN(2)ASR按典型II型系统设计ψTrL_**i1istLTenωωstmpASRnp_Tis+1LrJs转速调节器ASR采用PI调节器,其传递函数可写成K(τs+1)nnW=ASRτsn转速环开环传递函数为2Kn(τns+1)1npLmnpKnnpLmψr(τns+1)W=ψ=opnr2τsTs+1LJsτLJs(Ts+1)nirnri2KnLψnpmr令转速环开环增益K=,则NτLJnrK(τs+1)W=Nnopn2s(Ts+1)i按跟随和抗扰性能都较好的原则,取中频宽h=5,则τ=hT=5×0.001=0.005(s)ni\nh+15+1−2−2K==s=120000sN22222hT2×5×0.001iKτLJ120000×0.005×0.2898×0.1284NnrK==≈185.365n22nLψ2×0.2838×0.1061pmr−1−1转速环截止频率ω=Kτ=120000×0.005s=600scnNn调节器的限幅按2倍过电流计算,转速调节器ASR输出限幅值*i=2i=2×11.9402=23.8804(A)stmaxstN查看更多