[农学]理论力学第2章

[农学]理论力学第2章

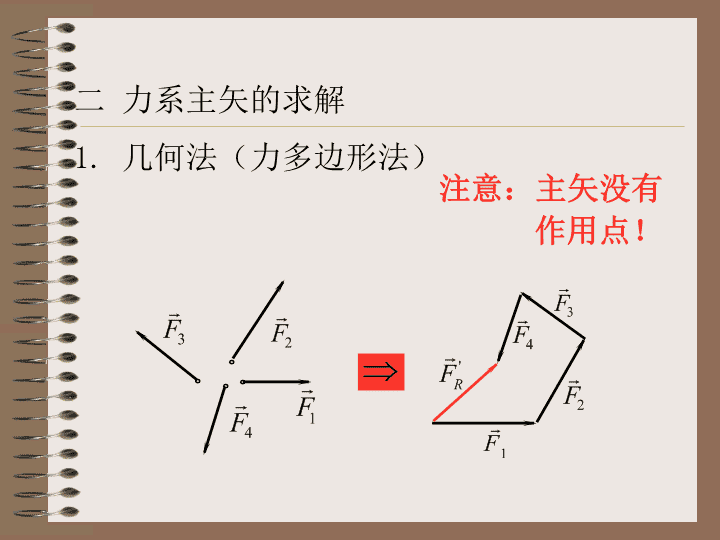
第二章力系的简化\n§2-1力系的主矢与主矩一力系的主矢指力系中力矢的几何和\n二力系主矢的求解1.几何法（力多边形法）注意：主矢没有作用点！\n2解析法的三个投影为：力系的主矢\n主矢的方向余弦:力系的主矢\n三力系的合力如果满足一定条件的一个已知力系可以与单个力等效，此等效力称为该力系的合力。性质三要素大小方向作用点主矢合力几何量有有有有有无可在任意点画出任何力系均有主矢不是所有的力系都有合力物理量力系的主矢\n四力系的主矩1.定义：力系中各力对任一点的矩的几何和称为力系对该点的主矩力系的主矩\n主矩:力系的主矩\n即:力系的主矩\n2、同一力系对不同点的主矩之间的关系则力系对A点之矩：在一般情况下，力系的主矩随矩心位置的不同而变化，只有在特殊情况下(或）,主矩才保持不变。另选矩心A，各力作用点对于矩心A的矢径为:力系的主矩\n例1：长方体OABCDEGH上作用着三个力，大小均为F，b已知，求这个力系的主矢和主矩。求力系的主矢：即求各力在坐标轴上的投影方法一：直接投影法：若已知力与某轴的夹角，可直接求出力在此轴上的投影。\n方法二：两次投影法：\n\n求力系的主矩：即求各力对在坐标轴上的矩方法一：利用分力计算力矩：\n\n方法二：利用定义：\n\n§2.2力系的简化2.2.1力的平移定理ABABAB\n作用在刚体上的力可以平移到刚体上任一点,但必须同时附加上一个力偶，该附加力偶的矩等于原来力对新作用点的矩。ABAB\nOAd一个力不仅可以分解为几个力，还可以分解为力和力偶。O\n2.2.2力系等效定理矩心O是任意选择的充要条件：两力系的主矢相等，对同一点的主矩相等.\n2.2.4力系的简化＝（一）简化过程2.2.4.1空间力系的简化\n＝空间任意力系向任意一点简化，一般得一个主矢和一个主矩（二）简化结果\n（三）空间任意力系简化结果的讨论（1）主矢和主矩都为零力系的合成结果是一力偶，力系的主矩与矩心位置无关平衡力系（2）主矢为零，主矩不为零（3）主矩为零，主矢不为零力系的合成结果是一力，且（4）主矢和主矩都不为零\na.=简化为作用于O1的合力FR’\nb.力螺旋主矢与主矩方向一致时，称为右手螺旋，否则称为左手螺旋。\nc.FR与Mo成任意角度\n2.2.4.2平面力系的简化\n主矢的计算：主矩的计算：\n2.2.4.3固定端约束力的分析固定端的约束力可以简化为作用在约束处的一个约束力和一个约束力偶。\n例2（1）求这三个力向A点和D点简化的结果，（2）力系的合成结果。\n解（1）求力系的主矢：将各力分别向x、y轴投影：\n对A、D点的主矩分别为：\n力系的合成结果为一合力\n空间平行力系，当它有合力时，合力的作用点C就是此空间平行力系的中心。§2.3平行力系的中心物体的重心2.3.1空间平行力系的中心FR\nFR由合力矩定理：\n例3求梁上按三角形分布的线载荷的合力。已知梁长l，B处的载荷集度为q。求合力的作用点。\n解：\n均布载荷非均布载荷结论：按任一平面曲线分布的线载荷，其合力的大小等于载荷图的面积，作用线通过载荷图形的形心，合力的指向与分布力的指向相同\n重力合力作用线所通过的确定点，叫做该物体的重心。2.3.2重心由合力矩定理：\n设i表示第i个小部分每单位体积的重量，⊿Vi第i个小体积，则代入上式并取极限，可得：式中，上式为重心C坐标的精确公式。对于均质物体，=恒量，上式成为：同理对于薄平面和细长杆均可写出相应的公式。\n若以△Pi=△mig,P=Mg代入上式可得质心公式\n同理：可写出均质体，均质板，均质杆的形心（几何中心）坐标分别为：\n解：由于对称关系，该圆弧重心必在Ox轴，即yC=0。取微段下面用积分法求物体的重心实例：[例]求半径为R，顶角为2的均质圆弧的重心。O\n重心的求法：①组合法解：求：该组合体的重心？已知：\n简单图形的面积及重心坐标公式可由表中查出。②实验法：<1>悬挂法<2>称重法