《大学化学复习》PPT课件

《大学化学复习》PPT课件

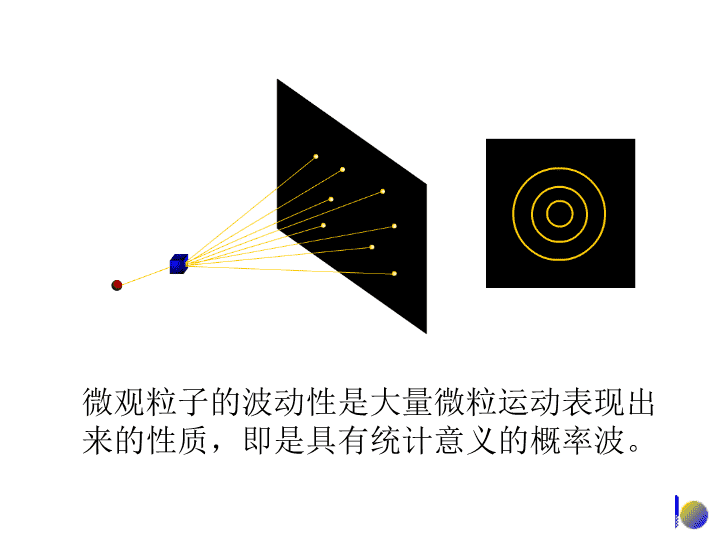
1927年，电子衍射的实验证实了德布罗意的预言，电子不仅是一种具有一定质量，高速运动的带电粒子，而且还能呈现波动性。电子波动性的证明\n微观粒子的波动性是大量微粒运动表现出来的性质，即是具有统计意义的概率波。\n电子波动性的证明得出的结论：波动性是与微粒行为的统计性规律在一起的。在底片上衍射强度大的地方（明处），也就是波强度大的地方，一定是电子在该处单位微体积内出现的机会多（概率密度大），衍射强度小的地方（暗处），也就是波强度小的地方，一定是电子在该处单位微体积内出现的机会少（概率密度小）。由此可以认为：具有波动性的微观粒子（包括电子在内）虽然没有确定的运动轨迹，但在空间某处波的强度与该处粒子出现的概率密度成正比。\n（2）波函数的角度分布图①原子轨道的角度分布图②电子云的角度分布图③原子轨道与电子云角度分布图比较\n①原子轨道的角度分布图\n波函数ψ=薛定谔方程的合理解=原子轨道①原子轨道的角度分布图三个量子数n,l,m确定的波函数称为一个原子轨道波函数ψ是量子力学中描述核外电子在空间运动状态的数学函数式，量子力学借用经典力学中描述物体运动的“轨道”的这一名词，把波函数ψ叫做原子轨道。n=1,l=0,m=0,ψ1,0,01s原子轨道,ψ1sn=2,l=0,m=0,ψ2,0,02s原子轨道,ψ2sl=1,m=0,ψ2,1,02pz原子轨道,ψ2pz\n②电子云的角度分布图与原子轨道的角度部分相对应，也有电子云即概率密度|ψ|2的角度部分|Yl,m(θ,φ)|2的分布图。例如pz电子云的角度部分是|Ypz|2=cos2θ，若将|Ypz|2对θ作图，便可得到pz电子云的角度分布图。它表示了电子在空间不同角度出现的概率密度的大小，从角度的侧面反映了电子云概率密度分布的方向性。\n②电子云的角度分布图\n②电子云的角度分布图电子云也可以是用统计的方法描述电子在核外空间某一区域内出现概率大小的一个形象化的图示，s电子经常出现的区域是核外的一个球形空间。图中密集的小点只是说明氢原子核外的一个电子在核外空间的一种运动状态，并不代表有这么多个电子在核外运动。s电子云l=0\n②电子云的角度分布图处于不同状态的电子，它们的波函数ψ各不相同，其|ψ|2当然也各不相同，表示|ψ|2的图像——电子云图也不一样。\n③原子轨道与电子云角度分布图比较★形状相似，不同的是电子云的角度分布图形比原子轨道的角度分布图形要“瘦”些；这是由于Y=cos值小于1，而|Y|2值就更小的缘故。★正负号不同，原子轨道角度分布图上有＋、－号之分，而电子云角度分布图上都是正值；原子轨道角度分布图上的＋、－号只是代表波函数ψ中角度部分Y的正、负，并不表示波函数ψ的正、负。\n3.四个量子数由n、l、m三个量子数所确定下来的一套参数就可以表示一种波函数。在求解薛定谔方程的过程中除了直接引入的这三个量子数之外，后来根据实验和理论的要求，又引入了一个描述电子自旋特征的量子数ms。这些量子数对描述核外电子的运动状态、确定原子中电子的能量、原子轨道或电子云的形状和空间伸展方向、以及多电子原子核外电子的排布非常重要。\n3.四个量子数－主量子数主量子数nn=1，2，3，4，5，6，7……（正整数）①主量子数n是决定电子层数的。用它来描述原子中电子出现概率最大的区域离核的远近。n的取值范围：K，L，M，N，O，P，Q……（光谱符号）\n3.四个量子数－主量子数主量子数n核外电子能量既与n有关，又与l有关，取决于n和l的取值。不能只决定于n值的大小。②主量子数n是决定电子能量高低的主要因素。对多电子原子：\n3.四个量子数－角量子数角量子数l（亦称副量子数）①角量子数l表示原子轨道或电子云的形状。l的取值范围：对于给定的n值，l只能取小于n的整数值。l=0，1，2，3，4，5……(n-1)s，p，d，f，g，h……（光谱符号）\n3.四个量子数－角量子数角量子数l（亦称副量子数）②用主量子数n表示电子层时，角量子数l就表示同一电子层中具有不同状态的分层，对于给定的主量子数n来说，就有n个不同的角量子数l。电子层数n值电子分层l值电子分层数101s2012s2p30123s3p3d401234s4p4d4f\n3.四个量子数－磁量子数磁量子数m①磁量子数m决定原子轨道或电子云在空间的伸展方向。m的取值与角量子数l有关，对于给定的l值，有2l+1个m的取值，可以取从l到－l的所有整数，其中包括零：m=0，±1，±2，±3······±l。\n3.四个量子数－磁量子数磁量子数m①磁量子数m决定原子轨道或电子云在空间的伸展方向。l=0，s电子m=0一种状态在空间无方向性l=1，p电子m=0，±1三种状态在空间有三种取向l=2，d电子m=0，±1，±2五种状态在空间有五种取向l=3，f电子m=0，±1，±2，±3七种状态在空间有七种取向角量子数l与磁量子数m的关系\n3.四个量子数－自旋量子数ms表示电子自旋运动的状态，取值只有两个：自旋量子数ms直接从薛定谔方程得不到自旋量子数ms，它是据后来的理论和实验的要求引入的。精密观察强磁场存在下的原子光谱，每一条谱线实际是由靠得很近的两条谱线组成的。为了解释这一现象，1925年乌伦贝克（Uhlenbeck）和哥德希密特（Goudsmit）提出了电子自旋的假设。12ms=+，–12\n3.四个量子数四个量子数确定后，电子在核外空间的运动状态就确定了原子中每个电子的运动状态需要用n，l，m，ms四个量子数来描述；主量子数n决定电子层数和主要决定电子的能量；角量子数l决定原子轨道的形状，同时也影响电子的能量；磁量子数m决定原子轨道在空间的伸展方向；自旋量子数ms决定电子自旋的方向；◆◆◆◆◆\n4.核外电子的运动状态小结（2）在微观世界中，核外电子运动的能量是不连续的，分为不同的能级（n），电子运动的每一个状态均需要用四个量子数（n、l、m、ms）来确定。（1）电子是微观粒子，具有波粒二象性，不能同时确定其位置和动量，它的空间运动状态需要用波函数ψ来描述。（3）波函数、原子轨道、电子云的区别和联系：★四个量子数n、l、m、ms确定电子的一种空间运动状态。★三个量子数n、l、m确定一个波函数ψn,l,m，波函数ψ就是原子轨道；电子云就是描述电子出现的概率||2.\n4.核外电子的运动状态小结★原子轨道和电子云的图象形状相似，不同是原子轨道的图象中有正、负号，电子云的图象中则没有。原子轨道的正、负号在原子轨道组合成分子轨道时会起到关键的作用。（3）波函数、原子轨道、电子云的区别和联系：（4）四个量子数之间互相联系又互相制约，同一个原子中没有彼此状态完全相同的电子，或者说，在同一个原子中不可能有四个量子数完全相同的两个电子存在。\n保里（W.Pauli）不相容原理能量最低原理洪德（F.Hund）规则2.核外电子排布的原理\n全充满、半充满规则等价原子轨道（n，l相同的亚层）处于全充满(p6、d10、f14)，半充满（p3、d5、f7）或全空（p0、d0、f0）的状态时，体系能量较低，状态较稳定。例：24Cr3d54s1（）3d44s2（）29Cu3d104s1（）3d94s2（）\nZ=11，Na：1s22s22p63s1或[Ne]3s1，Z=20，Ca：1s22s22p63s23p64s2或[Ar]4s2，Z=50，Sn：[Kr]4d105s25p2，Z=56，Ba：[Xe]6s2。[Ne]、[Ar]——原子实\n2.元素基本性质的周期性（2）电离能的周期性一般规律：●同一周期（短周期）自左向右，电离能递增；（核电荷数增多，原子半径减小，原子核对外层电子的引力增大）●各周期中稀有气体的电离能最大，因为它们的原子具有稳定的8电子结构；●同一主族元素自上而下，电离能总趋势是减小；（电子层数增加，原子半径增大，原子核对外层电子的引力减小起主导作用，核电荷数增大，核对电子的吸引力增大这一因素不起主导作用）\n2.元素基本性质的周期性（2）电离能的周期性一般规律：●同一周期过渡元素电离能增加程度较小；因其原子半径减小的程度小，Mn和Zn的电离能比其前面元素Cr和Cu增加较多，因为Mn和Zn的d轨道半充满和全充满；●同一元素各级电离能的大小规律：I1＜I2＜I3＜…；●电离能的数据能说明元素的金属活泼性和元素的常见氧化态；\n2.元素基本性质的周期性（2）电离能的周期性反常现象：◆同一周期主族元素N＞O，P＞S；O和S外层失去1个电子后，p轨道半充满稳定结构，故电离能小于其前面的元素；◆同一周期过渡元素Mn和Zn分别具有半充满和全充满的d轨道稳定结构，不易失去电子，故电离能比其前面的元素增加较多；VCrMn……NiCuZn651653717737746906\n电子亲和能是指一个气态原子得到一个电子形成负离子时放出或吸收的能量，常以符号Ea表示。像电离能一样，电子亲和能也有第一、第二、…之分。元素第一电子亲和能的正值表示放出能量,负值表示吸收能量。电子亲和能是气态原子获得一个电子过程中能量变化的一种量度；与电离能相反，电子亲和能表达原子得电子难易的程度；元素的电子亲和能越大，原子获取电子的能力越强，即非金属性越强。2.元素基本性质的周期性（3）电子亲和能的周期性\n第二章分子结构MolecularStructure\n（3）共价键的特征①具有饱和性每种元素的原子提供能用于形成共价键的轨道数和成单电子的数目是一定的；NNHClHOHHH\n（4）共价键的键型键的类型键键原子轨道重叠方式沿键轴方向头碰头沿键轴方向肩并肩原子轨道重叠部位两原子核之间，在键轴处键轴上方和下方，键轴处为零原子轨道重叠程度大小键的强度较大较小化学活泼性不活泼活泼键和键的特征比较\n（1）杂化轨道类型s-p型杂化s-p型杂化小结杂化轨道类型参加杂化的轨道数目杂化轨道数目杂化轨道中键角空间构型sps含量p含量sp1121/21/2180°直线sp21231/32/3120°平面三角形sp31341/43/4109.5°四面体在s-p型杂化中，键角随着杂化轨道中s含量的增加而变大；等性杂化杂化轨道性质等同\n（2）分子间作用力分子偶极矩越大，定向力(取向力)越大极性分子偶极矩越大，诱导力越大范德华力：取向力、诱导力、色散力\n分子的极性分子间力的种类产生的原因非极性分子之间色散力瞬时偶极非极性分子与极性分子之间色散力诱导力瞬时偶极诱导偶极极性分子之间色散力诱导力取向力瞬时偶极诱导偶极永久偶极分子间力及产生的原因（2）分子间作用力\n分子间力是决定物质熔、沸点、溶解度等物理化学性质的一个重要因素。范德华力特点：（1）存在于分子或离子间的一种作用力；（2）吸引力，其作用能相当小，范围只有几个pm；（3）一般没有方向性和饱和性；（4）色散力存在于任何分子之间，是主要的分子间力；（2）分子间作用力\n(3)氢键HydrogenBond（A）氢键的形成（B）氢键的特点（C）氢键的类型（D）氢键对化合物性质的影响\n晶体的定义晶体是由原子或分子在空间按一定规律周期性地重复排列构成的固体物质。注意（1）一种物质是否是晶体是由其内部结构决定的，而非由外观判断；（2）周期性是晶体结构最基本的特征。\n3-1晶体的宏观性质（2）晶体具有规则的几何构形，这是晶体最明显的特征，同一种晶体由于生成条件的不同，外形上可能差别，但晶体的晶面角（interfacialanglt）却不会改变。钻石—晶体玻璃—非晶体\n3-1晶体的宏观性质（3）晶体都有固定的熔点，非晶体在加热时却是先软化，后粘度逐渐小，最后变成液体。\n3-1晶体的宏观性质（4）晶体表现各向异性，例如热、光、电、硬度等常因晶体取向不同而异；而非晶体则为各向同性。例：云母沿层状结构方向易被剥离例：石墨层内导电率比层间高一万倍\n3-1晶体的宏观性质（5）宏观上判断晶体与非晶体，应综合以上三方面的特点来考察，单从一方面进行判断是不充分的。为什么晶体与非晶体上存在如此大的差异？内部结构不同（结构决定性质，性质反映结构）如何探测内部结构？衍射实验（X衍射和电子衍射）\n关于晶体与非晶体从热力学的角度看晶体一般都具有最低能量，因而较为稳定；非晶体一般能量较高都处于介稳或亚稳态。晶体和非晶体之间无绝对界线同一物质在不同条件下既可形成晶体，又可形成非晶体，彼此之间在一定条件下可以实现转化。\n一、反应速率理论简介小结（1）无论是吸热反应还是放热反应，都要经过一个中间过渡状态，反应物分子必须先爬过一个能峰，即克服反应活化能，反应才能进行。（2）不同的化学反应具有不同的活化能，一定温度下，反应的活化能越大，能峰越高，活化分子数越少，反应速率越慢；反之，活化能越小的反应速率越快。（3）活化络合物极不稳定，可以分解为产物，也可以分解为反应物，反应速率取决于活化络合物的浓度及其分解频率。正逆反应活化能之差为反应的摩尔焓变。\n四、温度对反应速率的影响（1）改变反应温度，改变了反应中活化分子的百分数，但并没有改变反应的活化能。（2）无论吸热反应还是放热反应，温度升高，反应速率都要加快。这两者在反应过程中反应物都必须爬过一个能垒，反应才能进行，升高温度，有利于反应物能量提高，故两者的反应速率都要加快。不过吸热反应速率加快的程度大于放热反应。注意：\n五、催化剂对反应速率的影响催化剂是一种能改变化学反应速率，其本身在反应前后质量和化学组成均不改变的物质。催化剂之所以能改变化学反应速率，是因为它参与了化学变化过程，改变了反应原来的途径，降低了活化能。\n五、催化剂对反应速率的影响催化剂改变了反应途径，反应沿一条活化能低的捷径进行，因而速率加快。\n五、催化剂对反应速率的影响合成氨反应，没有催化剂时反应的活化能为326.4kJ·mol-1，加Fe作催化剂时，活化能降低至175.5kJ·mol-1。催化剂不影响产物和反应物的相对能量，没有改变反应的始态和终态，所以催化剂只能改变反应途径而不能改变反应发生的方向。从图中还可以看到，加入催化剂后，正、逆反应的活化能降低的数值相等，这意味着催化剂同等程度地加快正、逆反应的速率。\n五、催化剂对反应速率的影响催化剂同等程度地加快正、逆反应的速率，所以催化剂只能加速化学平衡的到达，不能改变平衡点的位置。催化剂虽然改变了反应原来的途径，降低了活化能，但不能改变反应的G，对一个G＞0的反应，想用催化剂改变其反应方向是徒劳的。\n（3）标准生成焓与反应热的关系反应物产物各种单质321∑fHm（产物）Ө∑fHm（反应物）ӨrHmӨ途径1=途径(2+3)H3=H1－H2物质的标准生成焓数据计算化学反应的热效应\n（3）标准生成焓与反应热的关系(4-3)rHm=∑fHm(产物)-∑fHm(反应物)ӨӨӨ要求会查表用标准生成热fHm数据求算某一反应的焓变rHm；ӨӨ\n（3）标准生成焓与反应热的关系2Na2O2(s)+2H2O(l)→4NaOH(s)+O2(g)[例题2]求下列反应的标准摩尔反应热rHm：Ө解：由公式(4-3)式计算rHm=∑fHm(产物)–∑fHm(反应物)=[4fHm(NaOH,s)+fHm(O2,g)]–[2fHm(H2O,l)+2fHm(Na2O2,s)]ӨӨӨӨӨӨӨ\n（3）标准生成焓与反应热的关系通过查表找出各产物和反应物的标准生成热数据，进行如下计算。查表得：fHm(NaOH,s)=-426.7kJ·mol-1fHm(Na2O2,s)=-513.2kJ·mol-1fHm(H2O,l)=-285.83kJ·mol-1O2是稳定单质,fHm(O2,g)=0求算反应热:rHm=[4×(-426.7)+0]–[2×(-513.2)+2×(-285.83)]=-108.9(kJ·mol-1)是个放热反应ӨӨӨӨӨ\n1.可逆反应与化学平衡当正、逆反应速率相等、反应物和生成物的浓度不再随时间而变化时，称体系达到了热力学平衡状态，简称化学平衡。\n【小结】化学平衡的判断依据正逆反应速率相等各组分的浓度保持不变\n2.3.书写平衡常数表达式的规则（4）当n个反应相加或相减得到某一反应时，其反应的平衡常数等于各相加反应的平衡常数的乘积或商，这是多重平衡规则。K3=K1·K2ӨӨӨ如果反应(3)=反应(1)+反应(2)如果反应(4)=反应(1)–反应(2)K4=K1/K2ӨӨӨ\n3.平衡常数与转化率转化率反应物初始浓度-反应物平衡浓度反应物初始浓度=×100%用平衡常数估计反应进行的可能性，判断反应的程度，只能得到一个大致的结果。一定量的反应物到底能生成多少产物，要通过定量计算反应物转化为产物的转化率。当一个反应达到平衡时，反应物的转化率为：\n浓度、温度、压强对化学平衡的影响条件适应范围对化学平衡的影响导致的结果浓度除固体外增大反应物浓度（减小生成物浓度），向正反应移动；减小反应物浓度（增大生成物浓度）向逆反应移动反应物浓度减小（生成物浓度增加）反应物浓度增加（生成物浓度减小）增大浓度，结果是减小浓度压强适应气体增大压强，向体积缩小的方向移动；减小压强，向体积增大的方向移动体积缩小，减小压强体积增大，增大压强增大压强，结果是减小压强温度全部升高温度，向吸热反应方向移动；降低温度，向放热反应方向衔动反应吸絷，温度降低反应放热，温度升高升高温度，结果是降低温度\n思考下列反应达到平衡时：2SO2(g)+O2(g)===2SO3(g)如果在其它条件不变时，分别改变下列条件：（1）增加压强（2）增大O2的浓度（3）减少SO3的浓度（4）升高温度（5）使用催化剂，将对化学平衡有什么影响？简要说明理由\n[例题4]已知下列平衡体系（反应容器为1L）在830℃时的Kc=1.0，若初始浓度[CO]=2mol·L–1，[H2O]=3mol·L–1，求算达到平衡时，各物质的浓度为多少？CO的转化率为多少？CO(g)+H2O(g)H2(g)+CO2(g)解：设在平衡时[CO2]=xmol·L–1，初始浓度/mol·L–12300平衡浓度/mol·L–12-x3-xxx各物质的平衡浓度：[CO2]=[H2]=1.2mol·L–1[CO]=2-1.2=0.8mol·L–1[H2O]=3-1.2=1.8mol·L–1CO转化为CO2的转化率为5计算题\nCO(g)+H2O(g)H2(g)+CO2(g)解：设在平衡时又有ymol·L–1的CO转化为CO2，初始浓度/mol·L–10.81.81.21.2平衡浓度/mol·L–10.8-y1.8+1.2-y1.2+y1.2+y解一元二次方程式，得到y=0.15[例题5]如果温度和体积不变，在上述平衡体系中加入1.2mol·L–1的H2O(g)，当再达到平衡时，各物质的浓度为多少？CO转化为CO2的转化率为多少？计算题\nCO(g)+H2O(g)H2(g)+CO2(g)解：设在平衡时又有ymol·L–1的CO转化为CO2，初始浓度/mol·L–10.81.81.21.2平衡浓度/mol·L–10.8-y1.8+1.2-y1.2+y1.2+y各物质的平衡浓度：[CO2]=[H2]=1.2+0.15=1.4mol·L–1[CO]=0.8-0.15=0.65mol·L–1[H2O]=1.8+1.2-0.15=2.9mol·L–1CO转化为CO2的转化率为[例题5]如果温度和体积不变，在上述平衡体系中加入1.2mol·L–1的H2O(g)，当再达到平衡时，各物质的浓度为多少？CO转化为CO2的转化率为多少？计算题\n3、弱酸弱碱的解离平衡弱酸弱碱解离平衡公式小结\n3.缓冲溶液的pH值(8-7)(8-8)(8-19)(8-20)\n沉淀溶解平衡计算例题：[例题1]通过溶解度s求算Ksp在25℃时，Ag2CrO4的溶解度s为2.6×103g·(100g水)1，求该温度下Ag2CrO4的Ksp\n（1）内界，外界[Co(NH3)6][Cr(CN)6]\n（3）配体(配位个体)与配位原子NCH2CH2NNaOOCH2CHOOCH2CCH2COOHCH2COONaEDTA\n（4）配位数\n3.配位化合物的类型(螯合物)二氨基乙酸合铜(Ⅱ)EDTA与Ca2+的配合物螯合物（4）五个五元环\n（2）计算配离子溶液中有关离子的浓度\n（2）计算配离子溶液中有关离子的浓度\n1.配合物的稳定常数◆对相同类型的配离子，可直接用其Kf的大小来比较它们的稳定性；1.3×1021\n1.配合物的稳定常数\n1.配合物的稳定常数1.3×10211.3×10217.7×1021mol·L1\n（2）标准氢电极和标准电极电势◆标准电极电势表\n3.电池电动势与吉布斯自由能的关系例题2E池值。Ө将值代入（10−2）公式中：Ө△rGm−229.7kJ·mol–1=−2×96485C·mol–1×E池ӨrGm=−nF·E池ӨӨE池=1.35VӨ\n（1）能斯特方程ӨE池=E池−·lg例题5：计算下列条件下的Cu-Zn原电池的电动势。Zn(s)+Cu2+(c1)→Cu(s)+Zn2+(c2)E池=1.10V−·lg=1.10V−0.0295V×1.30=1.06V解：c1=0.020mol·L1，c2=0.40mol·L1，E池=1.10VӨ\n