大学物理d-习题
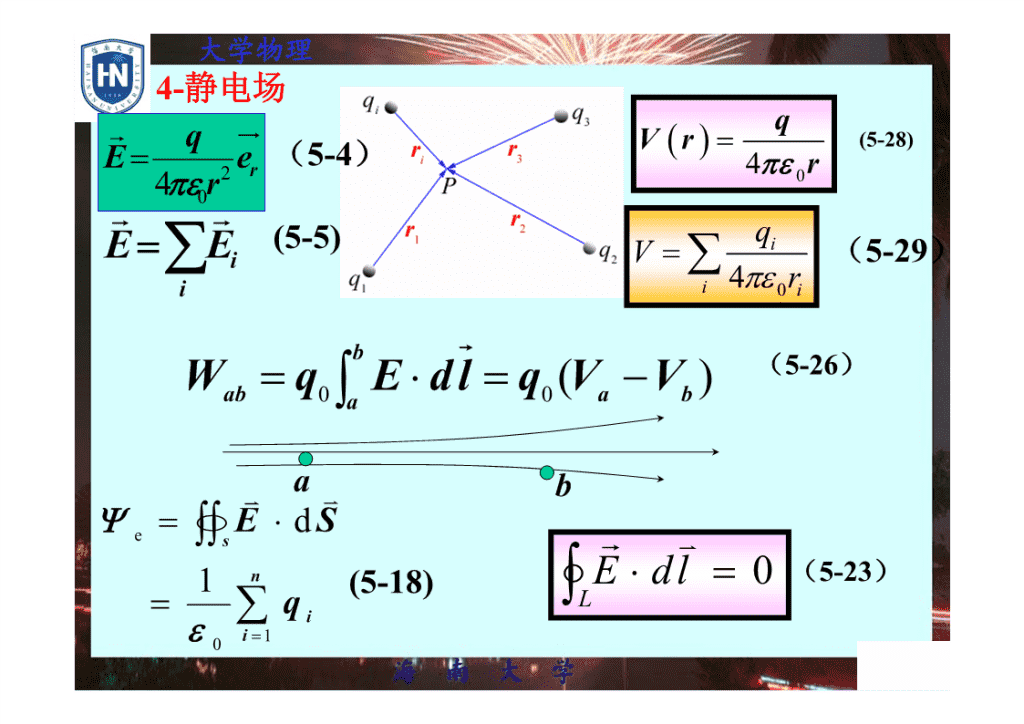
大学物理\n大学物理4-静电场rqqVr()=(5-28)E=2er(5-4)4πε0r4πεr0rrE=E(5-5)qi∑iV=∑(5-29)ii4πε0rib(5-26)W=qE⋅dl=q(V−V)ab0∫a0abvavbΨ=E⋅dSe∫∫srv1n(5-18)∫E⋅dl=0(5-23)=∑qLiεi=10\n4.4.1大学物理−6在x轴上,有一点电荷qC1=×2010,位于原点,另一−6点电荷qC=×5010,位于x=-10cm处。试求x轴2上任一点的电场强度。qq12321解:1)x>0−0.100qq12412.05.0−E=+=9.010[×+]Vm⋅22224πεxx4(0πε++.10)x(0x.10)002)0.10
0.25s)试求(1)P点的振动表式;(2)此波的波动表式;y(m)0.2t=01x(m)oP−0.2t2=0.25s0.45\n大学物理解:由波形图得A=0.2mλ=0.6mΔx0.15u===0.6(m/s)Δt0.250.6λ==1(s)T=u0.6x设波动表达式y=Acos[ω(t−)+ϕ0]u由t=0时的波形图及结合旋转矢量图,得ϕ=π/20(2)波动表达式x2πxπ10πy=Acos[ω(t−)+ϕ]=0.2cos[(t−)+]=0.2cos[2πt−πx+]m0u10.6232(1)P点的振动表达式10ππy=0.2cos[2πt−π×0.3+]=0.2cos[2πt+]mP322\n大学物理6.4.4波动表式为y=0.05cos(10πt-4πx)(SI制)横波沿绳子传播。(1)求此波的振幅、波速、频率和波长。(2)求绳子上各质点振动的最大速度和最大加速度。(3)求x=0.2m处的质点在t=1s时的相位,它是原点处质点在哪一x时刻的相位?y=Acos[ω(t−)+ϕ]0xu解(1)y=0.05cos(10πt−4πx)=0.05cos10π(t−)5/2A=0.05mv=2.5m/sω=10πrad/sv=ω/2π=5.0Hzλ=uT=u/ν=2.5/5.0=0.5m(2)υ=Aω=0.05×10π=0.5π≈1.57(m/s)m222≈m/s2a=Aω=0.05×100π=5π49.3()m(3)ϕϕ=10π×1−4π×0.2=9.2π(或0.8π);ϕ=10π×t−4π×0,t==0.92(s)10π\n大学物理6.4.5设S和S为两相干波源,初始相位相差π,相12距4λ。若两波在S与S连线方向上连线方向上传播时12分别引起各点振动的振幅均为A,且不随距离变化,求S与S连线间由于干涉而振幅为2A的点的位置。12解:r1=S1P=xSpSr=SP=−x12224λrr−(4λ−xx)−4xπ21Δ=−−ϕϕϕπ22=−ππ=−7π2010λλλ当满足Δϕ=2kπ时,P点因干涉而振动加强,振幅为2A,17xk=+()λk=−−−3,2,1,0,1,2,3,42413579111315x,,,,,,,=λλλλλλλλ时,P点由于干涉44444444而振幅为2A。\n大学物理光学-干涉奇数次半波损失时为λ/2'光程差δ=Δ−Δ+δ21偶数次半波损失时为0光程Δ=∑niri±kλ(k=0,1,2⋅⋅⋅)干涉加强(明)δ=λ±(2k+1)(k=0,1,2⋅⋅⋅)干涉相消(暗)2dx±kλk=0,1,2,3L明纹δ=r2−r1==λD±()2k+1k=0,1,2,3L暗纹2D±kλx=dDλ±+(k)21d2\n大学物理λδ=2nd+=δ(d)2λ亮纹δ=2nd+=kλ,k=1,2,3L2λ()λ暗纹δ=2nd+=2k+1,k=0,1,2,L22λλd−d==ni+1i2n2λ2nθ≈DLθ≈b\n大学物理7.4.1用波长为500nm(1nm=10-9m)的单色光垂直照射到由两块光学平玻璃构成的空气劈形膜上.在观察反射光的干涉现象中,距劈形膜棱边l=1.56cm的A处是从棱边算起的第四条暗条纹中心。(1)求此空气劈形膜的劈尖角;(2)改用600nm的单色光垂直照射到此劈尖上仍观察反射光的干涉条纹,A处是明条纹还是暗条纹?(3)在第(2)问的情形从棱边到A处的范围内共有几条明纹?几条暗纹?解:(1)棱边处是第一条暗纹中心,在膜3厚度为λ/2处第二暗纹,依此e=λ42e−543λ4.810θ===×ll2rad(2)e=3×500/2nm=750nm4()2/e+λλ′′2/3=A处是明纹4(3)棱边处仍是暗纹,A处是第三条明纹,所以共有三条明纹,三条暗纹\n大学物理7.4.21.用很薄的云母片(n=1.58)覆盖在双缝实验中的一条缝上,这时屏幕上的零级明条纹移到原来的第七级明条纹的位置上。如果入射光波长为550nm,试问此云母片的厚度为多少?解法1:设云母的厚度为d。有云母时,光程差rPxdd1δ=−(n−1)dDS1r20x=0处的光程差δ=(n−1)dS2x=0处为第k=7级明纹时δ=(n−1)d=kλ−9λ550×10−6d=k=7×=6.64×10(m)n−11.58−1完\n大学物理解法2:设云母的厚度为d。有云母时,光程差δ′=[]()r−r+(n−1)drP12d1S1r2δ=[]()r−r012S2δ=[()r−r]=012δ′=[]()r−r+(n−1)d=kλ12(n−1)d=kλ−9λ550×10−6d=k=7×=6.64×10(m)n−11.58−1\n大学物理光学-衍射asinθN=λ2asinθ=±kλ,k=1,2,3…——暗纹λasinθ=±(2k′+1),k′=1,2,3…——明纹(中心)22λΔθ≈0afλΔx=ka\n大学物理分析明纹宽度中央明纹:两个一级暗纹间的距离,θ为1级暗纹对应的衍射角1asinθ=λ1θ≈sinθ11λθ=1Δθ=2θ中央明纹a01k=12λΔθ≈0ak=2上式为中央明纹角宽度\n大学物理中央明纹线宽度x2fλxΔx=2x=2ftgθ=2fθ=k0100ak=22fλk=1Δx=0中央aΔθ=2θO01明纹(a,λ)f其他明纹宽度asinθ=±kλk(2k1)f+λxx=kktgθ=k2aftgθ≈sinθfλkkΔx=ka\n大学物理光栅衍射(a+b)sinθ=±kλ(k=0,1,2,L)\n大学物理7.4.3有一单缝,宽a=0.10mm,在缝后放一焦距为50cm的会聚透镜,用平行绿光(=546.0nm)垂直照射单缝,试求位于透镜焦面处屏幕上中央明纹及第二级明纹的宽度。解:中央明纹宽度:−9λ546.0×10−3Δx=2DtgΔθ=2D=2×0.5=5.46×10(m)00−3a0.10×10第二级明纹宽度:λ−3Δx=DtgΔθ=D=2.73×10(m)a\n大学物理7.4.33.有一单缝,宽a=0.10mm,在缝后放一焦距为50cm的会聚透镜,用平行绿光(λ=546.0nm)垂直照射单缝,试求位于透镜焦面处屏幕上中央明纹及第二级明纹的宽度。解:中央明纹宽度λΔx=2DtgΔθ=2D00a−9546.0×10−3=2×0.5=5.46×10(m)−30.10×10\n7.4.3大学物理第二级明纹宽度λΔx=DtgΔθ=Da−9546.0×10−3=0.5×=2.73×10(m)−30.10×10完\n大学物理7.4.4在复色光照射下的单缝衍射图样中,其中某一未知波长光的第三级明纹极大位置恰与波长为=600nm光的第二级明纹极大位置重合,求这种光波的波长。解:λ′λ′asinθ=(2k′+1)=(2×3+1)22λλasinθ=(2k+1)=(2×2+1)2255λ′=λ=×600=428.6nm77\n大学物理7.4.46.在复色光照射下的单缝衍射图样中,其中某一未知波长光的第三级明纹极大位置恰与波长为λ=600nm光的第二级明纹极大位置重合,求这种光波的波长。解:λ′λ′asinθ=(2k′+1)=(2×3+1)22λλasinθ=(2k+1)=(2×2+1)2255λ′=λ=×600=428.6(nm)77完\n大学物理7.4.5某种单色平行光垂直入射在单缝上,单缝宽a=0.15mm.缝后放一个焦距f=400mm的凸透镜,在透镜的焦平面上,测得中央明条纹两侧的两个第三级暗条纹之间的距离为8.0mm,求入射光的波长.解:设第三级暗纹在θ3处x3asinθ=3λ3此暗纹到中心的距离为x=ftgθ≈=fsinθ333fλΔx=kx≈3faλa3两侧第三级暗纹的距离是26xfam==λ8.0m3λ==(2)x3af680.15/6400×(×)=500nm\n大学物理7.4.6光栅宽为2cm,共有6000条缝。如果用钠光(589.3nm)垂直照射,在哪些角度出现光强极大?−22.0×101−5解:a+b==×10(m)60003由光栅方程(a+b)sinθ=kλ(k=0,±1,±2,L)−9=k×0.1770λ589.3×10sinθk=k=k×−5a+b10/3k=0,sinθ=0,θ=000k=±1,sinθ=±1×0.1770,θ=±11°12′′11k=±2,sinθ=±2×0.1770,θ=±20°44′′22k=±3,sinθ=±3×0.1770,θ=±32°4′′33k=±4,sinθ=±4×0.1770,θ=±45°4′′44k=±5,sinθ=±5×0.1770,θ=±62°15′′55\n大学物理7.4.7某单色光垂直入射到一厘米刻有6000条刻线的光栅上。如果第一级谱线的偏角为20o,试问入射光的波长如何?它的第二级谱线将在何处?1−6解:此光栅常数为ab+=cm=1.6710×m6000光栅方程()ab+sinθ=kλ−2o()ab+×sin1θ0sin20−7λ===5.710×mn=570mk60001×kk′′λoo2sinθ′==sin20=×=sin200.683abk+1°θ=435′