大学物理期中复习new

大学物理期中复习new

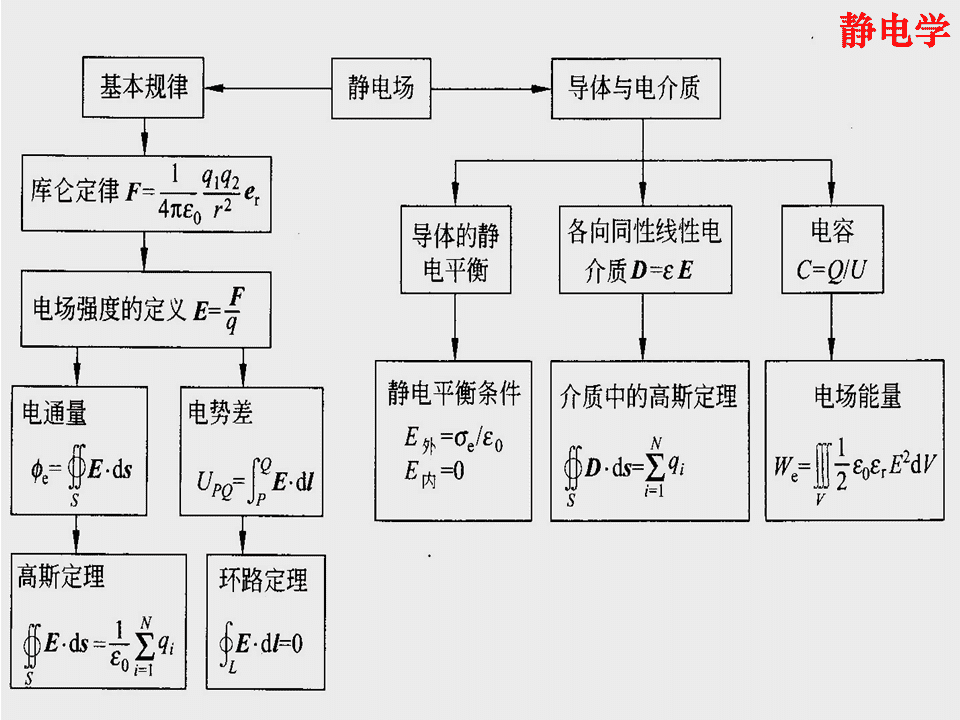
大学物理（C）集体复习课2012.4.8\n静电学\n一、知识点：描述静电场性质的两个物理量：电场强度、电势关于静电场的两个基本定理：高斯定理、环路定理1.电场强度F(1)定义式E单位正电荷所受到的电场力q01qq0(2)真空中点电荷的库仑定律Fe2r4r0q点电荷q产生的电场强度Ee2r4r0\n(3)电场强度的叠加原理1qidqEEi2eriE2er矢量叠加ii4πε0ri40r\n\n(4)电场线及电通量：在电场中穿过任意曲面S的电场线条数ΦdΦEdSeeSS穿出为正对闭合曲面ΦEdS取面元外法线方向eS穿入为负(5)静电场的高斯定理1源自正电荷ΦeSEdSq内E有源场汇于负电荷00总场强的通量Ф=0，E是曲面上的总场强，由所有电荷产生e用高斯定理求电场强度一般要求电荷(电场)分布具有对称性\n2.电势E0无旋场(1)静电场是保守场LEdl0静电场的环路定理"0"(2)电势能q0在电场E中某点a的电势能：Waq0Edla对无限大、无限长带电体，电势能零点不能选在无限远W"0"a(3)电势定义VEdl←已知场强分布aqa0b对路径积分(4)电势差UVVEdlababa\nq(5)点电荷电场中某点的电势Va4r0nqdqi(6)电势叠加原理VaVa代数和i140riQ4r0(7)计算电势的两种方法已知电荷分布↑对带电体积分\n3.E、V的关系(1)等势面与电场线处处正交、沿电场线方向电势降低(2)电场强度与电势的微分关系EVVVV在直角坐标系中EEExyzxyz\n4.电偶极子（ElectricDipole）等量异号电荷+q、-q，相距为lqql理想模型：所求场点到电偶极子中心的距离r>>l电偶极矩：pql方向：从-q指向+q•处在均匀电场中的电偶极子：力矩MpE电势能EpEθ=0时稳定平衡p\n二、典型问题：库仑定律+场强叠加原理电场强度的计算高斯定理+对称性电势梯度的负值电通量的计算电势定义电势的计算电势叠加原理电场力及做功\n★电场强度的计算一些常见均匀带电体的电场强度：Q点电荷、均匀带电球面(体)外E24πr0无限长均匀带电直线、圆柱面(体)外E2εr0\n均匀带电球面内、无限长均匀带电圆柱面内E0Qrr均匀带电球体内E34πR300rr无限长均匀带电圆柱体内E222R00\n无限大均匀带电平面E20匀强电场平行板电容器板间E0半无限长均匀带电直导线=ˆˆEij44xx00\nRλ一段均匀带电圆弧的圆心处EsinθO2R0θ圆环(圆盘)中心、无限大平面上E0半圆弧+两根半无限长直线，圆心O处λROE0O\n叠加原理直导线柱面柱体点电荷圆环圆盘大平板厚板补偿法球面球体\n\n\n\n\n\n例4：设半径为R的球体，电荷体密度为ρ=kr，k为常量，求：电场强度分布。分析：ρ随半径变化，非均匀带电球体，但r相同处ρ相同，电荷(电场)仍为球对称分布，可用高斯定理。解：做半径为r的同心球面为高斯面，由于对称性，高斯面上场强大小处处相同，方向沿径向，其电通量：122dVEd4SrEkrdV4rdrSV04RkR24Eeˆ球体外(r>R)：dVkr4rdrkR2rV04r0rkr234球体内(rR)：RRkr4rdr24kkRˆˆ3ˆEdEerdree0022rr2r44rrr000kkrr2球体内(r>R2-R1平行板电容器RR21②若R→孤立导体球22L•柱形电容器C若R>>R-R平行板电容器121ln(RR)21\n(2)电容器的并联每个电容器两端的电势差相等CCi并联使总电容增大，可以提高容量(3)电容器的串联每个电容器极板所带的电量相等11等效电容小于任何一个电容器的电容CCi串联可以提高耐压能力\n电场能量2Q112电容器的储能WCeUQUU:电势差22C212电场能量密度wEe2任意电场能量的计算12WWEddV对电场存在的空间积分V:体积eeVV21WVedq对带电体的积分V:电势2Q\n典型问题导体的静电感应电容的计算电容器的储能公式电场能量场强对空间的积分电势对带电体的积分\n例：如图，接地导体球附近有一点电荷q,相距l求：导体上感应电荷的电量l解：设感应电量为q′R感应电荷分布在球面上，但不均匀oq接地→U=0，球心的电势为0←等势体任取球面上一块电荷元dq，其在球心处的电势为dqdqqdU球面在球心的电势U140R4400RRqqR球心总电势U0qq040R4ll0接地意味着导体电势为零，不意味着电荷为零q球外没有其他带电体时U0q04R0\n例：两个相距很远的导体球，半径分别为a、b(

查看更多