大学物理总复习总结

大学物理总复习总结

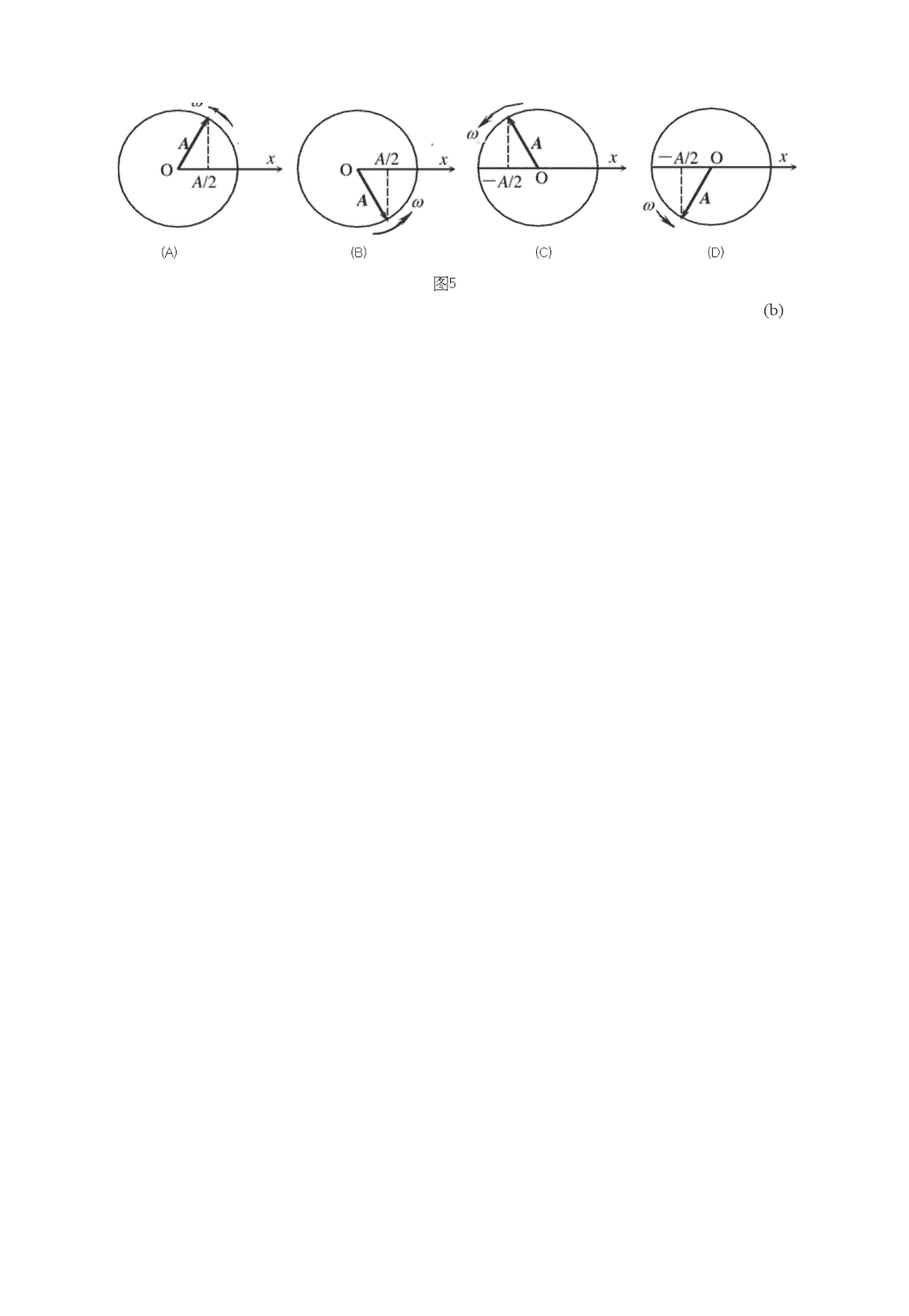
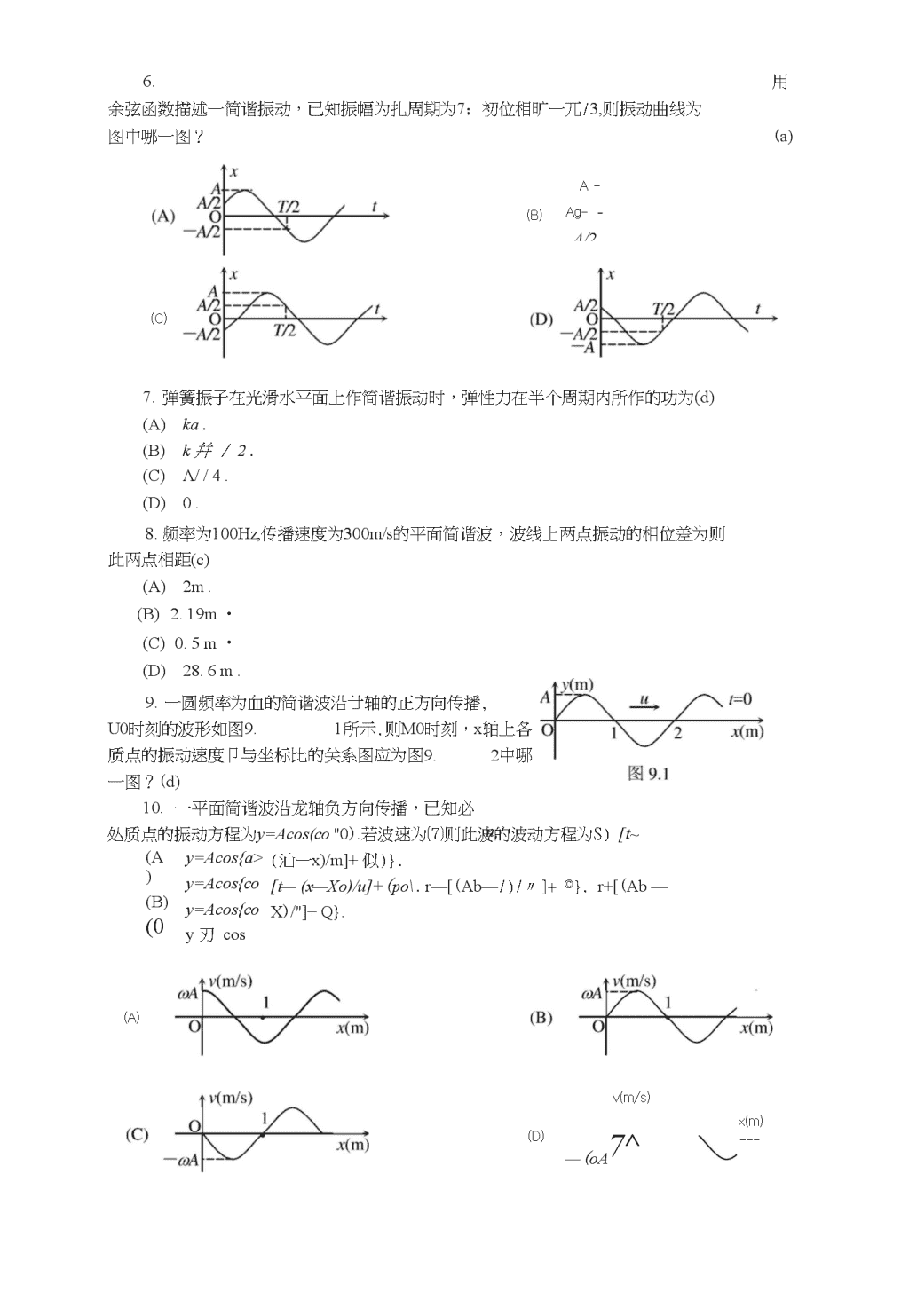
第二部分(机械振动与机械波、相对论)一.选择题1.一质点作简谐振动，振动方程为A=Acos(69t+初，当时间t=T/2(7为周期)时，质点的速度为(A)-Acosin(p.(C)-Acocoscp.(B)Acosin(p.(D)Acocos(p.(b)2.把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度然后由静止放手任其振动，从放手吋开始计吋，若用余弦函数表示其运动方程，则该单摆振动的初位相为(A)&.(C)0.(D);z/2.(c)3.两个质点各自作简谐振动，它们的振幅相同、周期相同，第一个质点的振动方程为孟二尿os(et+a).当第一个质点从相对平衡位置的正位移处回到平衡位置吋，第二个质点正在最大位移处，则第二个质点的振动方程为⑷⑻(0(D)x?=Acos(coX2=Acos(qX2=/Icos(QX2=t4cost+a+龙/2).t+a-V2)・a—3tt/2).t+a+tt).(b)4.轻弹簧上端固定，下系一质量为血的物体，稳定后在nK的下边又系一质量为饥的物体,于是弹簧又伸长了△X,若将血移去，并令其振动，则振动周期为(A)炮&华.V"g(B)T丸&巨丕.V他g(C)T=—.(b)2ttV加2gzn\T_n/(D)欣时而硕-5•—个质点作简谐振动，振辐为A,在起始时刻质点的位移为A/2,且向/轴的正方向运动，代表此简谐振动的旋转矢量图为图5中哪一图?\n(A)(B)(C)(D)图5(b)\n6.用余弦函数描述一简谐振动，已知振幅为扎周期为7；初位相旷一兀/3,则振动曲线为图中哪一图？(a)(C)(B)A-Ag--A/27.弹簧振子在光滑水平面上作简谐振动时，弹性力在半个周期内所作的功为(d)(A)ka.(B)k幷/2.(C)A//4.(D)0.8.频率为100Hz,传播速度为300m/s的平面简谐波，波线上两点振动的相位差为则此两点相距(c)(A)2m.(B)2.19m・(C)0.5m・(D)28.6m.9.一圆频率为血的简谐波沿廿轴的正方向传播,U0时刻的波形如图9.1所示.则M0时刻，x轴上各质点的振动速度卩与坐标比的关系图应为图9.2中哪一图？(d)10.一平面简谐波沿龙轴负方向传播，已知必处质点的振动方程为y=Acos(co"0).若波速为⑺则此波的波动方程为S)[t~(汕一x)/m]+似)}.[t—(x—Xo)/u]+(po\.r—[(Ab—/)/〃]+©}.r+[(Ab—X)/"]+Q}.(A)(B)(0(D)y=Acos{a>y=Acos{coy=Acos{coy刃cos(A)u,v(m/s)(D)—(oA7^x(m)►\n图9.26.如图11.1所示为一平面简谐波在t=0时刻的波形图，该波的波速尸200m/s,则\nP处质点的振动曲线为图11・2小哪一图所画出的曲线？(C)(C)(A)yp(m)(B)(D)11.212、一平面简谐波，波速沪5m•s-1.t=3吋波形曲线如图12.则尸0处的振动方程为(a)⑷尸2X10—Los(庆/2—加2)(SI).(B)产2XlO^cos(加+龙)(SI).(C)J^2XIOCCOS(^f/2W2)(SI).(D)y-2X10"2cos(^-3^/2)(SI).13、一列机械横波在十时刻的波形曲线如图13所示，则该吋刻能量为最大值的媒质质元的位置是：(b)⑷oz,b,d,f⑻a,c,e,g(C)o',d.(D)b,f.14、一平血简谐波在弹性媒质中传播，在某一瞬吋,媒质屮某质元正处于平衡位置，此吋它的能量是(c)(A)动能为零，势能最大.(B)动能为零,势能为零.(0动能最大，势能最大.(D)动能最大，势能为零・15、如图15所示为一平面简谐机械波在十吋刻的波形曲线.若此吋A点处媒质质元的振动动能在增大，贝9(b)(A)A点处质元的弹性势能在减小.(B)波沿x轴负方向传播.(C)B点处质元的振动动能在减小.(D)各点的波的能量密度都不随吋间变化.16、如图16所示，两相干波源SI和卩相距2/4(A为波长)，S］的位相比S2的位相超前必，在弘S2的连线上,SI外侧各点(例如P点)两波引起的两谐振动的位相差是(b)\n(A)0.Sis2图16(B)n.-P(C)兀/2.(D)3刃2.17、在波长为久的驻波屮，两个相邻波腹Z间的距离为(b)(A)2/4.(B)2/2.(C)3A/4.(D)A18、.一机车汽笛频率为750Hz,机车以时速90公里远离静止的观察者，观察者听到声音的频率是(设空气屮声速为340m/s):(b)(A)810Hz.(B)699Hz.(C)805Hz.(D)695Hz19、用余弦函数描述一简谐振子的振动，若其速度一时间(卩一广)关系曲线如图19所示,图19则振动的初相位为(A)(A)7T/6.⑻7T/3.(0龙/2.(D)2兀/3.20、一质点作简谐振动,周期为7；质点由平衡位置向x轴正方向运动时，由平衡位置到二分之一最大位移这段路程所需要的时间为(B)(A)〃4.(B)7/12.(C)T/6.(D)T/8.21、一平面简谐波在弹性媒质中传播,在媒质质元从最大位移处冋到平衡位置的过程中(C)(A)它的势能转换成动能.(B)它的动能转换成势能.(0它从相邻的一段媒质质元获得能量，其能量逐渐增加.(A)它把自己的能量传给相邻的一段媒质质元，其能量逐渐减小.21一简谐振动曲线如图所示.则振动周期是(A)2.62s.(b)(B)2.40s.(C)2.20s.\n(A)2.00s\n22、已知某简谐振动的振动曲线如图所示，位移的单位为厘米，时间单位为秒.则此简谐振动的振动方程为：c()(A)兀=2cos谆皿+舟兀)•(B)x=2cos(-^7ir--|7i).(C)x=2cos(^7l/+^7l)•23y=0.1cos(37ir—7LT+71)(SI),t形曲线如图所示，则(c)。点的振幅为-0.1-平面简谐波的表(A)m.(0(D)波长为3自、方两点间相位差为兀/2・波速为9m/s•m.(0)x=2cos(^7tr-^K).(ST)(ST)v二、填空题1、用40"的力拉一轻弹簧，可使其伸长20cm,此弹簧下应挂kg的物体，才能使弹簧振子作简谐振动的周期徉0.2亦•2、一质点沿/轴作简谐振动，振动范围的中心点为x轴的原点.己知周期为7；振幅为A⑴若Z=0时质点过x=0处且朝/轴正方向运动,则振动方程为尸Acos{27rt/T-7i/fi);⑵若t=0吋质点处于x=A/2处且朝x轴负方向运动，则振动方程为a=_Joos(2^/?t-^/3).\n8、一列平面简谐波沿x轴正方向无衰减地传播，波的振幅为2X10-3m,周期为0.01s,波速为400m/s,当Z=0时x轴原点处的质元正通过平衡位置向y轴正方向运动，则该简谐波的表达式为y=2X10_3cos（200欣-空/2-;z/2）..9、相对于空气为静止的声源振动频率为人，接收器R以速率w远离声源，设声波在空气中传播速度为u,那么接收器收到的声波频率％二vAu-v^/u.1n10、如图10所示，一平面简谐波沿0/轴负方向传播，波长为入若P处质点的振动方程是并二Mcos（2/rvf+龙/2）.则该波的波动方程是_-2滋/1+0・；11、质量为刃物体和一个轻弹簧组成弹簧振子，其固有振动周期为7：当它作振幅为/!口由简谐振动时，其振动能量E二27t2mA2/T212、一物体同时参与同一直线上的两个简谐振动：12X]=0.05cos（4兀/+-兀）（SI）,x2=0.03cos（4;tr——兀）（SI）合成振动的振幅为13、、一平血简谐波沿"轴正方向传播，波速u二r二0时刻的波形曲线如图所示.可知波长二m；振幅A=0.2m频率二—125Hz33m.y(m)0.0214、一列火车以20m/s的速度行驶，若机车汽笛的频637.5Hz率为600Hz,一静止观测者在机车前和机车后所听到的声音频率分别为和_、566.7Hz（设空气中声速为340m/s）.15、狭义相对论的两个基本假设分别是相对性原理，和光速不变原理16、在S系屮观察到两个事件同时发生在x轴上，其间距离是1/〃。在S'系屮观察这两个事件之间的距离是2/〃。则在S'系中这两个事件的时间间隔是—-0.577X10（17—宇航员要到离地球为5光年的星球去旅行，如果宇航员希望把这路程缩短为3光年,真空中光速用Q表示，则他所乘的火箭相对地球的速度应是0.8c18、在某地发生两件事，静止位于该地的甲测得时间间隔为4s,若相对甲做匀速直线运动的乙测得时间间隔为5s,真空中光速用c表示，则乙相对于甲的运三、计算题1、一质点同时参与两个同方向的简谐振动，其振动方程分别为(ST)Xi=5X10：cos(4f+^/3)A2=3X102sin(4r—龙/6)(ST)\n画出两振动的旋转矢量图，并求合成振动的振动方程.因A2=3X10_2sin(41—^/6)=3X10'cos(4f-^/6-^/2)=3X10_2cos(4f-2^/3)=-3X10一Los(4f+^/3)所以合振动的振动方程为X=X\+X2co\n=5X10_2cos(4方+龙/3)-3X102cos(4t+^/3)=2X10_2cos(4^+^/3)(SI)2、某质点作简谐振动,周期为2s,振幅为0.06m,开始计时(片0)时，质点恰好处在负向最大位移处，求(1)该质点的振动方程；(2)此振动以速度^2m/s沿x轴正方向传播吋，形成的一维简谐波的波动方程(3)该波的波长.解：(1)取该质点为坐标原点0.t=0时刻yo=Acos(/)b=-Avo=-Aa)sin炉=0得心.所以振动方程为yo=O.06cos(2^-广/2+龙)二0.06cos(龙纤龙)(ST)(2)波动方程为y=0.06cos［龙(t-xAl)+/r］=0.06cos［兀(t-x/i)A,=u7=4(m)3、如图4,两列相干波在P点相遇，一列波在B点引起的振动是yio=3X103cos2^-f(SI)另一列波在C点引起在振动是720=3X103cos(2^-f+^/2)(SI)BP二0.45m,CP=0.30m,两波的传播速度u=0.20m/s,不考虑传播屮振幅的减小，求P点合振动的振动方稈.两列相干波在P点引起的振动分别是yi=3X10_cos[2兀(t-l\/u)]=3X10_3cos(2讥-9分2)=3XlO^cos(2庆-分2)j2=3X10~3cos[2^-(t-h/u)+兀/2]=3X10~3cos(2^f-3^+^/2)=3X10~3cos(2^f-^/2)所以合振动方程为y=yi+y->=6X10~cos(2^Z-^/2)(SI)4、图示一平面余弦波在t=0时刻与t=2s时刻的波形图.已知波速为u,求\n(1)坐标原点处介质质点的振动方程；y(m)(2)该波的波动表达式.解：(1)比较t=0吋刻波形图与t=2s吋刻波形图，可知此波向左传播.在t=0时刻，0处质点0=Ac0,0<--A69sin0,故0=-7r/2又t二2s,0处质点位移为A/4^=Acos(47rv-7t/2)-n/4=47tv-n/2所以1,v=—Hz16振动方程为Vo=Acos(7rr/8-7r/2)(ST)(2)波速u=20/2m/s=10m/s波长二160m波动表达式tX1y=Acos[271(—+—)--71]1616025、图示一平面简谐波在t=0时刻的波形图，求(1)该波的波动表达式；(2)P处质点的振动方程.解：(1)。处质点，十二0时y0=Acos0=0,=-Acosin0>0所以(/)——n/2又T=2/w=5s故波动表达式为fYITy=0.04cos[2tt(-(SI)50.42(2)户处质点的振动方程为=0.04cos[2k(|一焉)一专]二O-048s(0.4皿一乎)6、一平面简谐波沿血轴正方向传播，波的表达式为y=Acos2ji(vt-x/Z),而另一平面简谐波沿％轴负方向传播，波的表达式为y=2Acos2兀(M+x/zl)求：(1)A/4处介质质点的合振动方程；(2)x-X/4处介质质点的速度表达式.解：⑴x=A/4处：y{=Acos(2兀必一兀/2),y2=2Acos(2兀vT+tt/2))*.*yi,乃反相合振动振幅As=2A—A=A,且合振动的初相和力的初相一样为兀/2.Asin(p、+A.sin(p、-A,+A,tg(p0=!=———=—!"£cos®+舛cos(p20合振动方程y=Acos(27rW+7r/2)\n(2)jt=2/4处质点的速度v=d>7dr=一2兀Msin(2兀vr+tt/2)=2兀m4cos(2兀w+7t)7、在S系中观察到两个事件同时发生在x轴上，其间距是1000mo在S，系中测得两事件的发生地点相距2000m。试求在S'系中这两事件的时间间隔。解：假设系中长度为原长，利用长度的相对论变化公式，可得:v=c27b(V

查看更多