- 2022-08-16 发布 |
- 37.5 KB |
- 77页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理波动光学
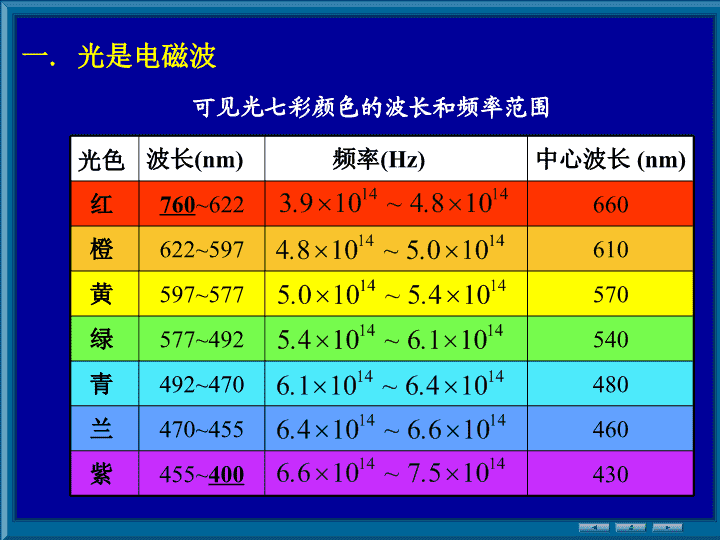
第13章波动光学基础波动光学知识结构光的干涉研究光的波动现象及规律光的衍射光的偏振光的波动特征光的波动特征横波特征\n一.光是电磁波光色波长(nm)频率(Hz)中心波长(nm)红760~622660橙622~597610黄597~577570绿577~492540青492~470480兰470~455460紫455~400430可见光七彩颜色的波长和频率范围\n(1)相长干涉(明)(2)相消干涉(暗)二.相干叠加如果如果相干条件:(1)频率相同(2)相位差恒定(3)光矢量振动方向平行相干光源:同一原子的同一次发光三.相干条件、相干光源\n§13.3获得相干光的方法杨氏实验(分波阵面法)一.杨氏实验明条纹位置明条纹位置明条纹位置获得相干光的方法1.分波阵面法(杨氏实验)2.分振幅法(薄膜干涉)•实验现象(同一原子的同一次发光)\n•理论分析相长干涉(加强、明纹)相消干涉(暗纹)(级数)(条纹中心坐标)很小\n(1)屏上相邻明条纹中心或相邻暗条纹中心间距为一系列平行的明暗相间条纹(4)当用白光作为光源时,在零级白色中央条纹两边对称地排列着几条彩色条纹Ik012-1-24I0x0x1x2x-2x-1光强分布讨论(2)已知d,D及Δx,可测(3)Δx正比,D;反比d•(5)当把暗纹条件写成时,d=0,k=0\n二.洛埃镜(洛埃镜实验结果与杨氏双缝干涉相似)接触处,屏上O点出现暗条纹半波损失有半波损失相当于入射波与反射波之间附加了一个半波长的波程差无半波损失入射波反射波透射波透射波没有半波损失••计算方法同双缝实验,但仅在直射光和反射光相遇区域出现干涉条纹.•\n(1)相邻明纹间距分别为(2)双缝间距d为13.2.双缝干涉实验中,用钠光灯作单色光源,其波长为589.3nm,屏与双缝的距离D=600mm解例求(1)d=1.0mm和d=10mm,两种情况相邻明条纹间距分别为多大?(2)若相邻条纹的最小分辨距离为0.065mm,能分清干涉条纹的双缝间距d最大是多少?\n13.3.用白光作光源观察杨氏双缝干涉。设缝间距为d,缝面与屏距离为D解最先发生重叠的是某一级次的红光和高一级次的紫光清晰的可见光谱只有一级例在400~760nm范围内,明纹条件为求能观察到的清晰可见光谱的级次\n§13.4光程与光程差若时间t内光波在介质中传播的路程为r,则相应在真空中传播的路程应为光程是一个折合量,在相位改变相同的条件下,把光在介质中传播的路程折合为光在真空中传播的相应路程改变相同相位的条件下真空中光波长光程\n由光程差计算物象之间等光程原理光程1光程2光程3光程1=光程2=光程3相位差光程……多种介质真空中光波长光程差结论:透镜不造成附加光程差\n用折射率n=1.58的很薄的云母片覆盖在双缝实验中的一条缝上,这时屏上的第七级亮条纹移到原来的零级亮条纹的位置上。如果入射光波长为550nm解设云母片厚度为d。无云母片时,零级亮纹在屏上P点,则到达P点的两束光的光程差为零。加上云母片后,到达P点的两光束的光程差为当P点为第七级明纹位置时例求此云母片的厚度是多少?条纹上移还是下移?光程差d=0\n§13.5薄膜干涉一.等厚干涉(薄膜厚度不均匀)反射光2反射光1·S12(分振幅法)两条光线的光程差\n1考虑半波损失讨论(1).加强时,(2).透射光无半波损失2.无半波损失干涉相长干涉相消干涉相长干涉相消\n5.光线垂直入射反射光1反射光2入射光3.同一厚度d对应同一级条纹——等厚条纹4.把一束光“分割”——分振幅法8.注意区分“条纹级数k”与“条纹序数(第几条)”\n两相邻明条纹(或暗条纹)对应的厚度差都等于若为空气层时,相邻明条纹(或暗条纹)对应的厚度差\n1.劈尖干涉等厚条纹待测工件平晶光垂直入射时,两相邻条纹对应的空气层厚度差都等于相邻条纹之间距adkdk+1明纹中心暗纹中心讨论(1)空气劈尖顶点处是一暗纹(2)可测量小角度θ、微位移x、微小直径D、波长l等为什么θ要小?(3)测表面不平整度\n2.牛顿环光程差明纹暗纹\n(1)测透镜球面的半径R已知,测m、rk+m、rk,可得R(2)测波长l已知R,测出m、rk+m、rk,可得l(3)检测透镜的曲率半径误差及其表面平整度(5)若接触良好,中央为暗纹——半波损失,条纹从中央算起。样板待测透镜条纹半径讨论(6)条纹间距(外圆纹的级次比内圆纹的级次高)\n13.7.为了测量一根细的金属丝直径D,按图办法形成空气劈尖,用单色光照射形成等厚干涉条纹,用读数显微镜测出干涉明条纹的间距,就可以算出D。已知单色光波长为589.3nm,测量结果是:金属丝与劈尖顶点距离L=28.880mm,第1条明条纹到第31条明条纹的距离为4.295mm解由题知直径例求金属丝直径DD\n一平面单色光波垂直照射在厚度均匀的薄油膜上,油膜覆盖在玻璃板上,所用光源波长可连续变化,观察到500nm和700nm这两个波长的光在反射中消失。油的折射率为1.30,玻璃的折射率为1.50解根据题意,不需考虑半波损失(),暗纹的条件为例求油膜的厚度\n二.等倾干涉(薄膜厚度均匀)两条光线的光程差考虑到有半波损失\n(1)等倾干涉条纹为一系列同心圆环;内疏外密;内圆纹的级次比外圆纹的级次高条纹特点(2)膜厚变化时,条纹发生移动。当薄膜厚度增大时,圆纹从中心冒出,并向外扩张,条纹变密E\n13.10.波长550nm黄绿光对人眼和照像底片最敏感。要使照像机对此波长反射小,可在照像机镜头上镀一层氟化镁MgF2薄膜,已知氟化镁的折射率n=1.38,玻璃的折射率n=1.55.解两条反射光干涉减弱条件增透膜的最小厚度增反膜薄膜光学厚度(nd)仍可以为例但膜层折射率n比玻璃的折射率大求氟化镁薄膜的最小厚度说明\n§13.6迈克耳逊干涉仪一.干涉仪结构二.工作原理光束1和2发生干涉d加强减弱光程差(无半波损失)(有半波损失)\n2.若M1、M'2有小夹角3.若M1平移d时,干涉条纹移过N条,则有当M1和M'2不平行,且光平行入射,此时为等厚条纹1.若M1、M2平行三.条纹特点等倾条纹\n四.应用1.微小位移测量3.测折射率2.测波长\n§13.7惠更斯—菲涅耳原理一.光的衍射现象1.现象衍射屏观察屏2.衍射光在传播过程中绕过障碍物的边缘而偏离直线传播的现象衍射现象是否明显取决于障碍物线度与波长的对比,波长越大,障碍物越小,衍射越明显。说明光源(剃须刀边缘衍射)\n二.惠更斯—菲涅耳原理同一波前上的各点发出的都是相干次波。设初相为零,面积为s的波面Q,其上面元ds在P点引起的振动为各次波在空间某点的相干叠加,就决定了该点波的强度。1.原理内容2.原理数学表达取决于波面上ds处的波强度,为倾斜因子.••\nP处波的强度说明(1)对于一般衍射问题,用积分计算相当复杂,实际中常用半波带法和振幅矢量法分析。(2)惠更斯—菲涅耳原理在惠更斯原理的基础上给出了次波源在传播过程中的振幅变化及位相关系。(原方向传播)(不能反向传播)\n(远场衍射)2.夫琅禾费衍射(近场衍射)1.菲涅耳衍射三.光的衍射分类无限远光源无限远相遇光源O,观察屏E(或二者之一)到衍射物S的距离为有限的衍射,如图所示。光源O,观察屏E到衍射物S的距离均为无穷远的衍射,如图所示。(菲涅耳衍射)(夫琅禾费衍射)\n·*§13.8单缝的夫琅禾费衍射一.典型装置(单缝夫琅禾费衍射典型装置)的光程差二.菲涅耳半波带法★1.衍射暗纹、明纹条件——中央明纹•(a为缝AB的宽度)\n此时缝分为两个“半波带”,P为暗纹。暗纹条件半波带半波带P为明纹。此时缝分成三个“半波带”,明纹条件••λ|2λ|2λ|2λ|2λ|2λ|2λ|2λ|2λ|2\n(1)得到的暗纹和中央明纹位置精确,其它明纹位置只是近似。(2)单缝衍射和双缝干涉条纹比较。单缝衍射条纹双缝干涉条纹说明\n2.单缝衍射明纹角宽度和线宽度衍射屏透镜观测屏中央明纹角宽度线宽度角宽度相邻两暗纹中心对应的衍射角之差线宽度观察屏上相邻两暗纹中心的间距第k级明纹角宽度请写出线宽度\n(1)波长越长,缝宽越小,条纹宽度越宽。波动光学退化到几何光学。观察屏上不出现暗纹。讨论(2)(4)缝位置变化不影响条纹位置分布(3)(单缝夫琅禾费衍射典型装置)·\n求对于暗纹有则如图示,设有一波长为的单色平面波沿着与缝平面的法线成角的方向入射到宽为a的单缝AB上。解在狭缝两个边缘处,衍射角为的两光的光程差为例写出各级暗条纹对应的衍射角所满足的条件。\n13.14解(1)中央明纹宽度例af(2)第一级明纹宽度\n四.光学仪器的分辨本领1.圆孔的夫琅禾费衍射孔径为D衍射屏中央亮斑(爱里斑)2.透镜的分辩本领几何光学物点相对光强曲线经圆孔衍射后,一个点光源对应一个爱里斑波动光学物点一一对应像点一一对应像斑爱里斑的半角宽度为\n瑞利判据:对于两个等光强的非相干物点,如果一个像斑中心恰好落在另一像斑的边缘(第一暗纹处),则此两像被认为是刚好能分辨。此时两像斑中心角距离为最小分辨角可分辨刚可分辨不可分辨分辨率\n眼睛的最小分辨角为设人离车的距离为S时,恰能分辨这两盏灯。取在迎面驶来的汽车上,两盏前灯相距120cm,设夜间人眼瞳孔直径为5.0mm,入射光波为550nm。例人在离汽车多远的地方,眼睛恰能分辨这两盏灯?求解d=120cmS由题意有观察者\n一.衍射光栅1.光栅反射光栅透射光栅透光宽度不透光宽度2.光栅常数d—大量等宽等间距的平行狭缝(或反射面)构成的光学元件光栅宽度为l,每毫米缝数为m,则总缝数§13.9衍射光栅及光栅光谱\n只考虑单缝衍射强度分布只考虑双缝干涉强度分布双缝光栅强度分布3.光栅衍射的基本特点屏上的强度为单缝衍射和缝间干涉的共同结果。以二缝光栅为例结论:\n二.多缝干涉1.五缝干涉例子主极大角位置条件k称为主极大级数相邻两缝在P点引起的光振动相位差为主极大强度为主极大条件下单缝在P点引起光振动矢量的振幅\n暗纹条件各缝光振幅矢量:相邻矢量相位差:暗纹条件(1)对五缝干涉,相邻两主极大间有4个极小,3个次极大。结论-6-5-4-3-2-10+1+2+3+4+5+6I/I(2)主极大光强是相应位置处单缝引起光强的52倍。k\n对N缝干涉两主极大间有N-1个极小,N-2个次极大。衍射屏上总能量主极大的强度由能量守恒,主极大的宽度随着N的增大,主极大变得更为尖锐,且主极大间为暗背景2.N缝干涉缝干涉强度分布缝干涉强度分布缝干涉强度分布\n三.光栅的夫琅禾费衍射1.单缝衍射和缝间干涉的共同结果几种缝的光栅衍射\n缝间干涉主极大就是光栅衍射主极大,其位置满足—光栅方程多缝干涉主极大光强受单缝衍射光强调制,使得主极大光强大小不同,在单缝衍射光强极小处的主极大缺级。缺级条件如缺级缺级3.缺级条件分析2.光栅方程同时满足\n4.暗纹条件设光栅总缝数为N,各缝在观察屏上某点P引起的光振动矢量为为相邻光振动矢量夹角暗纹条件光栅衍射中,两主极大条纹之间分布着一些暗纹,这是缝间干涉相消而成。当这些振动矢量组成的多边形封闭时,合矢量为零,对应点为暗纹,则其中\n设光栅常数为d,总缝数为N的光栅,当入射光波长为时,分析其夫琅禾费衍射主极大条纹角宽度与N的关系。第k级主极大相邻的两暗纹有N越大,主极大角宽度越小,条纹越细。例解暗纹位置满足条件第k级主极大角宽度\n四.光栅光谱及分辨本领1.光栅光谱0级1级2级-2级-1级3级-3级白光的光栅光谱2.光栅的色分辨本领(将波长相差很小的两个波长和+分开的能力)色谱仪的色分辨率重叠按波长排列\n设两波长1和2=1+在第k级刚好能被光栅分辨,则有根据瑞利判据:当(光栅的色分辨本领)由(1)、(2)得时刚能分辨其中为波长1第k级主极大半角宽度,且光栅的色分辨率(不要求)讨论增大主极大级次k和总缝数N,可提高光栅的分辨率。\n五.斜入射的光栅方程主极大条件k=0,1,2,3…缺级条件最多明条纹数p(N与正入射相同,但可观测的条纹最高级次增大)\n当=-90o时当=90o时一束波长为480nm的单色平行光,照射在每毫米内有600条刻痕的平面透射光栅上。求(1)光线垂直入射时,最多能看到第几级光谱?(2)光线以30o入射角入射时,最多能看到第几级光谱?例解(1)(2)(3.47取整)\n(2)斜入射时,可得到更高级次的光谱,提高分辨率。(1)斜入射级次分布不对称。(3)垂直入射和斜入射相比,完整级次数不变。(4)垂直入射和斜入射相比,缺级级次相同。上题中垂直入射级数斜入射级数说明\n时,第二级主极大也发生缺级,不符题意,舍去。每毫米均匀刻有100条线的光栅,宽度为D=10mm,当波长为500nm的平行光垂直入射时,第四级主极大谱线刚好消失,第二级主极大的光强不为0。(1)光栅狭缝可能的宽度;(2)第二级主极大的半角宽度。例(1)光栅常数第四级主极大缺级,故有求解时时,\n(2)光栅总的狭缝数设第二级主极大的衍射角为2N,与该主极大相邻的暗纹(第2N+1级或第2N-1级)衍射角为2N-1,由光栅方程及暗纹公式有代入数据后,得第二级主极大的半角宽度符合题意的缝宽有两个,分别是2.5×10-3mm和7.5×10-3mm\n一.线偏振光(平面偏振光)面对光的传播方向观察线偏振光可沿两个相互垂直的方向分解§13.10线偏振光自然光(光振动平行板面)(光振动垂直板面)线偏振光的表示法\n二.自然光面对光的传播方向观察自然光可用两个相互独立、没有固定相位关系、等振幅且振动方向相互垂直的线偏振光表示。自然光的表示法三.部分偏振光部分偏振光的分解部分偏振光部分偏振光可用两个相互独立、没有固定相位关系、不等振幅且振动方向相互垂直的线偏振光表示。\n部分偏振光的表示法平行板面的光振动较强垂直板面的光振动较强四.偏振度部分偏振光可看成是自然光和线偏振光的混合,设部分偏振光的强度为It,其中自然光强度为In,线偏振光的强度为Ip,则有线偏振光部分偏振光自然光偏振度\n§13.11偏振片的起偏和检偏马吕斯定律一.起偏和检偏自然光I0线偏振光I偏振化方向线偏振光I'二.马吕斯定律(马吕斯定律)—消光当;当起偏器检偏器\n检偏器检偏起偏器\n一束部分偏振光,当它通过一偏振片时,发现光强取决于偏振片的取向可以变化5倍。例解依题意得求此光的偏振度。\n平行放置两偏振片,使它们的偏振化方向成60夹角。让自然光垂直入射后,下列两种情况下:(1)无吸收时,有(1)两偏振片对光振动平行于其偏振化方向的光线均无吸收例求解(2)有吸收时,有(2)两偏振片对光振动平行于其偏振化方向的光线分别吸收了10%的能量透射光的光强与入射光的光强之比是多大?\n§13.12反射和折射产生的偏振布儒斯特定律一.反射和折射产生的偏振ib—布儒斯特角或起偏角自然光反射和折射后产生部分偏振光ib+γ=90o时,反射光为线偏振光二.布儒斯特定律线偏振光(相对折射率)\n玻璃片堆起偏和检偏玻璃片堆线偏振光例如n1=1.00(空气),n2=1.50(玻璃),则空气玻璃玻璃空气入射自然光\n13.19例解是布儒斯特角是布儒斯特角\n§13.13晶体的双折射现象方解石一.双折射现象(DoubleRefraction)1.双折射o光e光2.寻常光和非寻常光两折射光线中有一条始终在入射面内,并遵从折射定律,称为寻常光,简称o(ordinary)光另一条光一般不遵从折射定律,称非常光,简称e(extraordinary)光双折射现象一束光入射到各向异性的介质后出现两束折射光线的现象。\n双折射双折双折方解石晶体o光e光\n当方解石晶体旋转时,o光不动,e光围绕o光旋转\n3.晶体的光轴当光在晶体内沿某个特殊方向传播时不发生双折射,该方向称为晶体的光轴。例如方解石晶体(冰洲石)光轴光轴是一特殊的方向,凡平行于此方向的直线均为光轴。单轴晶体:只有一个光轴的晶体双轴晶体:有两个光轴的晶体4.主平面主平面晶体中光的传播方向与晶体光轴构成的平面.78o102o78o102o光轴与o光构成的平面叫o光主平面.光轴与e光构成的平面叫e光主平面.\n5.正晶体、负晶体e光光轴e光的主平面o光光轴o光的主平面··光轴在入射面时,o光主平面和e光主平面重合,此时o光振动和e光振动相互垂直。一般情况下,两个主平面夹角很小,故可认为o光振动和e光振动仍然相互垂直。光轴o光:e光:光轴(o光主折射率)(e光主折射率)(o光振动垂直o光主平面)(e光振动在e光主平面内)\n正晶体光轴光轴负晶体(垂直光轴截面)(垂直光轴截面)(平行光轴截面)(平行光轴截面)\no光二.单轴晶体中的波面(惠更斯作图法(ve>vo))方解石光轴2.光轴平行入射面,自然光垂直入射负晶体中方解石光轴1.光轴平行入射面,自然光斜入射负晶体中光轴e光o光e光e光o光光轴\n3.光轴平行晶体表面,自然光垂直入射此时,o,e光传播方向相同,但传播速度不同。从晶体出射后,二者产生相位差。\n三.晶体偏振器1.尼科耳棱镜2.渥拉斯顿棱镜上述两种棱镜得到的偏振光质量非常好,但棱镜本身价格很高,因而使用较少。负晶体o光o光e光加拿大树胶光轴\n出射o光e光的相差为3.波晶片自然光垂直入射波晶片后,o光,e光传播速度不同,产生的相位不同。波晶片(光轴平行于表面且厚度均匀的晶体)波晶片分类波片半波片全波片查看更多