大学物理(磁学)试卷
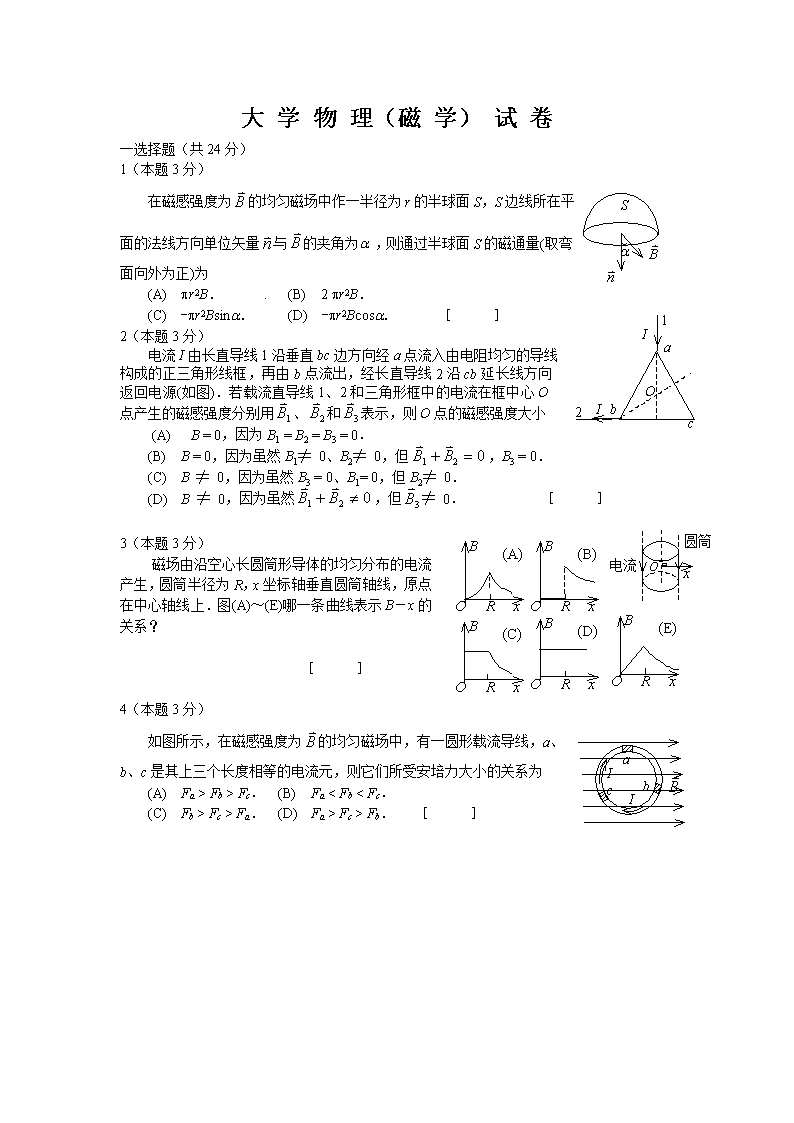
大学物理(磁学)试卷一选择题(共24分)1(本题3分)在磁感强度为的均匀磁场中作一半径为r的半球面S,S边线所在平面的法线方向单位矢量与的夹角为a,则通过半球面S的磁通量(取弯面向外为正)为(A)pr2B..(B)2pr2B.(C)-pr2Bsina.(D)-pr2Bcosa.[]2(本题3分)电流I由长直导线1沿垂直bc边方向经a点流入由电阻均匀的导线构成的正三角形线框,再由b点流出,经长直导线2沿cb延长线方向返回电源(如图).若载流直导线1、2和三角形框中的电流在框中心O点产生的磁感强度分别用、和表示,则O点的磁感强度大小(A)B=0,因为B1=B2=B3=0.(B)B=0,因为虽然B1≠0、B2≠0,但,B3=0.(C)B≠0,因为虽然B3=0、B1=0,但B2≠0.(D)B≠0,因为虽然,但≠0.[]3(本题3分)磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R,x坐标轴垂直圆筒轴线,原点在中心轴线上.图(A)~(E)哪一条曲线表示B-x的关系?[]4(本题3分)如图所示,在磁感强度为的均匀磁场中,有一圆形载流导线,a、b、c是其上三个长度相等的电流元,则它们所受安培力大小的关系为(A)Fa>Fb>Fc.(B)Fa
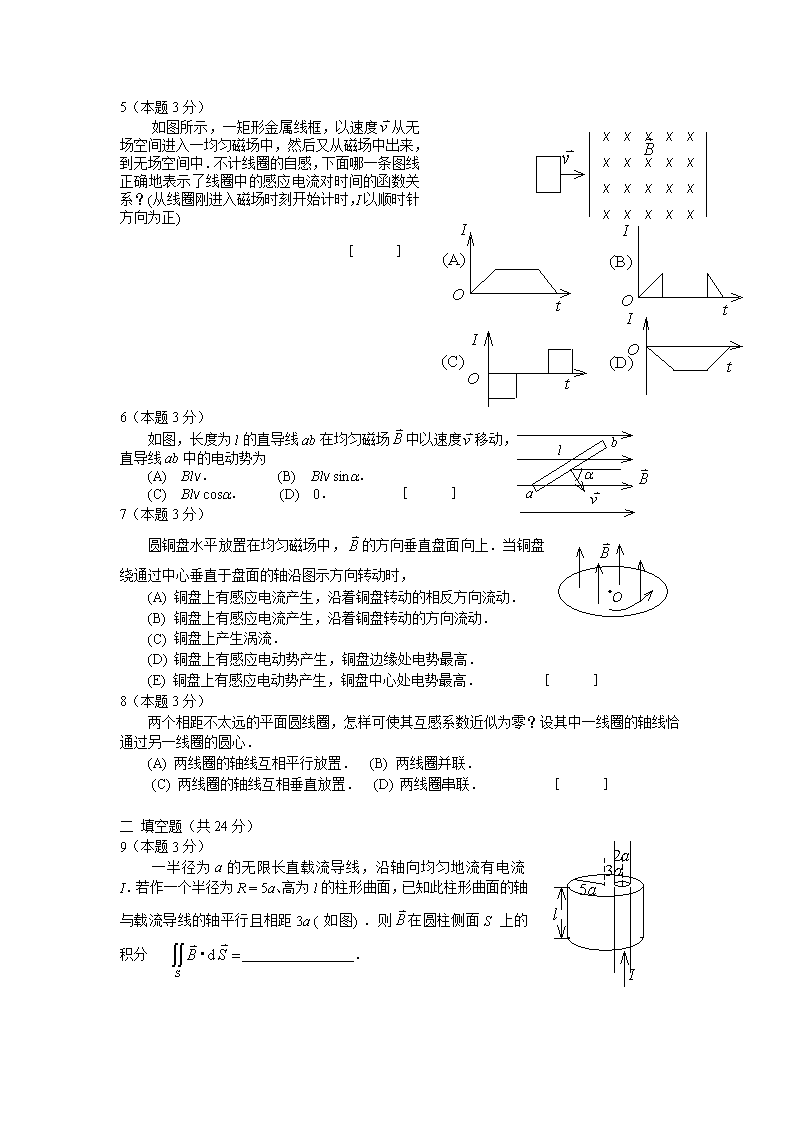
Fc>Fa.(D)Fa>Fc>Fb.[]\n5(本题3分)如图所示,一矩形金属线框,以速度从无场空间进入一均匀磁场中,然后又从磁场中出来,到无场空间中.不计线圈的自感,下面哪一条图线正确地表示了线圈中的感应电流对时间的函数关系?(从线圈刚进入磁场时刻开始计时,I以顺时针方向为正)[]6(本题3分)如图,长度为l的直导线ab在均匀磁场中以速度移动,直导线ab中的电动势为(A)Blv.(B)Blvsina.(C)Blvcosa.(D)0.[]7(本题3分)圆铜盘水平放置在均匀磁场中,的方向垂直盘面向上.当铜盘绕通过中心垂直于盘面的轴沿图示方向转动时,(A)铜盘上有感应电流产生,沿着铜盘转动的相反方向流动.(B)铜盘上有感应电流产生,沿着铜盘转动的方向流动.(C)铜盘上产生涡流.(D)铜盘上有感应电动势产生,铜盘边缘处电势最高.(E)铜盘上有感应电动势产生,铜盘中心处电势最高.[]8(本题3分)两个相距不太远的平面圆线圈,怎样可使其互感系数近似为零?设其中一线圈的轴线恰通过另一线圈的圆心.(A)两线圈的轴线互相平行放置.(B)两线圈并联.(C)两线圈的轴线互相垂直放置.(D)两线圈串联.[]二填空题(共24分)9(本题3分)一半径为a的无限长直载流导线,沿轴向均匀地流有电流I.若作一个半径为R=5a、高为l的柱形曲面,已知此柱形曲面的轴与载流导线的轴平行且相距3a(如图).则在圆柱侧面S上的积分________________.\n10(本题3分)载有电流I的导线由两根半无限长直导线和半径为R的、以xyz坐标系原点O为中心的3/4圆弧组成,圆弧在yOz平面内,两根半无限长直导线与x轴平行,电流流向如图所示.O点的磁感强度____________________________________.(用坐标轴正方向单位矢量表示)11(本题4分)如图,平行的无限长直载流导线A和B,电流强度均为I,垂直纸面向外,两根载流导线之间相距为a,则(1)中点(P点)的磁感强度_____________.(2)磁感强度沿图中环路L的线积分__________________________________.12(本题3分)如图所示,在真空中有一半径为a的3/4圆弧形的导线,其中通以稳恒电流I,导线置于均匀外磁场中,且与导线所在平面垂直.则该载流导线bc所受的磁力大小为_________________.13(本题4分)判断在下述情况下,线圈中有无感应电流,若有,在图中标明感应电流的方向.(1)两圆环形导体互相垂直地放置.两环的中心重合,且彼此绝缘,当B环中的电流发生变化时,在A环中_______________________.(2)无限长载流直导线处在导体圆环所在平面并通过环的中心,载流直导线与圆环互相绝缘,当圆环以直导线为轴匀速转动时,圆环中__________________.14(本题4分)半径为L的均匀导体圆盘绕通过中心O的垂直轴转动,角速度为w,盘面与均匀磁场垂直,如图.(1)图上Oa线段中动生电动势的方向为_________________.(2)填写下列电势差的值(设ca段长度为d):Ua-UO=__________________.Ua-Ub=__________________.Ua-Uc=__________________.15(本题分3)真空中两只长直螺线管1和2,长度相等,单层密绕匝数相同,直径之比d1/d2=1/4.当它们通以相同电流时,两螺线管贮存的磁能之比为W1/W2=___________.\n三计算题(共47分)16(本题5分)一根无限长导线弯成如图形状,设各线段都在同一平面内(纸面内),其中第二段是半径为R的四分之一圆弧,其余为直线.导线中通有电流I,求图中O点处的磁感强度.17(本题12分)两个无穷大平行平面上都有均匀分布的面电流,面电流密度分别为i1和i2,若i1和i2之间夹角为q,如图,求:(1)两面之间的磁感强度的值Bi.(2)两面之外空间的磁感强度的值Bo.(3)当,时以上结果如何?18(本题5分)如图所示,有两根平行放置的长直载流导线.它们的直径为a,反向流过相同大小的电流I,电流在导线内均匀分布.试在图示的坐标系中求出x轴上两导线之间区域内磁感强度的分布.19(本题5分)通有电流I的长直导线在一平面内被弯成如图形状,放于垂直进入纸面的均匀磁场中,求整个导线所受的安培力(R为已知).20(本题10分)如图所示,两条平行长直导线和一个矩形导线框共面.且导线框的一个边与长直导线平行,他到两长直导线的距离分别为r1、r2.已知两导线中电流都为,其中I0和w为常数,t为时间.导线框长为a宽为b,求导线框中的感应电动势.21(本题10分)载有电流的I长直导线附近,放一导体半圆环MeN与长直导线共面,且端点MN的连线与长直导线垂直.半圆环的半径为b,环心O与导线相距a.设半圆环以速度平行导线平移,求半圆环内感应电动势的大小和方向以及MN两端的电压UM-UN.四回答问题(共5分)22(本题5分)用简单例子说明:楞次定律是能量守恒的必然结果.换句话说,如果电磁感应的规律正好与楞次定律相反,则能量守恒定律便不成立.参考答案一选择题(共24分)DCBCCDDC二填空题(共24分)9(本题3分)\n03分10(本题3分)3分11(本题4分)02分2分12(本题3分)3分13(本题4分)无感应电流2分无感应电流2分14(本题4分)Oa段电动势方向由a指向O.1分1分01分1分15(本题3分)1∶163分参考解:三计算题(共47分)16(本题5分)解:将导线分成1、2、3、4四部份,各部分在O点产生的磁感强度设为B1、B2、B3、B4.根据叠加原理O点的磁感强度为:∵、均为0,故1分方向Ä1分\n方向Ä1分其中,∴方向Ä2分17(本题12分)解:当只有一块无穷大平面存在时,利用安培环路定理,可知板外的磁感强度值为4分现有两块无穷大平面,与夹角为q,因,,故和夹角也为q或p-q.(1)在两面之间和夹角为(p-q)故2分(2)在两面之外和的夹角为q,故2分(3)当,时,有02分2分18(本题5分)解:应用安培环路定理和磁场叠加原理可得磁场分布为,4分的方向垂直x轴及图面向里.1分19(本题5分)解:长直导线AC和BD受力大小相等,方向相反且在同一直线上,故合力为零.现计算半圆部分受力,取电流元,即2分由于对称性∴3分方向沿y轴正向20(本题10分)解:两个载同向电流的长直导线在如图坐标x处所产生的磁场为2分选顺时针方向为线框回路正方向,则\n3分2分∴e3分21(本题10分)解:动生电动势为计算简单,可引入一条辅助线MN,构成闭合回路MeNM,闭合回路总电动势2分负号表示的方向与x轴相反.3分方向N→M2分3分四回答问题(共5分)22(本题5分)答:例如在磁棒靠近线圈时,线圈中产生感应电流,按楞次定律,线圈电流方向应如图所示,这样线圈阻碍磁棒靠近,使磁棒的动能转化为线圈的磁场能和线圈中因有电流而生的热.2分如果与楞次定律相反,线圈中感应电流的磁场将吸引磁棒,使磁棒加速,动能增加.这增加的动能、磁场能和线圈中生的热都系无中生有,显然违反能量守恒定律.3分恒定磁场一、选择题1.(本题3分,答案:C)电流I由长直导线1沿半径方向经a点流入一电阻均匀的圆环,再由b点沿切向从圆环流出,经长直导线2返回电源(如图).已知直导线上的电流强度I,圆环的半径R,且a、b和圆心O在一条直线上,设直电流1、2及圆环电流分别在O点产生的磁感强度、及,则O点的磁感强度大小\n(A)B=0,因为B1=B2=B3=0.(B)B=0,因为,B3=0.(C)B≠0,因为虽然B1=B3=0,但B2≠0.(D)B≠0,因为虽然B1=B2=0,但B3≠0.(E)B≠0,因为虽然B2=B3=0,但B1≠0..2.(本题3分,答案:C)边长为l的正方形线圈,分别用图15.2所示两种方式通以电流I(其中ab、cd与正方形共面),在这两种情况下,线圈在其中心产生的磁感强度的大小分别为:I·B1l(1)cdbaII·B2l(2)(A)B1=0.B2=0.(B)B1=0.(C).B2=0.(D)..3.(本题3分,答案:A)如图,无限长载流导线与三角形载流线圈在同一平面内,若长直导线固定不动,则载流三角形线圈将(A)向着长直导线平移(B)离开长直导线平移(C)转动(D)不动4.(本题3分,答案:B;09A)两根载流导线相互正交放置,如图所示,沿y轴的正方向,沿z轴的负方向.若载流的导线不能动,载流的导线可以自由运动,则载流的导线开始运动的趋势是(A)沿x方向平动(B)绕x轴转动(C)绕y轴转动(D)无法判断二、填空题1.(本题3分)沿着图示的两条不共面而彼此垂直的无限长的直导线,通过电流强度和的电流.在距离两导线皆为处的A点处,磁感强度的大小.(答案:)2.(本题3分)真空中载有稳恒电流的细线圈,则通过包围该线圈的封闭曲面S的磁通量.若通过S面上某面元的元磁通,而线圈中电流增加为时,通过同一面元的元磁通,则.(答案:0,1/2)3.(本题3分)半径为0.5cm的无限长直圆柱形导体上,沿轴线方向均匀地流着I=3A\n的电流.作一个半径r=5cm、长l=5cm且与电流同轴的圆柱形闭合曲面S,则该曲面上的磁感强度沿曲面的积分________________________.(答案:0)4.(本题3分)在安培环路定理中,是指_________________________________;是指________________,它是由_________________决定的.[答案:环路L所包围的所有稳恒电流的代数和(1分);环路L上的磁感强度(1分);环路L内外全部电流所产生磁场的叠加(1分)]5.(本题3分)有一同轴电缆,其尺寸如图所示,它的内外两导体中的电流为I,且在横截面上均匀分布,但二者电流的流向正相反,则(1)在处磁感强度大小为;(2)在处磁感强度大小为.(答案:,0)6.(本题3分)一密绕的细长螺线管,每厘米长度上绕有10匝细导线,螺线管的横截面积为10cm2,当在螺线管中通入10A的电流时,它的横截面上的磁通量为BS=4π×10-10韦伯.(真空中磁导率μ0=4π×10-7T.m/A)7.(本题3分)如图,一根载流导线被弯成半径为R的1/4圆弧,放在磁感强度为B的均匀磁场中,则载流导线ab所受磁场的作用力的大小为____________,方向_________________.[答案:(2分)沿y轴正向(1分)]8.(本题4分,09B)A、B、C为三根平行共面的长直导线,导线间距d=10cm,它们通过的电流分别为IA=IB=5A,IC=10A,其中IC与IA、IB的方向相反,每根导线每厘米所受的力的大小=0=15×10-7N/cm2=-15×10-7N/cm2(μ0=4π×10-7N/A2)9.(本题3分)真空中两只长直螺线管1和2,长度相等,单层密绕匝数相等,直径之比d1/d2=1/4,当它们通以相同电流时,两螺线管储存的磁能之比W1/W2=1/16.三、计算题1.(本题5分)\n平面闭合回路由半径为R1及R2(R1>R2)的两个同心半圆弧和两个直导线段组成(如图).已知两个直导线段在两半圆弧中心O处的磁感强度为零,且闭合载流回路在O处产生的总的磁感强度B与半径为R2的半圆弧在O点产生的磁感强度B2的关系为B=2B2/3,求R1与R2的关系.解:由毕奥-萨伐尔定律可得,设半径为R1的载流半圆弧在O点产生的磁感强度为B1,则(1分)同理,(1分)∵∴故磁感强度1分∴2分2.(本题5分)如图,1、3为半无限长直载流导线,它们与半圆形载流导线2相连.导线1在平面内,导线2、3在平面内.试指出电流元在O点产生的的方向,并写出此载流导线在O点的总磁感强度(包括大小和方向).解:电流元在O点产生的方向为(-z方向)电流元在O点产生的方向为(-x方向)电流元在O点产生的方向为(-x方向)3分2分3.(本题10分)将通有电流的无限长导线折成如图形状,已知半圆环的半径为.求圆心O点的磁感强度O解:O处总磁感强度.,方向垂直向里1分而1分又1分因O在cd延长线上因此1分4.(本题10分)横截面为矩形的环形螺线管,芯圆环内外半径分别为R1和R2芯子材料的磁导率为μ\n,导线总匝数为N,绕得很密,若线圈通电流I,求处(1)芯子中的B值和芯子截面的磁通量(2)在r≤R1,r≥R2处的B值解:(1)螺绕环内的磁场具有轴对称性,故在环内作与环同轴的安培环路.有=2prB=m0SIi=m0NIB=m0NI/(2pr)取面积微元hdr平行与环中心轴,有dFm=|B×dS|=[m0NI/(2pr)]hdr=m0NIhdr/(2pr)Fm=(2)根据对称性分析和安培环路定律,可得在r≤R1,r≥R2处的B值为零。5.(本题10分)一无限长柱形铜导线(磁导率),半径为R,通有均匀分布的电流.今取一矩形平面S(长为1m,宽为2R),位置如右图中画斜线部分所示,求通过该矩形平面的磁通量.解:在圆柱体内部与导体中心轴线相距为r处的磁感强度的大小,由安培环路定律可得:3分因而,穿过导体内画斜线部分平面的磁通2分在圆形导体外,与导体中心轴相距为r处的磁感强度的大小为2分因而穿过导体外画斜线部分平面的磁通1分穿过整个矩形平面的磁通量.1分6.(本题10分)半径为R的半圆线圈ACD通有电流I2,置于电流为I1的无限长直线电流的磁场中,直线电流I1恰过半圆的直径,两导线相互绝缘.求半圆线圈受到长直线电流I1的磁力.解:长直导线在周围空间产生的磁场分布为取xOy坐标系如图,则在半圆线圈所在处各点产生的磁感强度大小为:,方向垂直纸面向里,2分\n式中q为场点至圆心的联线与y轴的夹角.半圆线圈上dl段线电流所受的力为:2分.根据对称性知:Fy=2分,∴半圆线圈受I1的磁力的大小为:,方向:垂直I1向右.4分