大学物理大题

大学物理大题

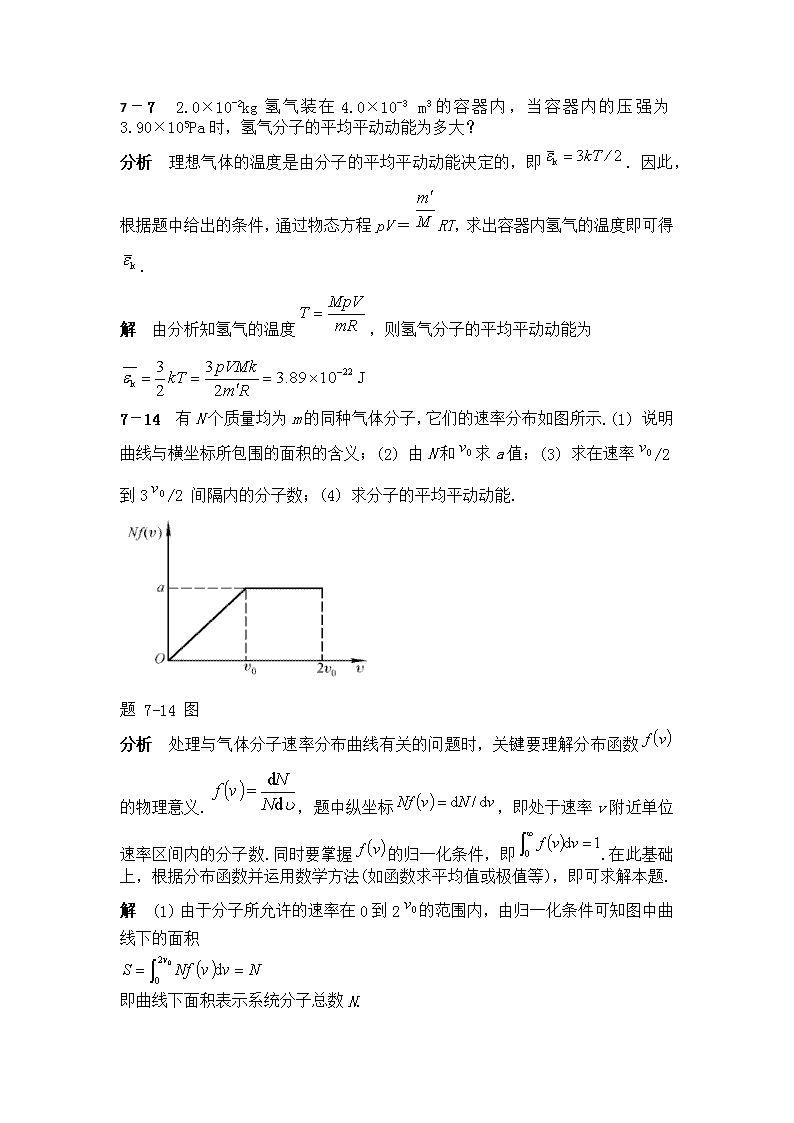
7－7　2.0×10-2kg氢气装在4.0×10-3m3的容器内，当容器内的压强为3.90×105Pa时，氢气分子的平均平动动能为多大？分析　理想气体的温度是由分子的平均平动动能决定的，即．因此，根据题中给出的条件，通过物态方程pV＝RT，求出容器内氢气的温度即可得．解　由分析知氢气的温度，则氢气分子的平均平动动能为7－14　有N个质量均为m的同种气体分子，它们的速率分布如图所示.(1)说明曲线与横坐标所包围的面积的含义；(2)由N和求a值；(3)求在速率/2到3/2间隔内的分子数；(4)求分子的平均平动动能.题7-14图分析　处理与气体分子速率分布曲线有关的问题时，关键要理解分布函数的物理意义.，题中纵坐标，即处于速率v附近单位速率区间内的分子数.同时要掌握的归一化条件，即.在此基础上，根据分布函数并运用数学方法(如函数求平均值或极值等)，即可求解本题.解　(1)由于分子所允许的速率在0到2的范围内，由归一化条件可知图中曲线下的面积即曲线下面积表示系统分子总数N.\n(2)从图中可知，在0到区间内，；而在0到2区间，.则利用归一化条件有a=2N/3v0(3)速率在/2到3/2间隔内的分子数为(4)分子速率平方的平均值按定义为故分子的平均平动动能为8－7　如图所示，1mol氦气，由状态沿直线变到状态，求这过程中内能的变化、对外作的功、吸收的热量.分析由题8-4分析可知功的数值就等于p-V图中过程曲线下所对应的面积，又对一定量的理想气体其内能，而氦气为单原子分子，自由度i=3，则1mol氦气内能的变化，其中温度的增量可由理想气体物态方程求出.求出了过程内能变化和做功值，则吸收的热量可根据热力学第一定律求出.解由分析可知，过程中对外作的功为内能的变化为吸收的热量\n题8-7图8－8　一定量的空气，吸收了1.71×103J的热量，并保持在1.0×105Pa下膨胀，体积从1.0×10－2m3增加到1.5×10－2m3，问空气对外作了多少功？它的内能改变了多少？分析　由于气体作等压膨胀，气体作功可直接由W＝p(V2－V1)求得.取该空气为系统，根据热力学第一定律Q＝ΔE＋W可确定它的内能变化.在计算过程中要注意热量、功、内能的正负取值.解　该空气等压膨胀，对外作功为W＝p(V2－V1)＝5.0×102J其内能的改变为ΔE＝Q－W＝1.21×103J8－10　一压强为1.0×105Pa,体积为1.0×10－3m3的氧气自0℃加热到100℃.问：(1)当压强不变时，需要多少热量?当体积不变时，需要多少热量?(2)在等压或等体过程中各作了多少功?分析　(1)由量热学知热量的计算公式为.按热力学第一定律，在等体过程中，；在等压过程中，(2)求过程的作功通常有两个途径.①利用公式；②利用热力学第一定律去求解.在本题中，热量Q已求出，而内能变化可由得到.从而可求得功W.解　根据题给初态条件得氧气的物质的量为氧气的摩尔定压热容，摩尔定容热容.(1)求Qp、QV等压过程氧气(系统)吸热\n等体过程氧气(系统)吸热(2)按分析中的两种方法求作功值①利用公式求解.在等压过程中，，则得而在等体过程中，因气体的体积不变，故作功为②利用热力学第一定律Q＝ΔE＋W求解.氧气的内能变化为　由于在(1)中已求出Qp与QV，则由热力学第一定律可得在等压过程、等体过程中所作的功分别为8－11　如图所示，系统从状态A沿ABC变化到状态C的过程中，外界有326J的热量传递给系统，同时系统对外作功126J.当系统从状态C沿另一曲线CA返回到状态A时，外界对系统作功为52J，则此过程中系统是吸热还是放热？传递热量是多少？题8-11图分析　已知系统从状态C到状态A，外界对系统作功为WCA，如果再能知道此过程中内能的变化ΔECA，则由热力学第一定律即可求得该过程中系统传递的热量QCA.由于理想气体的内能是状态(温度)的函数，利用题中给出的ABC过程吸热、作功的情况，由热力学第一定律即可求得由A至C过程中系统内能的变化ΔEAC，而ΔEAC＝－ΔECA，故可求得QCA.解　系统经ABC过程所吸收的热量及对外所作的功分别为QABC＝326J，　WABC＝126J则由热力学第一定律可得由A到C过程中系统内能的增量\nΔEAC＝QABC－WABC＝200J由此可得从C到A，系统内能的增量为ΔECA＝－200J从C到A，系统所吸收的热量为QCA＝ΔECA＋WCA＝－252J式中负号表示系统向外界放热252J.这里要说明的是由于CA是一未知过程，上述求出的放热是过程的总效果，而对其中每一微小过程来讲并不一定都是放热.8－12　如图所示，使1mol氧气(1)由A等温地变到B；(2)由A等体地变到C，再由C等压地变到B.试分别计算氧气所作的功和吸收的热量.题8-12图分析　从p－V图(也称示功图)上可以看出，氧气在AB与ACB两个过程中所作的功是不同的，其大小可通过求出.考虑到内能是状态的函数，其变化值与过程无关，所以这两个不同过程的内能变化是相同的，而且因初、末状态温度相同TA＝TB，故ΔE＝0，利用热力学第一定律Q＝W＋ΔE，可求出每一过程所吸收的热量.解　(1)沿AB作等温膨胀的过程中，系统作功由分析可知在等温过程中，氧气吸收的热量为QAB＝WAB＝2.77×103Ｊ　　(2)沿A到C再到B的过程中系统作功和吸热分别为WACB＝WAC＋WCB＝WCB＝(VB－VC)＝2.0×103ＪQACB＝WACB＝2.0×103Ｊ8－140.32kg的氧气作如图所示的ABCDA循环，V2＝2V1,T1＝300Ｋ，T2＝200Ｋ,求循环效率.\n题8-14图分析　该循环是正循环.循环效率可根据定义式η＝W/Q来求出，其中W表示一个循环过程系统作的净功，Q为循环过程系统吸收的总热量.解　根据分析，因AB、CD为等温过程，循环过程中系统作的净功为由于吸热过程仅在等温膨胀(对应于AB段)和等体升压(对应于DA段)中发生,而等温过程中ΔE＝0,则.等体升压过程中W＝0，则,所以，循环过程中系统吸热的总量为由此得到该循环的效率为14-8　在双缝干涉实验中，两缝间距为0.30mm，用单色光垂直照射双缝，在离缝1.20m的屏上测得中央明纹一侧第5条暗纹与另一侧第5条暗纹间的距离为22.78mm．问所用光的波长为多少，是什么颜色的光？分析与解　在双缝干涉中，屏上暗纹位置由决定，式中d′为双缝到屏的距离，d为双缝间距．所谓第5条暗纹是指对应k＝4的那一级暗纹．由于条纹对称，该暗纹到中央明纹中心的距离，那么由暗纹公式即可\n求得波长λ．此外，因双缝干涉是等间距的，故也可用条纹间距公式求入射光波长．应注意两个第5条暗纹之间所包含的相邻条纹间隔数为9（不是10，为什么？），故.解1　屏上暗纹的位置，把以及d、d′值代入，可得λ＝632.8nm，为红光．解2　屏上相邻暗纹（或明纹）间距，把，以及d、d′值代入，可得λ＝632.8nm．14-11　如图所示，将一折射率为1.58的云母片覆盖于杨氏双缝上的一条缝上，使得屏上原中央极大的所在点O改变为第五级明纹.假定=550nm，求：（1）条纹如何移动？（2）云母片的厚度t.题14-11图分析　(1)本题是干涉现象在工程测量中的一个具体应用，它可以用来测量透明介质薄片的微小厚度或折射率．在不加介质片之前，两相干光均在空气中传播，它们到达屏上任一点P的光程差由其几何路程差决定，对于点O，光程差Δ＝0，故点O处为中央明纹，其余条纹相对点O对称分布．而在插入介质片后，虽然两相干光在两介质薄片中的几何路程相同，但光程却不同，对于点O，Δ≠0，故点O不再是中央明纹，整个条纹发生平移．原来中央明纹将出现在两束光到达屏上光程差Δ=0的位置.(2)干涉条纹空间分布的变化完全取决于光程差的变化．因此，对于屏上某点P（明纹或暗纹位置），只要计算出插入介质片前后光程差的变化，即可知道其干涉条纹的变化情况．插入介质前的光程差Δ1＝r1－r2＝k1λ（对应k1级明纹），插入介质后的光程差Δ2＝（n－1）d＋r1－r2＝k1λ（对应k1级明纹）．光程差的变化量为Δ2－Δ1＝（n－1）d＝（k2－k1）λ式中（k2－k1）可以理解为移过点P的条纹数（本题为5）．因此，对于这类问题，求解光程差的变化量是解题的关键．解　由上述分析可知，两介质片插入前后，对于原中央明纹所在点O，有\n将有关数据代入可得14-12　白光垂直照射到空气中一厚度为380nm的肥皂膜上．设肥皂的折射率为1.32．试问该膜的正面呈现什么颜色？分析　这是薄膜干涉问题，求正面呈现的颜色就是在反射光中求因干涉增强光的波长（在可见光范围）．解　根据分析对反射光加强，有在可见光范围，k＝2时，（红光）k＝3时，（紫光）故正面呈红紫色．14-14　集成光学中的楔形薄膜耦合器原理如图所示．沉积在玻璃衬底上的是氧化钽（）薄膜，其楔形端从A到B厚度逐渐减小为零．为测定薄膜的厚度，用波长λ＝632.8nm的激光垂直照射，观察到薄膜楔形端共出现11条暗纹，且A处对应一条暗纹，试求氧化钽薄膜的厚度．（对632.8nm激光的折射率为2.21）题14-14图分析　置于玻璃上的薄膜AB段形成劈尖，求薄膜厚度就是求该劈尖在A点处的厚度．由于对激光的折射率大于玻璃，故从该劈尖上表面反射的光有半波损失，而下表面没有，因而两反射光光程差为Δ＝2ne＋λ/2．由反射光暗纹公式2nek＋λ/2＝（2k＋1）λ/2，k＝0，1，2，3，…，可以求厚度ek．又因为AB中共有11条暗纹（因半波损失B端也为暗纹），则k取10即得薄膜厚度．解　根据分析，有2nek＋＝（2k＋1）λ/2　（k＝0，1，2，3，…）\n取k＝10，得薄膜厚度e10＝＝1.4×10-6m．14-20　如图所示，狭缝的宽度b＝0.60mm，透镜焦距f＝0.40m，有一与狭缝平行的屏放置在透镜焦平面处．若以波长为600nm的单色平行光垂直照射狭缝，则在屏上离点O为x＝1.4mm处的点P看到的是衍射明条纹．试求：（1）点P条纹的级数；（2）从点P看来对该光波而言，狭缝的波阵面可作半波带的数目．分析　单缝衍射中的明纹条件为，在观察点P位置确定（即衍射角φ确定）以及波长λ确定后，条纹的级数k也就确定了.而狭缝处的波阵面对明条纹可以划分的半波带数目为（2k＋1）条．解　（1）设透镜到屏的距离为d，由于d＞＞b，对点P而言，有．根据分析中的条纹公式，有将b、d（d≈f）、x,λ的值代入，可得k＝３（2）由分析可知，半波带数目为7.14-24　一束平行光垂直入射到某个光栅上，该光束中包含有两种波长的光：λ1＝440nm和λ2＝660nm．实验发现，两种波长的谱线（不计中央明纹）第二次重合于衍射角φ＝60°的方向上，求此光栅的光栅常数．分析　根据光栅衍射方程，两种不同波长的谱线，除k＝0中央明纹外，同级明纹在屏上位置是不同的，如果重合，应是它们对应不同级次的明纹在相同衍射角方向上重合．故由dsinφ＝kλ1＝k′λ2可求解本题．解　由分析可知，得得\n上式表明第一次重合是λ1的第3级明纹与λ2的第2级明纹重合，第二次重合是λ1的第6级明纹与λ2的第4级明纹重合．此时，k＝6，k′＝4，φ＝60°，则光栅常数16－8　钨的逸出功是4.52eV，钡的逸出功是2.50eV，分别计算钨和钡的截止频率.哪一种金属可以用作可见光范围内的光电管阴极材料？分析　由光电效应方程可知，当入射光频率ν＝ν0(式中ν0＝W/h)时，电子刚能逸出金属表面，其初动能.因此ν0是能产生光电效应的入射光的最低频率(即截止频率)，它与材料的种类有关.由于可见光频率处在0.395×1015～0.75×1015Hz的狭小范围内，因此不是所有的材料都能作为可见光范围内的光电管材料的(指光电管中发射电子用的阴极材料).解　钨的截止频率　钡的截止频率　对照可见光的频率范围可知，钡的截止频率正好处于该范围内，而钨的截止频率大于可见光的最大频率，因而钡可以用于可见光范围内的光电管材料.16－9　钾的截止频率为4.62×1014Hz，今以波长为435.8nm的光照射，求钾放出的光电子的初速度.解　根据光电效应的爱因斯坦方程其中W＝hν0，　ν=c/λ可得电子的初速度由于逸出金属的电子的速度v＜＜c，故式中m取电子的静止质量.16－10　在康普顿效应中，入射光子的波长为3.0×10－3nm，反冲电子的速度为光速的60％，求散射光子的波长及散射角.分析　首先由康普顿效应中的能量守恒关系式，可求出散射光子的波长λ，式中m为反冲电子的运动质量，即m＝m0(1－v2/c2)－1/2.再根据康普顿散射公式，求出散射角θ，式中λC\n为康普顿波长(λC＝2.43×10－12m).解　根据分析有(1)m＝m0(1－（v2/c2）)－1/2(2)(3)由式(1)和式(2)可得散射光子的波长将λ值代入式(3)，得散射角