- 2022-08-16 发布 |
- 37.5 KB |
- 53页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
大学物理 刚体
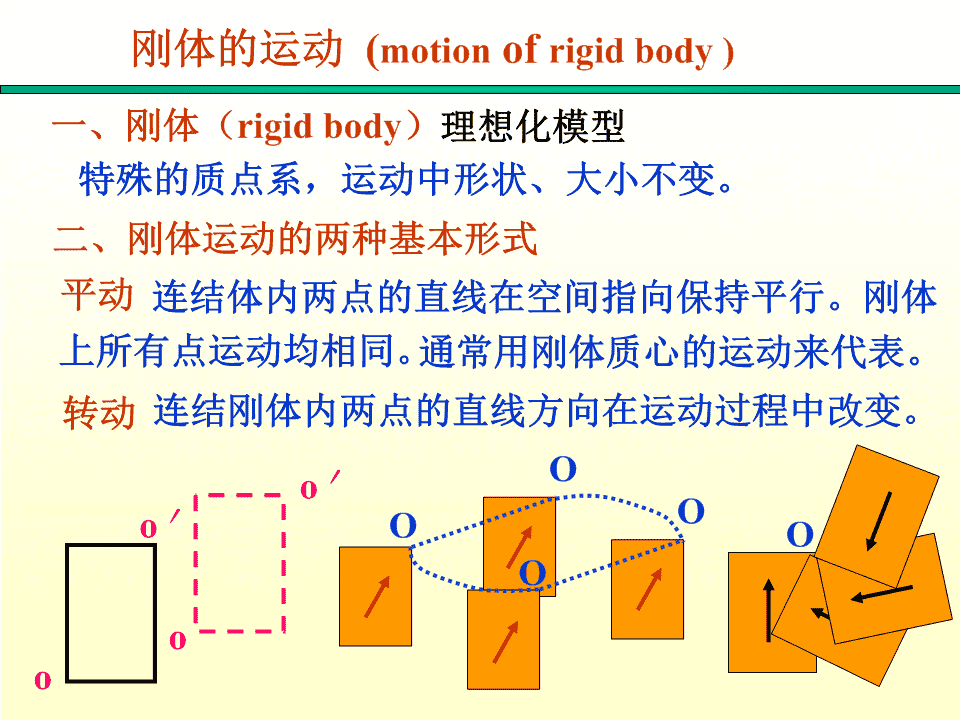
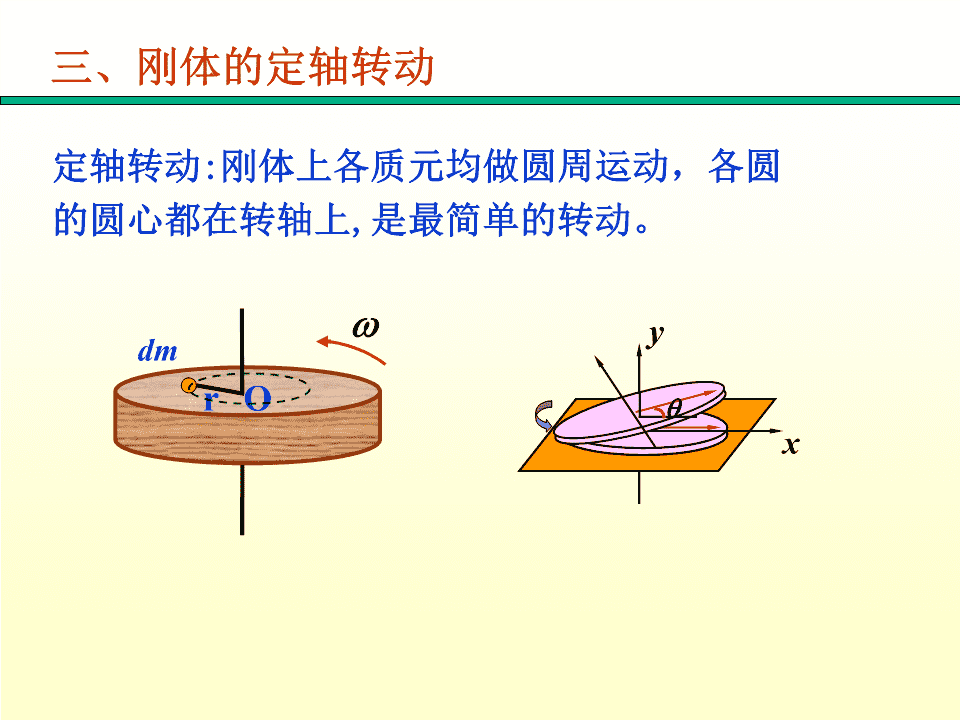
第三章:刚体的定轴转动(rotationofarigidbodyaboutafixedaxis)\n刚体的运动(motionofrigidbody)一、刚体(rigidbody)理想化模型特殊的质点系,运动中形状、大小不变。二、刚体运动的两种基本形式平动连结体内两点的直线在空间指向保持平行。刚体上所有点运动均相同。通常用刚体质心的运动来代表。转动连结刚体内两点的直线方向在运动过程中改变。Oo′Oo′OOOoo\n三、刚体的定轴转动定轴转动:刚体上各质元均做圆周运动,各圆的圆心都在转轴上,是最简单的转动。ydmrOx\n四、刚体的角量描述定轴转动时,刚体上任意点都绕同一轴作圆周运动。各质点的角量都相同。位置角vm11O角位移Δθ1x大小:dv2m2角dtO2x速度方向:右手四指转动方向,拇指为方向。2dd角加速度2dtdt\n线量与角量关系:zvrvvrrr)r//dvrPartθdtar2rn刚体O×匀加速定轴转动t0定轴12const.tt02222()00\n转动惯量的计算一、转动惯量刚体对某一转轴的转动惯量等于各质元质量与各质元到轴线垂直距离平方的乘积22Jmiri(分立)Jrdm(连续)m2222Jrdmrdvrdsrdlmmmm体积面积线J反映刚体转动惯性的大小dm(1)与刚体的质量有关。如铁盘与木盘rm(2)在质量相同的情况下,与质量的分布有关,如:圆盘与圆环。(3)与转轴的位置有关。\n二、几种典型刚体的转动惯量例1:均匀圆环对于中心垂直轴的转动惯量ddm(1)选取微元dmCRmmmdmdlRdd2R222m(2)求dJdJRdmRd22m22(3)求JJRdmR022JmR相当于质量为m的质点对轴的Jc\nrdldθ(2)绕沿直径轴的转动惯量θ22222dJrdmRcosdlRcosRd22mR32JRcosd02\n例2:求均匀薄圆盘对于中心垂直轴的转动惯量解:可视圆盘由许多小圆环组成。(1)选微元dmCRmmdmds2rdr2rdr2R(2)求dJdJ=r2dmrr(3)求J0Rm1222Jrdmr2rdrmRm0R22dr12JmR2\nydm例3圆球体,轴沿直径(y)12122RdJdmx(xdy)x22ox2dmdVxdyz222RxyR122222JdJ(Ry)dymRR25\n例4:求均匀细杆对中心轴及边缘轴的转动惯量m对质心轴(1)dmdxdxlx(2)dJx2dmx2dxACmxL022dx(3)JdJxdxLLcL22m212ml1212对边缘轴AJmlA13对质心轴Jml2lcl2131112Jxdxx32Alml03330可见,质量相同,形状相同,转轴不同,J不同。\n三.关于J的几条规律JCJ1.对同一轴J具有可叠加性OCdmmJ=JioRM2.平行轴定理平行2JJmdJ1MR2mR2co2其中:Jc:刚体对过质心轴的转动惯量J:刚体对平行于过质心轴的轴的转动惯量d:两平行轴间的距离由平行轴定律可见,在各平行的转轴中,通说明过质心的转轴对应的转动惯量最小。\n由前面例4中结果JJmd2ACmAC20m2L12LmmLLL122322又如求均匀薄圆盘对于通过其边缘一点O的平行轴的转动惯量:2mJJmdOC122COJmRmRoR232mR2\nO例5.图示一钟摆模型,由一根均匀细A杆和均匀薄圆板组成。细杆OA长为L,质量为m1,圆板C的半径为R,质量为Cm2。这一钟摆模型绕轴摆动,轴过杆端O垂直于板所在平面。试求这模型的转动惯量。解:应用平行轴定理总J=细杆的J1+圆板的J212122JmLmRm(RL)12232\nP书127,3-5\n刚体的定轴转动定律(lawofrotationofarigidbodyaboutafixedaxis)一、力矩是改变刚体转动状态的原因1.力在转动平面内MrFM=Fd=FrsinjFrjMd当M=0时,刚体匀速转动或静止\n2.力不在转动平面内FF1M=r×F=r×(F+F)12转动Fr2=r×F+r×F平面12r×F只能引起轴的1变形,对转动无贡献。在定轴转动问题中,所考虑的力矩是指力在转动平面内的分力对转轴的力矩。\n二﹑转动定律把刚体看成由N个质点组成的质点系对miFi—外力,刚体以外其他物体对mi的合力fi—内力,刚体内其它质点对mi的合力zω,α利用牛顿第二定律fFiFifimaiiirθFfmaiininiinmΔiFfmaititiit刚体Fin与fin对转轴的力矩为零Ffrmarititiiiti定轴ariti\nM=r×F2上式Fsinrfrsinmriiiiiiii对所有质点列出此式,并求和2Frisiniifrisiniimriiiii内力矩成对出现,且大小相等fisiniri0方向相反,作用在一条直线上22M外zFisinirimirimrii22刚体的转动惯量JzmirirdmJ反映刚体转动惯性的大小连续体\n刚体的定轴转动定律MJ外zz刚体所受的对于某固定转轴的合外力矩等于刚体对同一转轴的转动惯量与它所获得的角加速度的乘积。1.M是对z轴外力矩的代数和讨论外z力矩的正方向:与方向相同的力矩取正与方向相反的力矩取负2.定轴下可不写角标zMJ3.与牛顿第二定律比较M~FFmaJ~mMJ~a\n例:某飞轮直径d=50cm,绕中心垂直轴转动,转动惯量J=2.4千克·米2,转速n0=1000转/分,若制动时闸瓦对轮的压力为N=50千克力,闸瓦与轮间的滑动摩擦系数=0.4问:制动后飞轮转过多少圈停止?(1)求ffNddMf以向外为正2由转动定律MJM0.4509.80.25220.4弧度/秒J2.4\nt0(2)求圈数12tt022222202()0022n002602n030270弧度220.4270N43圈2\nz复习v刚体定轴转动的角量描述rP位置角角位移Δθθd角大小:速dt刚体r参度O×考方向:与转动方向成右方ω手螺旋向dω定轴角加速度ααdt线量与角量关系const.vrt01dv2ar0ttt2dt22ar202(0)n\n复习力矩是改变刚体转动状态的原因MrF2转动惯量JrdmmxACmCCRmR0mdx12JmR2JmRc212对边缘轴JAml312平行轴定理对质心轴Jcml212JJcmd\n质点(系)刚体复习drdvdtdt2dvdrddd2a2dtdtdtdtdt22mJrdmVFmaMJ\n转动定律应用举例MJ两类问题:第一类:由角量运动,求力矩。(微分法)第二类:由力矩及初始条件,求刚体运动。(积分法)特别注意:1.明确转动轴位置。2.选定转动的正方向,注意力矩、角速度、角加速度的正负。3.同一方程式中所有量都必须相对同一转轴。1.认刚体;2.定转轴,找运动;解题步骤:3.分析力和力矩;4.定转向,列方程。\n例1.己知:定滑轮为均匀圆盘,其上绕一细绳,绳一端固定在盘上,另一端挂重物m。绳与轮无相对滑动,绳不可伸长。轮半径R=0.2m,m=1kg,m下落时间t=3s,v0=0,h=1.5m。求:轮对O轴J=?解:轮与m为联结体,轮为定轴R转动、m为平动,但二者用绳联·系起来。m的速度大小与轮边定轴O绳v=0缘线速度大小相等。0mT'=-TNthamGTmg对轮:TRJ(1)对m:mgTma(2)\nTRJ(1)mgTma(2)a运动学关系:=(3)R1h=at2(4)22gt2联立解得:J(1)mR2h29.8322(1)10.21.14(kgm)21.5\n例2:如图,设滑块A,重物B及滑轮C的质量分别为MA,MB,MC。滑轮C是半径为r的均匀圆板。滑块A与桌面之间,滑轮与轴承之间均无摩擦,轻绳与滑轮之间无滑动。求:(1)滑块A的加速度a(2)滑块A与滑轮C之间绳的张力T1,(3)滑轮C与重物B之间绳的张力T2。NT′T21ACN′ABTB1MCgT2′MgAMgB解:T1T1T2T2对A:MAgN对C:Mcg及N都通过质心,力矩为零。\n选正方向列方程ATMa1ACTrTrJAC21cBMgTMaB2BB12a其中JcMcr2r解方程得MBgMAMBgaT111MAMBMCMAMBMC221M0时aMBgMAMCMBgCMM2ABT21MBMAgMAMBMCT1T22MMAB\n例.如图,两圆轮的半径分别为R1和R2,质量分别为M1和M2,皆可视为均匀圆柱体且同轴固结在一起,二盘边缘绕有细绳,绳子下端挂两个质量分别为m1和m2的物体,求在重力作用下,m2下落时轮的角加速度。解:m1:T1m1gm1a1m:mgTma22222TT12对整个轮,由转动定律1212Τ2R2Τ1R1(Μ1R1Μ2R2)αm1m222aa12由运动学关系α因为连体RR12mRmRg2211联立解得M12M22m1R1m2R222\n例.如图,两圆轮的半径分别为R1和R2,质量分别为M1和M2,皆可视为均匀圆柱体且同轴固结在一起,二盘边缘绕有细绳,绳子下端挂两个质量分别为m1和m2的物体,求在重力作用下,m2下落时轮的角加速度。另解:把两圆盘和两重物看作一个整体,T1T2这样绳子的拉力就是内力,只考虑重力这一外力矩m1mMmgRmgRJ211220JJJJJ01234mRmRg2211联立解得M12M22m1R1m2R222\nT1已知:A轮:R1,m1,受恒力矩M.2B轮:R,m122MAB轮与皮带间无滑动。R求:两轮的角加速度。1R2T2解:A、B正确解:MJ11J22A:MT1R1T2R1J11 (1)R11R22切向加速度B:T2R2T1R2J22 (2)112RR (3)JmR11221112212JmR (4)1111221JmR222212JmR (5)22222关键点:两轮的转轴不同(1)(2)\n定轴转动中的功能关系一.力矩的功dAFdrFdrcosFFrdsinMddAdAMdθrωθzM应理解为合外力矩·轴x内力矩的功AMd0内内\n二.定轴转动动能定理dAMdMdtd转动定律MJJdtddAJdtJddt21212A12JdJ2J112212刚体转动动能就刚体的转动动能:EkJ2是组成刚体的各1212可以证明:Jmivi质点平动动能之22和,它们是动能定轴转动动能定理:A外EK2EK1的不同表达形式合外力矩对定轴转动刚体所作的功等于刚体转动动能的增量\n三、刚体的重力势能各质元重力势能的总和,就是刚体的重力势能。EpmighigmihiiiΔmiC×mhiiimgmghchhmciEmghE=0pcp刚体的重力势能等于其质量集中在质心时所具有的重力势能\n四、定轴转动的功能原理质点系功能原理对刚体仍成立:AAEk2Ep2Ek1Ep1外非保守内力若体系是一个包含刚体、质点、弹簧等复杂系统时1212EkmvJ.....22Ep应包括系统中所有物体的势能五、机械能守恒定律对于包括刚体在内的体系,若只有保守内力作功AA0外非保守内力则系统机械能守恒EEConst.kp\n例:已知圆盘半径为R,质量为M,在垂直平面内可绕过中心水平轴转动,将跨在圆盘上的轻绳分别联接倔强系数为k的弹簧和质量为m的物体,设轮轴光滑,绳不伸长,绳与轮间无相对滑动,今用手托住m使弹簧保持原长,然后静止释放。求(1)m下落h距离时的速度。(2)弹簧的最大伸长量。解:取m+M+绳+弹簧+地球为一系统外力:轴承支承力和地面对弹M簧的支承力功为零。R内力:重力,弹性力为保守力,m绳与轮间无相对滑动,摩擦力功kh为零。\n系统机械能守恒1212121mghmv1Jkh下落h处势能为零222v112JMRMR2R24mgh2khmv12mMkh弹簧的最大伸长量?即:v01122mg2mgYkYYY为弹簧的最大伸长量2kmgv的最大值?Yk\n[例题]已知均质棒m,l,半径忽略的小球m组成图示系统,求图棒中心aatnI态I态II态,E守恒EE0图(2)60°JJJ1214l(ml2)2mglsin600mgsin600232mgII态93gmg8ll00MrFmgsin30mglsin302l9g3amglt23249gl93gM/Ja2()n16l216\n对定轴的角动量守恒(conservationofangularmomentumaboutafixedaxis)dL一、质点系角动量定律Mdt分量式:dLxdLydLzMxMyMzdtdtdt质点系对某轴的角动量随时间的变化率等于质点系中各质点所受外力对同一轴的力矩的代数和。t2对于有限时间MdtLLt211质点系角动量守恒定律M0L1L2或Mz0Lz1Lz2\n二、刚体的角动量定律刚体可以看成是由n个质点组成当其绕固定轴转动时,则其上各点都绕该轴作圆周运动zmm1m2...mi...mnrimir1r2rirn2对于mLrmvmriiziiiii22LLmrmrziziiiiiii2刚体对Z轴的转动惯量Jmirii刚体对于z轴的角动量LzJ\ndLz刚体定轴转动的角动量定理:Mzdtt2L2MdtdLLLJJzz212211t1L1刚体对某轴的冲量矩等于该段时间内刚体对同一轴角动量的增量三、角动量守恒定律若M0则L1L2或Mz0Lz1Lz2J11J22若所研究的系统中既包含刚体又包含质点、物体等,则M、L应理解为所有物体所受力矩和所有物体的角动量\n以下过程中那些物理量守恒?讨论'子细o子o圆o弹绳弹锥击质击摆T入量入沙不杆moR袋计vpvv以子弹和沙袋为系统以子弹和杆为系统圆锥摆系统动量守恒;动量不守恒;动量不守恒;O点角动量守恒;O点角动量守恒;O点角动量守恒;碰撞过程机械能不守恒。碰撞过程机械能不守恒。O’点角动量不守恒;碰撞后机械能守恒。碰撞后机械能守恒。机械能守恒。\n质点(系)刚体复习ddrvdtdt22dvdrddda22dtdtdtdtdt2mJrdmV\n质点(系)定轴转动刚体FmaMJpmvpmviiiLrpLJdpd(mv)dLd(J)FMdtdtdtdt动量守恒角动量守恒合外力为零,动量守恒合外力矩为零,角动量守恒\n例:质量为M,半径为R的水平放置的均匀圆盘,以角速度1绕垂直于圆盘并通过盘心的光滑轴,在水平面内转动时,有一质量为m的小物块以速度v垂直落在圆盘的边沿上,并粘在盘上,求:(1)小物块粘在盘上后,盘的角速度2=?(2)小物块在碰撞过程中受到的冲量I的方向及大小。m解:以m,M为一个系统,其沿轴向v合外力矩为零,轴向角动量守恒M2(1)JJmR2R盘1盘问:小球m的重力力矩方向?碰前m沿轴的角动量为零,但其动量不为零。12MRJ盘2M22111JmR122M2m盘MRmR2\n(2)求I应用动量定理IP2P1mv2mv1碰撞前后m动量方向不同,分方向讨论。平行于轴I0mvmv方向向上平行垂直于轴ImR0mR方向沿切线垂直2222II平行I垂直mvmRmvvtan(v和R所表示的速度不同)mRRmv角动量守恒时,动量不一定守恒。MR\n水平圆盘(m、R),盘边缘A处、距盘中心R/2的B处各站有一人,质量均为m/2。初始盘以0绕中心轴o转动,现A处的人相对盘以v顺圆盘转向作圆周运动,B处的人相对圆盘以2v逆圆盘转向运动,求此时圆盘。解:ω2vM外0L0常数vBJAJBJ0JJAAJBBAv1JmR2AR22vm2BRJAR22mR2J()B220\n[例]若对接前两轮的角速度分别为ω、ω12求:1.对接后共同的角速度、ωJ1J22.对接过程中的机械能损失解:由角动量守恒得:ωω12J1ω1J2ω2=(J1+J2)ωJ1ω1J2ω2ω=J1+J2ωΔEk=1(J+J)ω2(1Jω2+1Jω2)2122112222J1J2(ω1+ω2)摩擦力矩作负功,=<0有机械能损失。(J1+J2)\n例:一细杆质量为m,长为l,其一端可绕o轴在竖直平面内转动。开始时杆从水平位置静止释放,当杆摆到竖直位置时,杆下端恰好与墙上的小钉子碰撞,碰后杆能弹至与竖直方向成600角的位置,求:碰撞时钉子受到的冲量多大?o解:MdtJJ600MdtlFdtlFdtlIlIJ(J)J()(+)J()I (1)l\n碰撞前机械能守恒o600碰撞后机械能守恒l11223g碰前:mg(ml)(+)223ll011223g碰后:mg(1-cos60)(ml)2232lJ()13g3gIml()l3l2l\n作业:空心圆环绕AC轴自由转动,转动惯量J,环半径0R,初始角速度0,质量为m的小球静止于环内A点,由于微小干扰,小球向下滑到B点,环的角速度与小球相对于环的速度各为多大?(环内壁光滑)0解:小球、圆环对AC轴角动量守恒2J(JmR)①000BBAB小球、圆环、地球、系统机械能守恒121212JmgRJmv②000Bm地C222v环地vvvm地m环环地22222vvvvvR③m环vm地m环环地2m环Bm地由①②③vm环查看更多