计量经济学计算机作业

计量经济学计算机作业

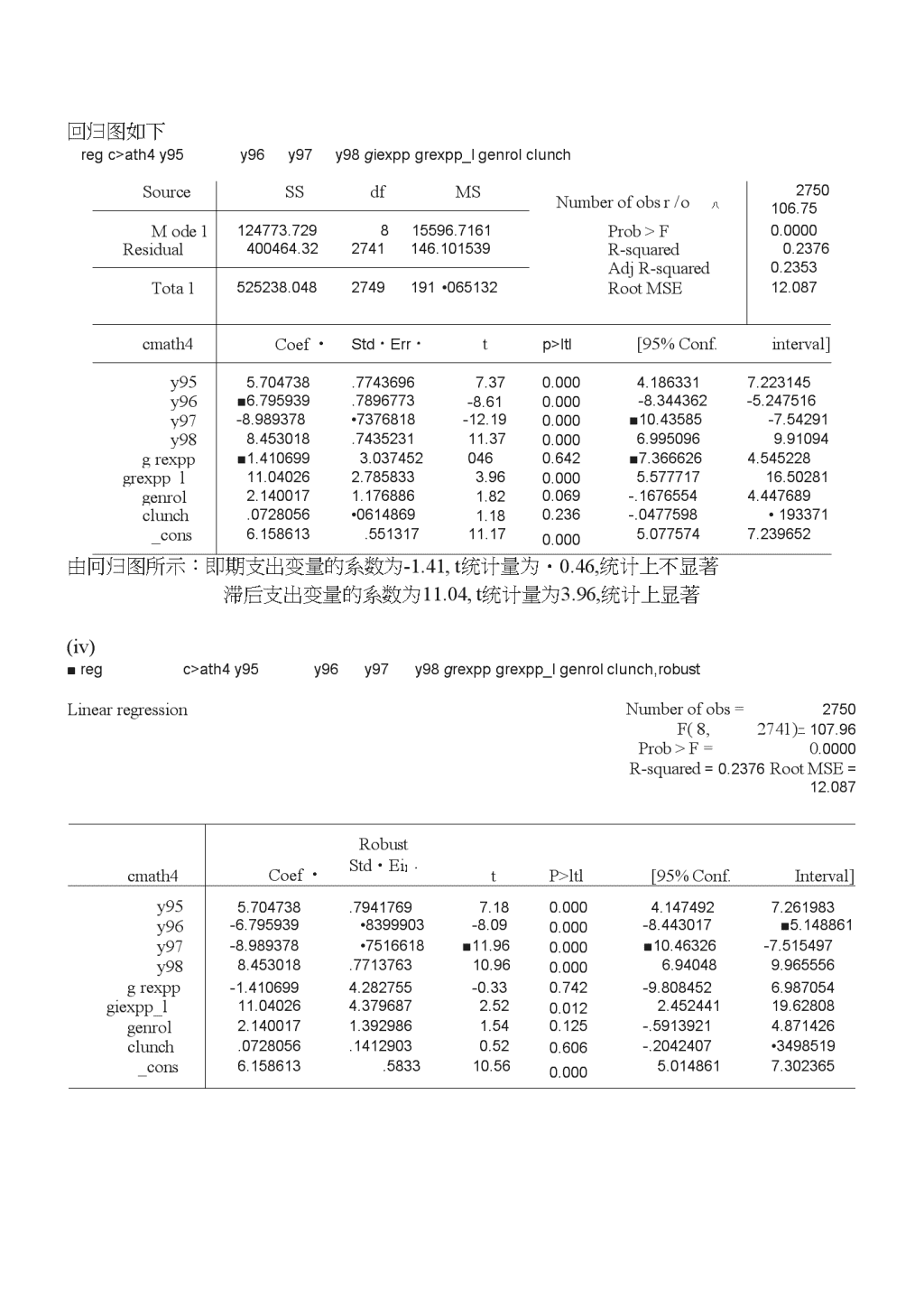
数量经济学付欢计量经济学计算机作业C13.ll(i)在其他自变量不变的情况下：根据:log(Xi)-log(X0)^(X1-X0)/Xo=AX/X()Amath4it=plAlog(rexppit)=(pl/100)*[100*Alog(rexppit)]«(pl/100)*(%Arexppit).因此if%Arexppit=10,thenAmath4it=(卩1/100)*(10)=01/10。所以，平均每个学生的真实支出提高10%,则math4it约改变01/10个百分点。(ii)用一阶差分估计第一部分中的模型(包括1994-1998年度虚拟变量)y94y95y96y97y98grexppgenrolclunchSourceSSdfMSMode1122398.669815299.8336Residual466100.0283291141.628693Total588498.6973299178.386995regc>ath4Numberofobs3300F(8,3291)108.03Prob>F0.0000R-squared0.2080AdjR-squared0.2061RootMSE11.901cmath4Coef・Std・Err・tp>ltl[95%Conf.Interval]y94.5210521.72837710.720.474-.90706611.94917y956.812446■77866368.750.0005.2357328.339161y96-5.23489.7271019-7.200.000■6.660508-3.809272y97-8.488463.7222014-11.750.000■9.9044727.55765-7.072453y988.967841■719233512.470.00010.37803grexpp-3.4472682.760079-1.250.212-8.8589131.964377genro1■63453351.0286030.620.537-1.3822332.6513clunch.025074.05547340.450.651・.083692•1338399_cons5.954963.518234711.490.0004.9388686.971058Amath4=5.95+.52y94+6.81y95-5.23y96-&49y97+8.97y98(0.52)(0.73)(0.78)(0.73)(0.72)(0.72)一3.45Alog(rexpp)+0.635Alog(enroll)+0.025Alunch(2.76)(1.029)(0.055)当rexpp增加10%,math4降低0.35%(3.45/10«0.35)(iii)在模型中添加支出变量的一阶滞后，并利用一阶差分估计得Amath4=6.16+5.70y95-6.80y96-&99y97+8.45y98(0.55)(0.77)(0.79)(0.74)(0.74)一1.41Alog(rexpp)+11.04Alog(rexpp-1)+2.14Alog(enroll)(3.04)(2.79)(1.18)+0.073Alunch(0.061)n=2,750,R2=0.238.\n回归图如下regc>ath4y95y96y97y98giexppgrexpp_lgenrolclunchSourceSSdfMSNumberofobsr/o八2750106.75Mode1124773.729815596.7161Prob>F0.0000Residual400464.322741146.101539R-squared0.2376AdjR-squared0.2353Tota1525238.0482749191•065132RootMSE12.087cmath4Coef・Std・Err・tp>ltl[95%Conf.interval]y955.704738.77436967.370.0004.1863317.223145y96■6.795939.7896773-8.610.000-8.344362-5.247516y97-8.989378•7376818-12.190.000■10.43585-7.54291y988.453018.743523111.370.0006.9950969.91094grexpp■1.4106993.0374520460.642■7.3666264.545228grexpp_l11.040262.7858333.960.0005.57771716.50281genrol2.1400171.1768861.820.069-.16765544.447689clunch.0728056•06148691.180.236-.0477598•193371_cons6.158613.55131711.170.0005.0775747.239652由冋归图所示：即期支出变量的系数为-1.41,t统计量为・0.46,统计上不显著滞后支出变量的系数为11.04,t统计量为3.96,统计上显著(iv)■regc>ath4y95y96y97y98grexppgrexpp_lgenrolclunch,robustLinearregressionNumberofobs=2750F(8,2741)二107.96Prob>F=0.0000R-squared=0.2376RootMSE=12.087cmath4Coef・RobustStd・Ei】・tP>ltl[95%Conf.Interval]y955.704738.79417697.180.0004.1474927.261983y96-6.795939•8399903-8.090.000-8.443017■5.148861y97-8.989378•7516618■11.960.000■10.46326-7.515497y988.453018.771376310.960.0006.940489.965556grexpp-1.4106994.282755-0.330.742-9.8084526.987054giexpp_l11.040264.3796872.520.0122.45244119.62808genrol2.1400171.3929861.540.125-.59139214.871426clunch.0728056.14129030.520.606-.2042407•3498519_cons6.158613.583310.560.0005.0148617.302365\n比较：0现(呦初的异方差稳健标准误为4.28,从而降低了Alog(rexpp)的统计显著性/\陽5(的异方差稳健标准误为4.38,其t统计量降低为2.52o在1%的显著性水平双侧检验下Alog(rexpp-1)仍然是统计显著的。(t统计量大于1.96)(V)clunch,robustxtregc>ath4y95y96y97y98gexppgexpp_lgenrollandom-effectsGLSregress1onroupvariable:distidHumberofobsNumberofgroups2750550>sq:withinbetweenoveral1tandomeffects：orr(u_i,X)0.24650.00540.2376Obspergroup:mm=avg=max=u_i~Gaussian二0(assumed)tfaldchi2(8)Prob>chi2762.120.0000(Std.Err.adjustedfor550clustersindistid)cmath4Coef.RobustStd・Err・zP>lzl[95%Conf.Interva1]y955.755012.90977856.330.0003.9718797.538145y96-6.773436•8658133-7.820.000-8.470399-5.076473y97■8.988665.7754606-11.590.000-10.50854-7.46879y988.514353.803080410.600.0006.94034410.08836gexpp-1.4107084.944105-0.290.775-11.100988.279559gexpp_l11.040265.1315022」50.031.982702321.09782genrol2.1400191.645121.300.193-1.0843575.364396clunch.0728056•16545640.440.660「251483•3970942_cons5.868631.77859637.540.0004.342617.394652sigma_usigma_erho013.1877390(ffactionofvarianceduetou_i)异方差序列相关稳健标准误为4.94,Alog(rexpp)的t统计量降低了。0血仏如)的标准误为5.13,Alog(rexpp-1)的t统计量为2.15.双侧检验的p值为0.032(vi)使用1995,1996,1997,1998年进行混合的OLS可得°二-0.423这表明差分误差有很强的负序列札I关(vii)基于充分稳健的联合检验，如下图\n"testgonro1cluneliC1)C2)genxol=Oclunch.=Ochi2(2)=Probachi2=1.860.3944所以模型中没有必要包含学生注册的人数和午餐项目变量C14.10(i)根据回归可知利用混合OLS估计的P1=0.36,当Aconcen=0.10,则Alfare=0.36*0.10=0.036.airfare增加3.6%>・reglfareconcenidistldistsqSourceSSdfMSHumberofobsF(3,4592)Prob>FR・squaredAdjR-squaredRootMSE45961015.850.00000.39890.3985.33845ModelResidua1349.089591526.00478234592116.363197・11454808Tota1875.0943744595.190444913lfareCoef・StdLErr・tP>ltl[95%Conf.interval]concenIdistldistsq_cons・3526892-.899166■10274636.249577.0302101•1290132■0097816.422965611.67-6.9710.5014.780.0000.0000.0000.000・2934628-1.152094・08356975.420361.4119157-.6462382.12192287.078793(ii)Bl的95%的置信区间为[0309,0.419]只有当复合误差序列无关，得出的标准误才是有效的，所以有点不太可能，充分稳健下的95%的置信区间为[0.245,0.475],条件为允许存在序列相关和异方差，所以充分稳健下的置信区间比一般的置信区间要大。忽略序列相关会导致参数估计产生不确定性.(iii).斜率变为正斜率的log(fare)的值为0.902/[2*0.103]~4.38。dist的值为exp(4.38)=80,该值表示的是fare对dist的正弹性系数。(iv)B1的RE估计值为0.209,表示fare与concern之间正相关。因为t=7.88估计值统计上显著\nRandom-effectsGLSregressionGroupvariable:idwithin=0.1270between=0.4018overal1=0.3876Randomeffects~Gaussiancorr(u_i,X)=0(assumed)Humberofobs二Numberofgroups=45961149Obspergroup:mm=4avg=4.0max=4Waldchi2(5)=1270.63Prob>chi2二0.0000lfarezP>lzI[95%Conf.Interval189ot99osyy1dcons•024341.00446445.450.000•0155911•033091•0350861.00446447.860.000■0263361.043836■0959191.004464421.490.000•0871691•1046691-.783627.2501516-3.130.002・1.273915「2933389.0897726•0188994.750.000.0527313•12681396.239633•82252837.590.0004.6275087.851759sigma_usigma,rho•32471182.10700501.90204224(ffactionofvarianceduetou_i)(i)FE估计值为0.169,RE的入估计值为09我们可以预计RE估计值与FE估计值非常相似。■xtregIfarey98y99yOOconcenldistldistsq,fenote:ldistomittedbecauseofcollinearitynote:ldistsqomittedbecauseofcolIinearityFtestthatalIui=0:F(1148,3443)=36.90Prob>F=0.0000Fixed-effects(within)regressionGroupvariable:idNumberofobs=Numberofgroups=45961149R-sq:within=0.1352Obspergroup:min=4between=0.0576avg=4.0overal1=0.0083max=4F(4,3443)=134.61corr(u_i,Xb)=-0.2033Prob>F=0.0000\nIfareCoef.Std-Err.tP>|t|[95%Conf.Interval]y98.0228328.00445155.130.000.0141048.0315607y99・0363819.00444958.180.000.0276579.0451058yOO.0977717.004455521.940.000.089036■1065073concen•168859.02941015.740.000.1111959.226522ldist(omitted)ldistsq(omitted)_cons4.953331.0182869270.870.0004.9174764.989185sigma_usigma_erho.43389176.10651186.94316439(fractionofvarianceduetou_i)\n(i)在一个航班线上的两个机场附近的城市影响航行的因素为人口，教育水平，雇主类型等。高速路及铁路的便利情况及周围的地理环境，可以考虑为固定不变的。这些因素和concern相关。SourceSSdfMSModel316.571003563.3142007Residual1442.441839269・155620005Total1759.012839274.189671429C15.8(i)■regpirap401kincincsqageagesq(ii)考虑到无法观测效应，我们可以使用固定效应模型得出估计值为正，且统计上显著。用FE估计得到的估计值为0.169concern与时间常量正相关Numberofobs=9275F(5,9269)=406.85Prob>F=0.0000R-squared=0.1800AdjR-squared=0.1795RootMSE二.39449piraCoef•Std・En・tP>ltl[95%Conf.Interval]p401k・0536598.00957135.610.000.0348978・0724217inc•0086788.00051116.980.000.0076771.0096806incsq-.00002284.03—065650.000-.0000307-.0000149age-.0015936.0033302-0.480.632-.0081216■0049343agesq.0001173.00003823.070.002.0000424.0001922_cons-.1977236•0686446-2.880.004-.332282-.0631651OLS估计方程:n=9,275,R2=0.180Pira=-0.198+0.054p401k+0.0087inc一0.000023inc2一0.0016age+0.00012age2(0.069)(0.010)(0.0005)(0.000004)(0.0033)(0.00004)p401k的系数表示保持收入和年龄不变的情况下，参加401(K)计划与拥有一个个人退休金账户的比没有参加401(K)计划与拥有一个个人退休金账户的概率多0.054o(ii)在上题的冋归方程中，保持收入和年龄不变下，在给定的收入和年龄等级中，该方程并不能解释不同的人有不同的储蓄计划。而是解释了储蓄的人会参加401(k)计划和(IRA)计划.在保持其他条件不变的情况下，如果无法控制个人的储蓄计划，用普通的OLS估计无法得到我们想要的结果(iii)欲使e401k成为p401k的有效IV,应该满足两个条件:e401k对p401k有偏效应和e401k0与u无法观测的储蓄计划不相关.如果雇主会提供401(k)退休计划的，工人会储蓄。则u与e401(k)相关。\n0.0011inc一0.0000018(ii)p401(k)的约简型方程P401k=0.059+0.689e401k+inc2一0.0047age+0.000052age2(0.046)(0.008)(0.0003)(0.0000027)(0.0022)(0.000026)n=9,275,R2=.596■regp401kincLinearregressionincsqageagesqe401k,robustlumberofobs=9275F(5,9269)=1915.11Prob>F=0.0000R-squared=0.5963RootMSE=.28418p401kCoef.RobustStd・Err・tP>ltl[95%Conf.Interval]me・0011117.00034340.001.0004384.0017849incsq1.84—062.67—060.491・3.40e-067.08e-06age-.0047205.0022433.1U0.035-.0091179-.0003231agesq.000052・00002570.0431.64—06.0001024e401k•6888454・007990386.210.000•6731827.7045082_cons.0591493.04617491.280.200-.0313637.1496623e401k的系数表示，在保持收入与年龄不变的情况下，有资格参与一项401(k)计划的人参加401(k)的计划会多0.69,明显的是，e401k符合成为p401k工具变量的两个要求之(iii)用e401k作为p401k的工具变量來估计Pira=-0.207+0.021p401k+0.0090inc一0.000024inc2-0.0011age+0.00011age2(0.065)(0.013)(0.0005)(0.000004)(0.0032)(0.00004)n=9,275,R2=0.180regpirayhatincageincsqagesq9robust.inearregressionNumberofobs=9275F(5,9269)=411.13Prob>F=0.0000R-squared=0.1774RootMSE=•3951piracoef.RobustStd.Err.tp>ltl[95%Conf.interval]yhat•inc•0207012.01324561.560.118-.0052631•0466654•0089982.00049161&300.000.0080345.009962age-.0011466.0032527-0.350.7240.000-.0075227•0052294incsq-.00002413.89e-06-6.21-.0000318-.0000165agesq■0001121.00003842.92O.OO4.0000368.0001873_cons-.2073136•0654498-3.170.002-.3356097-.0790176\nIV估计出来的Pp401k0.021低于OLS估计值0.054的一半。相应的t统计量值为1.56.约简型屮"mm就是给定无法观测的储蓄计划下的估计值。但是我们仍然无法估计参加401(K)计划与拥有个人退休金账户之间的替换关系。C17.ll•dropifhours=0"2348observationsdeleted).sumhoursvariableobsMeanStd.Dev.MinMaxhours328635.52921:LO・90291120(i)参加劳动的妇女的比率为3286/5634(总数)=0.583・(H)sourceSSdfMSModel185.581829537.1163657Residual720.0075723280.219514504Total905.5894013285.275674095•reglwageeducexperexpersqblackhispanicNumberofobs3286F(5,3280)169.08Prob>F0.0000R-squared0.2049AdjR-squared0.2037ROOtM5E.46852lwagecoef.std.Err.tp>ltl[95%Conf.interval]educ・0991502・003589827.620.000・0921118・1061887exper.0198554.00328566.040.000.0134133•0262974expersq-.0003489.000077-4.530.000-.0004999-.0001979black-.0295532.0343431-0.860.390-•0968892•0377828hispardc.0136158.03635650.370.708-•0576679•0848996_cons•648842•059965910.820.000•5312675•7664164•testblackhispanic(1)black=0(2)hispanic=0F(2,3280)=0.46Prob>F=0.6324只利用工作女性的数据用OLS估计工资方程:\nlog(wage)=0.649十0.099educ+0.020exper一0.00035exper2-0.030black+0.014hispanic(0.060)(0.004)(0.003)(0.00008)(0.034)(0.036)n=3,286,R2=0.205平均來说与非黑种人及非西班牙人群组相比，黑种多赚3%,西班牙人多赚1.3%,联合F检验的p值为0.63.所以当控制教育及经验水平下，不同种族之间工资差别不明显。(iii)nwifeinc的系数为-0.0091,t统计量为J3.47,kidlt6的系数为・0.5且t统计量为-11.05我们期待这两个系数为负。如果一个女人的丈夫赚更多的，她不太可能工作。有一个年轻的孩子在家庭中也降低了概率的女人。每个变量是非常显着。■probitinlfeducexperexpersqblackhispanicnwifeinckidlt6Iteration0:loglikelihood=-3826.743Iteration1:loglikelihood=-3537.4368Iteration2:loglikelihood=-3537.2544Iteration3:log1ikelihood=-3537.2544ProbitregressionNumberofobs=5634LRchi2(7)=578.98Prob>chi2=0.0000Loglikelihood=-3537.2544PseudoR2=0.0756inlfCoef.Std.Err.zP>|z|[95%Conf.Interval]educ・0964837・007785412.390.000・0812246.1117428exper.0077141.00723851.070.287-.0064732.0219014expersq-.0006143.0001577-3.900.000-.0009234-.0003052black.0167548.07558960.220.825-.1313981■1649077hispanic-.1219554.0704695-1.730.084-.260073.0161623nwifeinc-.0091239.0006775-13.470.000-.0104518-.007796kidlt6-.500167.0452776-11.050.000-.5889096-.4114245_cons-.4393231.1338545-3.280.001-.7016732-.176973(iv)我们需要至少一个影响参加劳动的变量，这个变量并不会直接影响工资的多少。所以,我们必须假定，控制教育、经验和种族差异变量下，其他收入和有一个孩子的情况并不不影响工资。如果雇主歧视有小孩或是丈夫有工作的妇女。这些假定就不会成立。此外，如果有一个孩子会降低劳动力，也就是说她必须花时间去照顾生病的孩子。这样，我们就不能从工资方程屮遗漏掉kidlt6o(i)每个观测的逆米尔斯比为1.77,相应的双侧p值为0.77.在3286个观测中，它并不是特别小的，久的检验并没有提供有力的证据对零假设没有选择偏差。\n(i)把逆米尔斯比加到工资方程中去，斜率系数并没有改变多少。例如education的系数从0.099变动到0.103,同样在OLS估计下的95%的置信区间内［0.092,0.106］。exper的系数变化很小，black和Hispanic的系数变化很大，但是这些估计值在统计上并不显著。最重要的变化是在-截距估计从［649,539］：从0.649变化到0.539.在本例中，截距为log(wage)的非黑人非西班牙裔妇女且没有受过教育和工作经验的估计值。在全样本下并没有一个妇女是这种情况的。因为斜率系数会发生改变,我们不能说,Heckman估计意味着与没有修止的估计相比，工资水平会更低。C18.5(i)估计的方程如下：hy6t=0.078+1.027hy3t・l-1.021Ahy3t-0.085Ahy3t_i-0.104Ahy3t_2(0.028)(0.016)(0.038)(0.037)(0.037)n=121,R2=0.982,&=o」23.使用t检验原假设H0：P=1的t统计量为(1.027-1)/0.016Q1.69.在5%的显著性水平下的使用双侧检验中，我们不能拒绝H0:p=l,但在10%的水平上我们会拒绝原假设(P=1)。•genchy3_a=chy3［_n-2］(3missingvaluesgenerated)■reghy6hy3_lchy3chy3_lchy3_>—>(4,116；ModelResidual—=1550.5394.3903851.765407411623.5975962.015219026Total96.155792120•801298266Source|SSdfMS>umberofobs=121Prob>F=0.0000R-squared=0.9816AdjR-squared=0.9810RootMSE=」2337hy6Coef・Std.Eh.tP>ltl[95%Conf.Interval]hy3」1.02707.015713465.360.000.99594761.058193chy3-1.021114■0375812■27.170.000・1.095548■•9466792chy3_l-.0854249■0371327-2.300.023-.1589709-.0118789chy3_m-.1043577■0374465-2.790.006-.1785251-.0301902_cons・0775016.02773692.790.006.0225653・132438(ii)估计的误差纠正模型如下:加6/=.070+1.259Ahy3(_i-.816(hy6t_i-hy3(_2)(.049)(.278)(.256)\n+.283Ahy3t-2+.127(hy6t-2-hy3t-3)(.272)(.256)n=121,R2=.795.这两个变量的F检验的联合显著的F值为1.35,相应的p•值=0.264,不显著genhy6hy3_T=hy6hy3_l[_n-l]2missingvaluesgenerated)genhy6hy3_q=hy6hy3_l[_n-l]2missingvaluesgenerated)•regchy6chy3_lhy6hy3_Tchy3_>hy6hy3_qlote:hy6hy3_qomittedbecauseofcol1meantySourcessdfMSNumberofobs二121=150.88F\J,丄「丿Model52.1903481317..3967827Prob>F=0.0000Residual13.4902407117.115301202R・squared二0.7946AdjR-squared=0.7893Total65.6805888120.54733824RootMSE=.33956chy6Coef.Std・Err.tp>ltl[95%Conf.Interval]chy3_l1.29504・2673424.840.000.76558311.824497hy6hy3_w-.7823995.246228-3.180.002-1.270041-.2947578chy3_m・1575777.10037481.570.119-.0412093.3563647hy6hy3_q(obitted)_cons.0818882.04306381.900.060・.0033974.1671738■testchy3_>hy6hy3_q(1)chy3_>=0(2)o.hy6hy3_q=0Constraint2droppedF(1,117)=2.46Prob>F=0.1191