《统计学讲义》PPT课件

《统计学讲义》PPT课件

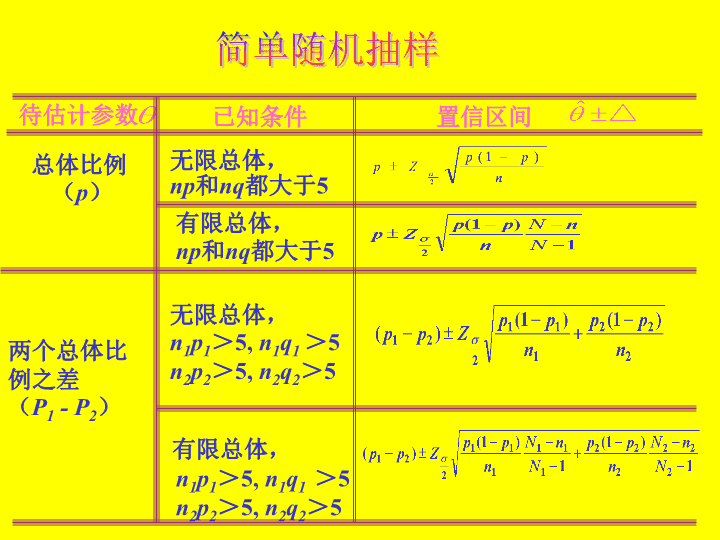
简单随机抽样\n参数的区间估计简单随机抽样待估计参数已知条件置信区间两个正态总体已知两个正态总体未知但相等两个非正态总体,n1，n2≥30两个总体均值之差μ1-μ2\n简单随机抽样待估计参数已知条件置信区间无限总体，np和nq都大于5总体比例（p）无限总体，n1p1＞5,n1q1＞5n2p2＞5,n2q2＞5两个总体比例之差（P1-P2）有限总体，np和nq都大于5有限总体，n1p1＞5,n1q1＞5n2p2＞5,n2q2＞5\n简单随机抽样待估计参数已知条件置信区间正态总体总体方差两个正态总体两个总体方差之比\n例：设某灯泡的寿命X～N（，2），，2未知，现从中任取5个灯泡进行寿命试验，得数据10.5，11.0，11.2，12.5，12.8（单位：千小时），求置信水平为90%的2的区间估计。\n2的置信区间为（0.4195，5.5977）由得查表得解样本方差及均值分别为\n研究由机器A和机器B生产的钢管内径,随设两样本相互独例：机抽取机器A生产的管子18只,测得样本方差为均未知,求方差比的置信度为0.90的置信区间。抽取机器B生产的管子13只,测得样本方差为立,且设由机器A和机器B生产的钢管内径分别服从正态分布\n解\n68.27%95.45%99.73%图4-2正态分布概率图\n课堂练习1.假设参加某种寿险投保人的年龄服从正态分布，标准差为7.77岁。从中抽取36人组成一个简单随机样本，其平均年龄为39.5岁，试建立投保人平均年龄的90%的置信区间。\n\n2.为提高银行的服务质量，管理部门需要考查在柜台上办理每笔业务所需要的服务时间。假设每笔业务所需时间服从正态分布，现从中抽取16笔业务组成一个简单随机样本，其平均服务时间为13分钟，样本标准差为5.6分钟，试建立每笔业务平均服务时间的95%的置信区间。\n\n3.为了解居民用于服装消费的支出情况，随机抽取90户居民组成一个简单随机样本，计算得样本均值为810元，样本标准差为85元，试建立该地区每户居民平均用于服装消费支出的95%的置信区间。\n\n4.某连锁店准备在两个不同地点选择一个地方开一家新店，为此需调查这两个地点居民收入的差别。在甲地点调查了100户居民，年平均收入为19000元，标准差为70元，在乙地点调查了80户居民，年平均收入为17000元，标准差为75元。试建立两个地点居民年平均收入差别的99%的置信区间。\n\n6.对某个电视广告的收视率进行调查。在甲地区调查了200人，有128人收看过该广告，在乙地区调查了225人，有90人收看过该广告。试以90%的可靠性对该广告在两地收视率的差别作出区间估计。\n