统计学 公式 大全

统计学 公式 大全

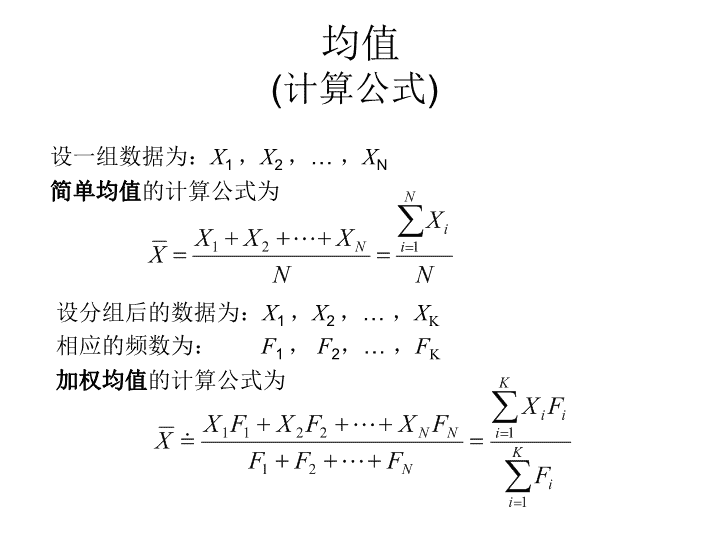
均值(概念要点)1.集中趋势的测度值之一2.最常用的测度值3.一组数据的均衡点所在4.易受极端值的影响5.用于数值型数据，不能用于定类数据和定序数据\n均值(计算公式)设一组数据为：X1，X2，…，XN简单均值的计算公式为设分组后的数据为：X1，X2，…，XK相应的频数为：F1，F2，…，FK加权均值的计算公式为\n均值(数学性质)1.各变量值与均值的离差之和等于零2.各变量值与均值的离差平方和最小\n众数、中位数和均值的关系对称分布均值=中位数=众数左偏分布均值中位数众数右偏分布众数中位数均值\n数据类型与集中趋势测度值表4-4数据类型和所适用的集中趋势测度值数据类型定类数据定序数据定距数据定比数据适用的测度值※众数※中位数※均值※均值—四分位数众数调和平均数—众数中位数几何平均数——四分位数中位数———四分位数———众数\n总体方差和标准差(计算公式)未分组数据：组距分组数据：未分组数据：组距分组数据：方差的计算公式标准差的计算公式\n样本方差和标准差(计算公式)未分组数据：组距分组数据：未分组数据：组距分组数据：方差的计算公式标准差的计算公式\n离散系数(概念要点和计算公式)1.标准差与其相应的均值之比2.消除了数据水平高低和计量单位的影响3.测度了数据的相对离散程度4.用于对不同组别数据离散程度的比较5.计算公式为\n偏态与峰度分布的形状扁平分布尖峰分布偏态峰度左偏分布右偏分布与标准正态分布比较！\n偏态(概念要点)1.数据分布偏斜程度的测度2.偏态系数=0为对称分布3.偏态系数>0为右偏分布4.偏态系数<0为左偏分布5.计算公式为\n峰度(概念要点)1.数据分布扁平程度的测度2.峰度系数=3扁平程度适中3.偏态系数<3为扁平分布4.偏态系数>3为尖峰分布5.计算公式为\n时间序列的分类时间序列平均数序列绝对数序列相对数序列时期序列时点序列\n时间序列的分类绝对数时间序列一系列绝对数按时间顺序排列而成时间序列中最基本的表现形式反映现象在不同时间上所达到的绝对水平分为时期序列和时点序列时期序列：现象在一段时期内总量的排序时点序列：现象在某一瞬间时点上总量的排序相对数时间序列一系列相对数按时间顺序排列而成平均数时间序列一系列平均数按时间顺序排列而成\n绝对数序列的序时平均数（计算方法）计算公式：【例11.1】根据表11.1中的国内生产总值序列，计算各年度的平均国内生产总值时期序列\n绝对数序列的序时平均数（计算方法）时点序列—间隔不相等Y1Y2Y3YnY4Yn-1T1T2T3Tn-1\n绝对数序列的序时平均数（计算方法）计算步骤计算出两个点值之间的平均数用相隔的时期长度(Ti)加权计算总的平均数\n绝对数序列的序时平均数（计算方法）当间隔相等(T1=T2=…=Tn-1)时，有时点序列—间隔相等Y1Y2Y3YnYn-1\n相对数序列的序时平均数（计算方法）先分别求出构成相对数或平均数的分子ai和分母bi的平均数再进行对比，即得相对数或平均数序列的序时平均数基本公式为\n增长量（概念要点）报告期水平与基期水平之差，说明现象在观察期内增长的绝对数量有逐期增长量与累积增长量之分逐期增长量报告期水平与前一期水平之差计算形式为：Δi=Yi-Yi-1(i=1,2,…,n)累积增长量报告期水平与某一固定时期水平之差计算形式为：Δi=Yi-Y0(i=1,2,…,n)各逐期增长量之和等于最末期的累积增长量\n平均增长量（概念要点）1.观察期内各逐期增长量的平均数2.描述现象在观察期内平均增长的数量3.计算公式为\n环比发展速度与定基发展速度（要点）环比发展速度报告期水平与前一期水平之比定基发展速度报告期水平与某一固定时期水平之比\n环比发展速度与定基发展速度（关系）观察期内各环比发展速度的连乘积等于最末期的定基发展速度两个相邻的定基发展速度，用后者除以前者，等于相应的环比发展速度\n增长速度（要点）增长量与基期水平之比又称增长率说明现象的相对增长程度有环比增长速度与定期增长速度之分计算公式为\n环比增长速度与定基增长速度（要点）环比增长速度基报告期水平与前一时期水平之比定基增长速度报告期水平与某一固定时期水平之比\n平均发展速度（要点）观察期内各环比发展速度的平均数说明现象在整个观察期内平均发展变化的程度通常采用几何法(水平法)计算计算公式为\n年度化增长率（要点）增长率以年来表示时，称为年度化增长率或年率可将月度增长率或季度增长率转换为年度增长率计算公式为m为一年中的时期个数；n为所跨的时期总数季度增长率被年度化时，m＝4月增长率被年度化时，m＝12当m＝n时，上述公式就是年增长率\n速度的分析与应用（增长1%绝对值）速度每增长一个百分点而增加的绝对量用于弥补速度分析中的局限性计算公式为甲企业增长1%绝对值＝500/100＝5万元乙企业增长1%绝对值＝60/100＝0.6万元\n时间序列的构成要素与模型（要点）构成因素长期趋势(Seculartrend)季节变动(SeasonalFluctuation)循环波动(CyclicalMovement)不规则波动(IrregularVariations)模型乘法模型：Yi=Ti×Si×Ci×Ii加法模型：Yi=Ti+Si+Ci+Ii\n线性模型法（概念要点与基本形式）现象的发展按线性趋势变化时，可用线性模型表示线性模型的形式为—时间序列的趋势值t—时间标号a—趋势线在Y轴上的截距b—趋势线的斜率，表示时间t变动一个单位时观察值的平均变动数量\n线性模型法（a和b的最小二乘估计）趋势方程中的两个未知常数a和b按最小二乘法(Least-squareMethod）求得根据回归分析中的最小二乘法原理使各实际观察值与趋势值的离差平方和为最小最小二乘法既可以配合趋势直线，也可用于配合趋势曲线根据趋势线计算出各个时期的趋势值\n线性模型法（a和b的最小二乘估计）1.根据最小二乘法得到求解a和b的标准方程为取时间序列的中间时期为原点时有t=0，上式可化简为解得：解得：\n相关关系的测度（相关系数）样本相关系数的计算公式或化简为\n最小二乘法（和的计算公式）根据最小二乘法的要求，可得求解和的标准方程如下\n样本决定系数（判定系数r2）回归平方和占总离差平方和的比例反映回归直线的拟合程度取值范围在[0,1]之间r21，说明回归方程拟合的越好；r20，说明回归方程拟合的越差判定系数等于相关系数的平方，即r2＝(r)2\n指数的概念和性质（概念要点）指数的概念广义：任何两个数值对比形成的相对数狭义：用于测定总体各变量在不同场合下综合变动的一种特殊相对数指数的性质相对性：总体变量在不同场合下对比形成的相对数不同时间上对比形成的指数称为时间性指数不同空间上对比形成的指数称为区域性指数综合性：反映一组变量在不同场合下的综合变动平均性：指数是总体水平的一个代表性数值\n指数的分类指数的分类按计算形式划分按内容划分按项目多少划分数量指数质量指数按对比场合划分时间指数区域指数简单指数加权指数个体指数综合指数\n指数的分类（数量指数与质量指数）数量指数反映物量变动水平如产品产量指数、商品销售量指数等质量指数反映事物内含数量的变动水平如价格指数、产品成本指数等\n指数的分类（个体指数与综合指数）个体指数反映单一项目的变量变动如一种商品的价格或销售量的变动综合指数反映多个项目变量的综合变动如多种商品的价格或销售量的综合变动\n权数的确定（要点）根据现象之间的联系确定权数计算数量指数时，应以相应的质量为权数计算质量指数时，应以相应的物量为权数确定权数的所属时期可以都是基期，也可以都是报告期或某一固定时期使用不同时期的权数，计算结果和意义不同取决于计算指数的预期目的确定权数的具体形式可以是总量形式，也可以采取比重形式主要取决于所依据的数据形式和计算方法\n加权综合指数(概念要点)通过加权来测定一组项目的综合变动有加权数量指数和加权质量指数数量指数测定一组项目的数量变动如产品产量指数，商品销售量指数等质量指数测定一组项目的质量变动如价格指数、产品成本指数等因权数不同，有不同的计算公式\n基期变量值加权的综合指数(要点和计算公式)将作为权数的各变量值固定在基期也被称为拉氏指数或L式指数计算公式为质量指数：数量指数：可以消除权数变动对指数的影响\n报告期变量值加权的综合指数(要点和计算公式)将作为权数的各变量值固定在报告期也被称为帕氏指数，或简称为P式指数计算公式为质量指数：数量指数：不能消除权数变动对指数的影响\n基期总量加权的平均指数(要点和计算公式)以基期总量为权数对个体指数加权平均计算形式上采用算术平均形式计算公式为质量指数：数量指数：\n报告期总量加权的平均指数(要点和计算公式)以报告期总量为权数对个体指数加权平均计算形式上采用调和平均形式计算公式为质量指数：数量指数：\n总量指数(概念要点)由两个不同时期的总量对比可以是实物总量对比，如粮食总产量指数可以是价值总量对比，称为价值指数，如工业总产值、产品总成本、商品销售额指数一般形式个体总量指数：综合总量指数：\n指数体系(概念要点)由总量指数及其若干个因素指数构成的数量关系式总量指数等于各因素指数的乘积总量的变动差额等于各因素指数变动差额之和两个因素指数中通常一个为数量指数，另一个为质量指数各因素指数的权数必须是不同时期的\n加权综合指数体系(要点及公式)因所用权数时期不同，有不同的指数体系比较常用的是基期权数加权的数量指数和报告期权数加权的质量指数形成的指数体系指数体系可表示为相对数关系绝对数关系\n加权平均指数体系(要点及公式)因所用总量权数所属时期不同，有不同的指数体系常用的是基期总量加权算术平均数量指数和报告期总量加权调和平均质量指数形成的指数体系绝对数关系相对数关系\n利用指数体系分析平均数变动(要点及公式)通过两个不同时期的加权算术平均数之比反映现象平均水平的变动通过对加权算术平均数的分解，分析影响平均数变动的各因素\n利用指数体系分析平均数变动(要点及公式)三个指数之间的相对数量关系三个指数之间的绝对数量关系\n利用指数体系分析平均数变动(计算结果及分析)结论1999年同1998年相比，该企业三个车间的劳动生产率均有所提高，但企业总的劳动生产率却下降了2.22%，人均下降0.14万元各车间劳动生产率的提高使企业总的生产率提高了2.66%，人均提高0.16万元各车间职工人数结构的变化，使企业总的劳动生产率下降了4.75%，人均下降0.3万元\n零售价格指数(RetailPriceIndex)反映城乡商品零售价格变动趋势的一种经济指数编制中的主要问题代表规格品的选择典型地区的选择商品价格的确定权数的确定计算公式