统计学实验作业

统计学实验作业

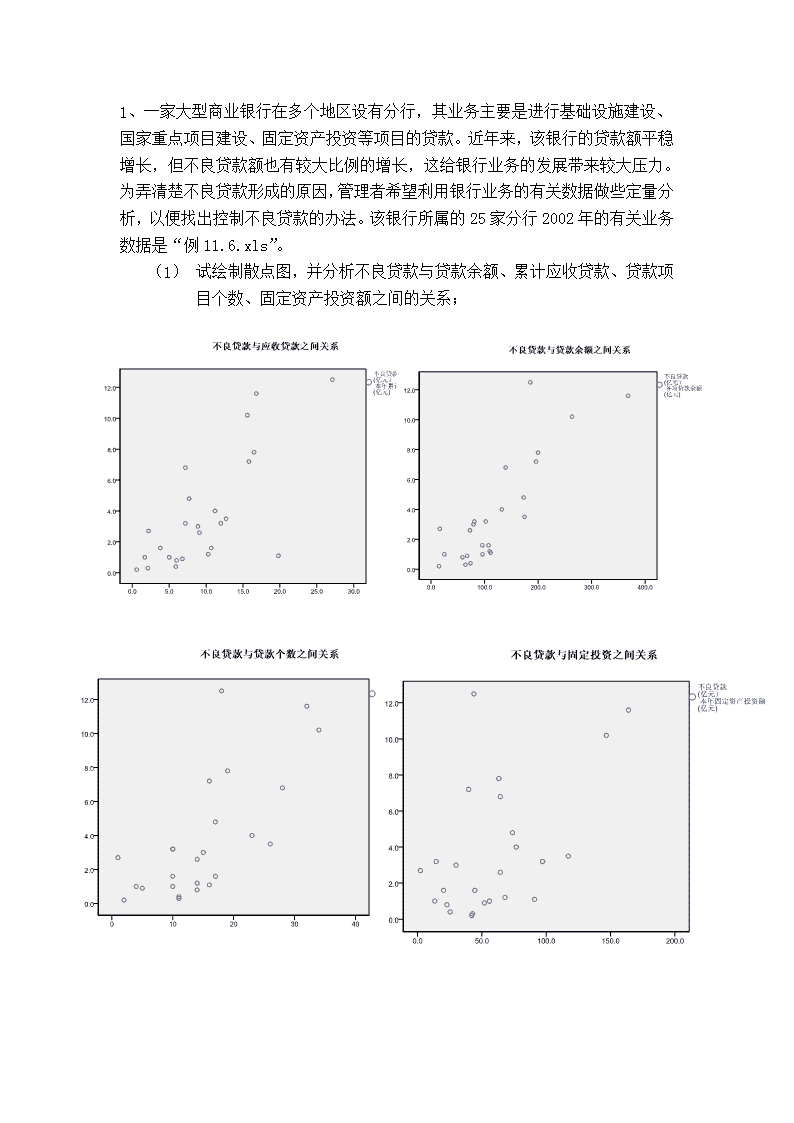
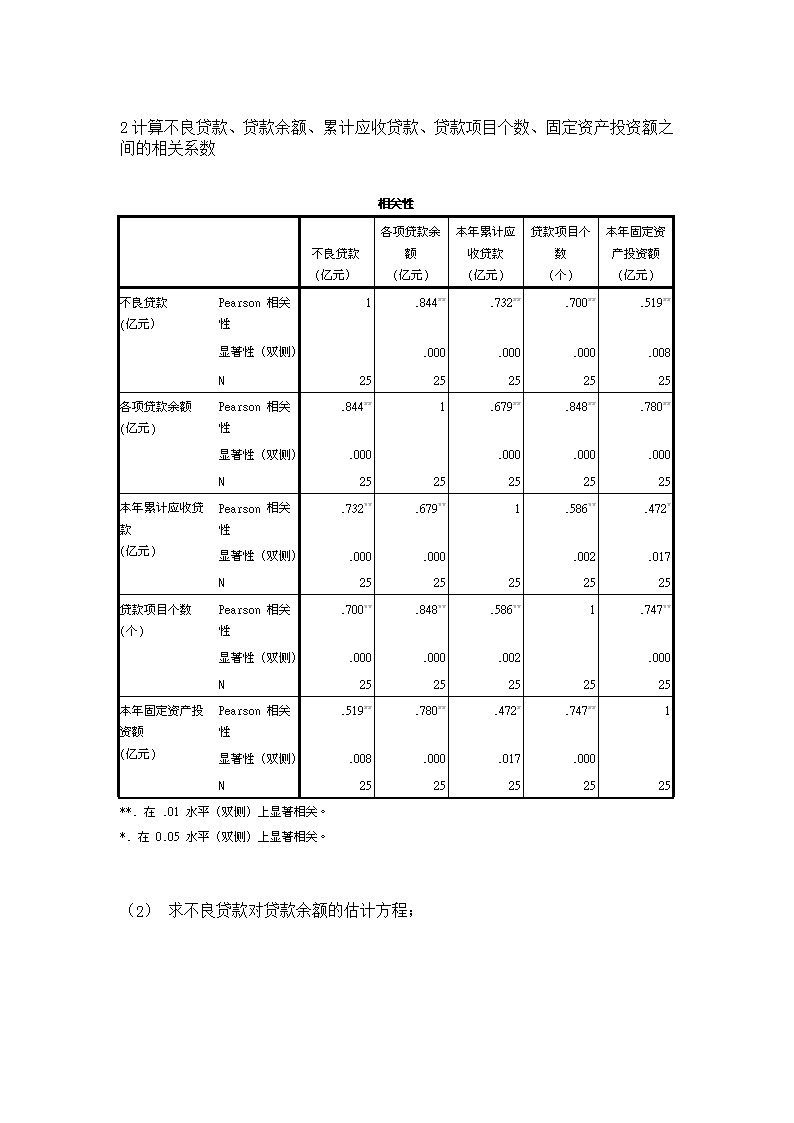
1、一家大型商业银行在多个地区设有分行，其业务主要是进行基础设施建设、国家重点项目建设、固定资产投资等项目的贷款。近年来，该银行的贷款额平稳增长，但不良贷款额也有较大比例的增长，这给银行业务的发展带来较大压力。为弄清楚不良贷款形成的原因，管理者希望利用银行业务的有关数据做些定量分析，以便找出控制不良贷款的办法。该银行所属的25家分行2002年的有关业务数据是“例11.6.xls”。（1）试绘制散点图，并分析不良贷款与贷款余额、累计应收贷款、贷款项目个数、固定资产投资额之间的关系；\n2计算不良贷款、贷款余额、累计应收贷款、贷款项目个数、固定资产投资额之间的相关系数相关性不良贷款(亿元）各项贷款余额(亿元)本年累计应收贷款(亿元)贷款项目个数(个)本年固定资产投资额(亿元)不良贷款(亿元）Pearson相关性1.844**.732**.700**.519**显著性（双侧）.000.000.000.008N2525252525各项贷款余额(亿元)Pearson相关性.844**1.679**.848**.780**显著性（双侧）.000.000.000.000N2525252525本年累计应收贷款(亿元)Pearson相关性.732**.679**1.586**.472*显著性（双侧）.000.000.002.017N2525252525贷款项目个数(个)Pearson相关性.700**.848**.586**1.747**显著性（双侧）.000.000.002.000N2525252525本年固定资产投资额(亿元)Pearson相关性.519**.780**.472*.747**1显著性（双侧）.008.000.017.000N2525252525**.在.01水平（双侧）上显著相关。*.在0.05水平（双侧）上显著相关。（1）求不良贷款对贷款余额的估计方程；\nAnovab模型平方和df均方FSig.1回归249.371462.34319.704.000a残差63.279203.164总计312.65024a.预测变量:(常量),本年固定资产投资额(亿元),本年累计应收贷款(亿元),贷款项目个数(个),各项贷款余额(亿元)。b.因变量:不良贷款(亿元模型汇总模型RR方调整R方标准估计的误差更改统计量R方更改F更改df1df2Sig.F更改1.893a.798.7571.7788.79819.704420.000a.预测变量:(常量),本年固定资产投资额(亿元),本年累计应收贷款(亿元),贷款项目个数(个),各项贷款余额(亿元)。\n系数a模型非标准化系数标准系数tSig.B标准误差试用版1(常量)-1.022.782-1.306.206各项贷款余额(亿元).040.010.8913.837.001本年累计应收贷款(亿元).148.079.2601.879.075贷款项目个数(个).015.083.034.175.863本年固定资产投资额(亿元)-.029.015-.325-1.937.067a.因变量:不良贷款(亿元）从表系数可以看出常量、应收贷款、项目个数、固定资产投资额，都接受原假设，只有贷款余额拒绝原假设，所以只有贷款余额对不良贷款起作用。共线性诊断a模型维数特征值条件索引方差比例(常量)各项贷款余额(亿元)本年累计应收贷款(亿元)贷款项目个数(个)本年固定资产投资额(亿元)114.5381.000.01.00.01.00.002.2034.733.68.03.02.01.093.1575.378.16.00.66.01.134.0668.287.00.09.20.36.725.03611.215.15.87.12.63.05a.因变量:不良贷款(亿元）从共线性可以看出，第五个特征值对贷款余额解释87%，对应收账款解释度为12%、对贷款个数解释度为63%、对固定资产投资解释度为5%。所以不是太共线。、线性方程为Y=0.01XY为不良贷款,X为贷款余额。\n4检验不良贷款与贷款余额之间线性关系的显著性（α=0.05）；回归系数的显著性（α=0.05）；回归系数a模型非标准化系数标准系数tSig.共线性统计量B标准误差试用版容差VIF1(常量)-.830.723-1.147.263各项贷款余额(亿元).038.005.8447.534.0001.0001.000a.因变量:不良贷款(亿元）共线性诊断a模型维数特征值条件索引方差比例(常量)各项贷款余额(亿元)111.8371.000.08.082.1633.354.92.92a.因变量:不良贷款(亿元）通过对上表分析得出：贷款余额线性关系通过显著性检验，回归系数通过显著性检验。5绘制不良贷款与贷款余额回归的残差图。\n2.练习《统计学》教材P330练习题11.1、11.6、11.7、11.8、11.15，对应的数据文件为“习题11.1.xls”、“习题11.6.xls”、“习题11.7.xls”、“习题11.8.xls”、“习题11.15.xls”。(任选两题)11.1（1）绘制产量与生产费用之间的散点图，判断二者之间的关系形态.\n正向相关（1）计算产量与生产费用之间的线性相关系数相关性产量（台）生产费用（万元）产量（台）Pearson相关性1.920**显著性（双侧）.000N1212生产费用（万元）Pearson相关性.920**1显著性（双侧）.000N1212**.在.01水平（双侧）上显著相关。答：产量与生产费用之间的线性相关系数为0.92（3）对相关系数的显著性进行检验，并说明二者间的关系强度模型汇总模型RR方调整R方标准估计的误差更改统计量R方更改F更改df1df2Sig.F更改1.920a.847.83214.791.84755.286110.000a.预测变量:(常量),生产费用（万元）。答：二者的关系强度为92%，P值较小拒绝原假设所以关系强11.8设月租金为自变量，出租率为因变量，回归并对结果进行解释和分析。\n模型汇总模型RR方调整R方标准估计的误差1.795a.632.6122.6858a.预测变量:(常量),每平方米月租金（元）。Anovab模型平方和df均方FSig.1回归223.1401223.14030.933.000a残差129.845187.214总计352.98619a.预测变量:(常量),每平方米月租金（元）。b.因变量:出租率（%）\n系数a模型非标准化系数标准系数tSig.B标准误差试用版1(常量)49.3183.80512.961.000每平方米月租金（元）.249.045.7955.562.000a.因变量:出租率（%）回归方程为Y=49.318+0.249X常量与每平米月租金都通过显著性检验，拒绝原假设所以方程成立。相关系数为0.795中度相关。