- 2021-06-15 发布 |
- 37.5 KB |
- 26页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中理科数学大题
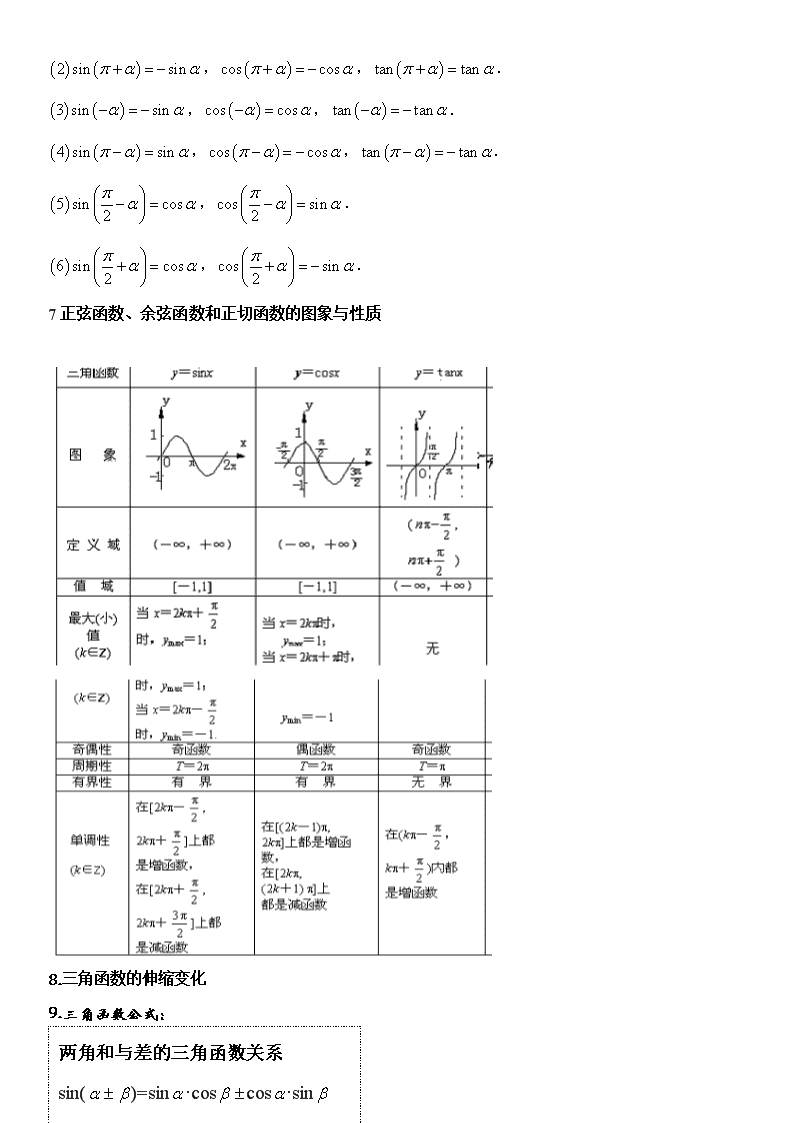
三角函数 一 知识点总结 1.角度制与弧度制的互化: ,23600 ,1800 1rad= 180 °≈57.30°=57°18ˊ. 1°= 180 ≈0.01745(rad) 2.弧长及扇形面积公式 弧长公式: rl . 扇形面积公式:S= rl.2 1 ----是圆心角且为弧度制。 r-----是扇形半径 3.任意角的三角函数 设 是一个任意角,它的终边上一点 p(x,y), r= 22 yx (1)正弦 sin = r y 余弦 cos = r x 正切 tan = x y (2)各象限的符号: x y + O — — + x y O — + — + y O sin cos tan 4、三角函数线 正弦线:MP; 余弦线:OM; 正切线: AT. 5.同角三角函数的基本关系: (1)平方关系:sin2 + cos2 =1。 (2)商数关系: cos sin =tan ( zkk ,2 ) 6.诱导公式:奇变偶不变,符号看象限 1 sin 2 sink , cos 2 cosk , tan 2 tank k . — + + — � T � M � A � O � P � x � y 2 sin sin , cos cos , tan tan . 3 sin sin , cos cos , tan tan . 4 sin sin , cos cos , tan tan . 5 sin cos2 ,cos sin2 . 6 sin cos2 ,cos sin2 . 7 正弦函数、余弦函数和正切函数的图象与性质 8.三角函数的伸缩变化 9.三角函数公式: 两角和与差的三角函数关系 sin( )=sin ·cos cos ·sin cos( )=cos ·cos sin ·sin 10.正弦定理 : 2sin sin sin a b c RA B C . 11.余弦定理: 2 2 2 2 cosa b c bc A ; 2 2 2 2 cosb c a ca B ; 2 2 2 2 cosc a b ab C . 三角形面积定理. 1 1 1sin sin sin2 2 2S ab C bc A ca B . 二 、三角函数常考题型 三角函数题是高考数学试卷的第一道解答题,试题难度一般不大,但其战略意义重大,所以稳拿 该题 12 分对文理科学生都至关重要。分析近年高考试卷,可以发现,三角解答题多数喜欢和平面向 量综合在一起,且向量为辅,三角为主,主要有以下三类: 一、运用同角三角函数关系、诱导公式、和、差、倍、半等公式进行化简求值类。 倍角公式 sin2 =2sin ·cos cos2 =cos2 -sin2 =2cos2 -1 =1-2sin2 2tan1 tan22tan 例 1 已知向量 3 3(cos ,sin ), (cos , sin ), [ , ]2 2 2 2 2 x xx x x 且a b 。 (1)若| | 3 a b ,求 x 的取值范围; (2)函数 ( ) | |f x a b a b ,若对任意 1 2, [ , ]2x x ,恒有 1 2| ( ) ( ) |f x f x t ,求t 的取值范围。 解:(1) | | | | 1, cos2 , | | 2 2cos2 2cos 3x x x a b a b a b , 即 3 5cos . [ , ],2 2 6x x x 。 (2) 21 3( ) | | cos2 2cos 2(cos )2 2f x x x x a b a b 。 max min1 cos 0, ( ) 3, ( ) 1x f x f x ,又 1 2 max min| ( ) ( ) | ( ) ( ) 4, 4f x f x f x f x t 二、运用三角函数性质解题,通常考查正弦、余弦函数的单调性、周期性、最值、对称轴及对称中 心。 例 3 已知向量 (sina , )2 1 , 1(b , )cos2 , 5 1ba , )2,0( (1)求 sin2sin 及 的值; (2)设函数 xxxf 2cos2)22sin(5)( ])2,24[( x ,求 x 为何值时, )(xf 取得最大值,最大 值是多少,并求 )(xf 的单调增区间。 解:(1) 5 1cossin ba , 25 12sin1)cos(sin 2 ,∴ 25 242sin , 25 492sin1)cos(sin 2 ,∴ 5 7cossin ,∴ 5 3cos , 5 4sin . (2) 12cos)sin2sincos2(cos52cos1)2cos(5)( xxxxxxf 12sin42cos412cos)2sin5 42cos5 3(5 xxxxx 1)42sin(24 x ,∵ 224 x , ∴ 4 5 423 x ,∴当 24 x 时, 621)24()(max fxf ,要使 )(xfy 单调递增, ∴ kxk 224222 , Z)(88 3 kkxk ,又 ]2,24[ x , ∴ )(xfy 的 单 调 增 区间 为 ]8,24[ . 三、解三角形问题,判断三角形形状,正余弦定理的应用。 例 6 在△ ABC 中,角 A,B , C 的对边分别为 a, b ,c.已知向量 ( , )a c b a m , ( , )a c b n ,且 m n . (1)求角C 的大小; (2)若 6sin sin 2A B ,求角 A 的值。 解: (1)由 m n 得( )( ) ( ) 0a c a c b a b ; 整理得 2 2 2 0a b c ab . 即 2 2 2a b c ab ,又 2 2 2 1cos 2 2 2 a b c abC ab ab .又因为0 C ,所以 3C . (2)因为 3C ,所以 2 3A B , 故 2 3B A . 由 6 2 6sin sin , sin sin( )2 3 2A B A A 得 .即 3 1 6sin cos sin2 2 2A A A , 所以 3sin cos 2A A .即 2sin( )6 2A .因为 20 3A ,所以 5 6 6 6A , 故 6 4A 或 3 6 4A ,∴ 12A 或 7 12A . 三角函数的小题涉及三角函数的所有知识点,因此,熟练掌握公式和性质是解好小题的必要条件, 在日常训练中一定要改掉边做题边看公式的坏习惯。再者,填空题答案书写的规范也需反复强调。 数列 一、知识点 1、数列的通项公式与前 n 项的和的关系 1 1 , 1 , 2n n n s na s s n ( 数列{ }na 的前 n 项的和为 1 2n ns a a a ). 2、等差数列的通项公式 * 1 1( 1) ( )na a n d dn a d n N ; 3、等差数列其前 n 项和公式为 1( ) 2 n n n a as 1 ( 1) 2 n nna d 2 1 1( )2 2 d n a d n . 4、等比数列的通项公式 1 *1 1 ( )n n n aa a q q n Nq ; 5、等比数列前 n 项的和公式为 1 1 (1 ) , 11 , 1 n n a q qs q na q 或 1 1 , 11 , 1 n n a a q qqs na q . 二、高考常见题型 题型一:数列的通项公式的求法 A、定义法:①等差数列通项公式;②等比数列通项公式。 B、公式法:已知 nS (即 1 2 ( )na a a f n )求 na ,用作差法: 1 1 ,( 1) ,( 2)n n n S na S S n 。 例.已知数列 na 的前 n 项和 nS 满足 1,)1(2 naS n nn .求数列 na 的通项公式。 解:由 112 1111 aaSa 当 2n 时,有 ,)1(2)(2 11 n nnnnn aaSSa 1 12 2 ( 1) ,n n na a ,)1(22 2 21 n nn aa ……, .22 12 aa 1 1 2 2 1 12 2 ( 1) 2 ( 1) 2 ( 1)n n n n na a ].)1(2[3 2 3 ])2(1[2)1(2 )]2()2()2[()1(2 12 1 1 211 nn n nn nnnn 经验证 11 a 也满足上式,所以 ])1(2[3 2 12 nn na C、累加法: 若 1 ( )n na a f n 求 na : 1 1 2 2 1( ) ( ) ( )n n n n na a a a a a a 1a ( 2)n 。 D、累乘法:已知 1 ( )n n a f na 求 na ,用累乘法: 1 2 1 1 2 1 n n n n n a a aa aa a a ( 2)n 。 E、已知递推关系求 na ,用构造法(构造等差、等比数列)。 ① nf 为常数,即递推公式为 qpaa nn 1 (其中 p,q 均为常数, )0)1(( ppq )。 解法:转化为: )(1 tapta nn ,其中 p qt 1 ,再利用换元法转化为等比数列求解。 例. 已知数列 na 中, 11 a , 321 nn aa ,求 na . 解:设递推公式 321 nn aa 可以转化为 )(21 tata nn 即 321 ttaa nn .故递推公式为 )3(231 nn aa ,令 3 nn ab ,则 4311 ab ,且 23 311 n n n n a a b b .所以 nb 是以 41 b 为首项,2 为公比的等比数列,则 11 224 nn nb , 所以 32 1 n na . 二.数列的前 n 项求和的求法 1.公式法:①等差数列求和公式;②等比数列求和公式, 特别声明:运用等比数列求和公式,务必检查其公比与 1 的关系,必要时需分类讨论. 常用公式: 11 2 3 ( 1)2n n n , 2 2 2 11 2 ( 1)(2 1)6n n n n , 2.分组求和法:在直接运用公式法求和有困难时,常将“和式”中“同类项”先合并在一起,再运用 公式法求和. 3.倒序相加法:若和式中到首尾距离相等的两项和有其共性或数列的通项与组合数相关联,则常可考 虑选用倒序相加法,发挥其共性的作用求和(这也是等差数列前 n 和公式的推导方法). 例 3、求 89sin88sin3sin2sin1sin 22222 的值 解:设 89sin88sin3sin2sin1sin 22222 S …………. ① 将①式右边反序得 1sin2sin3sin88sin89sin 22222 S …………..② (反序) 又因为 1cossin),90cos(sin 22 xxxx ①+②得 (反序相加) )89cos89(sin)2cos2(sin)1cos1(sin2 222222 S =89 ∴ S=44.5 4.错位相减法:如果数列的通项是由一个等差数列的通项与一个等比数列的通项相乘构成,那么常选 用错位相减法(这也是等比数列前 n 和公式的推导方法). 例 4、 求和: 132 )12(7531 n n xnxxxS ………………………① 解:由题可知,{ 1)12( nxn }的通项是等差数列{2n-1}的通项与等比数列{ 1nx }的通项之积 设 n n xnxxxxxS )12(7531 432 ………………………. ② (设制错位) ①-②得 nn n xnxxxxxSx )12(222221)1( 1432 (错位相减) 再利用等比数列的求和公式得: n n n xnx xxSx )12(1 121)1( 1 ∴ 2 1 )1( )1()12()12( x xxnxnS nn n 5.裂项相消法:如果数列的通项可“分裂成两项差”的形式,且相邻项分裂后相关联,那么常选用裂 项相消法求和 常用裂项形式有: ① 1 1 1 ( 1) 1n n n n ;② 1 1 1 1( )( )n n k k n n k ; ③ 2 2 1 1 1 1 1( )1 2 1 1k k k k , 2 1 1 1 1 1 1 1 1 ( 1) ( 1) 1k k k k k k k k k ; ④ 1 1 1 1[ ]( 1)( 2) 2 ( 1) ( 1)( 2)n n n n n n n ;⑤ 1 1 ( 1)! ! ( 1)! n n n n ; 6.通项转换法:先对通项进行变形,发现其内在特征,再运用分组求和法求和。 例 8 、求 1 1111111111 个n 之和. 解:由于 )110(9 199999 11111 11 k kk 个个 (找通项及特征) ∴ 1 1111111111 个n = )110(9 1)110(9 1)110(9 1)110(9 1 321 n (分组求和) = )1111(9 1)10101010(9 1 1 321 个n n = 9110 )110(10 9 1 nn = )91010(81 1 1 nn 导数 一、知识点总结 1、导数的几何意义: 函数 )(xfy 在点 0x 处的导数的几何意义就是曲线 )(xfy 在点 ))(,( 0 xfx 处的切线的斜率,也就是 说,曲线 )(xfy 在点 P ))(,( 0 xfx 处的切线的斜率是 )( 0 ' xf ,切线方程为 ).)(( 0 ' 0 xxxfyy 2.、几种常见函数的导数: ① 'C 0 ;② 1')( nn nxx ; ③ xx cos)(sin ' ;④ xx sin)(cos ' ; ⑤ aaa xx ln)( ' ;⑥ xx ee ')( ; ⑦ axxa ln 1)(log ' ;⑧ xx 1)(ln ' 3、导数的运算法则 (1) ' ' '( )u v u v . (2) ' ' '( )uv u v uv . (3) ' ' ' 2( ) ( 0)u u v uv vv v 4、复合函数的求导法则 设函数 ( )u x 在 点 x 处 有 导 数 ' ' ( )xu x , 函 数 )(ufy 在 点 x 处 的 对 应 点 U 处 有导数 ' ' ( )uy f u ,则复合函数 ( ( ))y f x 在点 x 处有导数,且 ' ' ' x u xy y u ,或写作 ' ' '( ( )) ( ) ( )xf x f u x . 5、极值的判别方法:(极值是在 0x 附近所有的点,都有 )(xf < )( 0xf ,则 )( 0xf 是函数 )(xf 的极大值, 极小值同理) 当函数 )(xf 在点 0x 处连续时, ①如果在 0x 附近的左侧 )(' xf >0,右侧 )(' xf <0,那么 )( 0xf 是极大值; ②如果在 0x 附近的左侧 )(' xf <0,右侧 )(' xf >0,那么 )( 0xf 是极小值 极值与最值区别:极值是在局部对函数值进行比较,最值是在整体区间上对函数值进行比较. 二、常考题型总结 题型一:利用导数研究函数的极值、最值。 1. 3 2( ) 3 2f x x x 在区间 1,1 上的最大值是? 2.已知函数 2)()( 2 xcxxxfy 在 处有极大值,则常数 C? 3.函数 331 xxy 有极小值 ?,极大值? 题型二:利用导数几何意义求切线方程 1.曲线 34y x x 在点 1, 3 处的切线方程是 2y x 2 . 若 曲 线 xxxf 4)( 在 P 点 处 的 切 线 平 行 于 直 线 03 yx , 则 P 点 的 坐 标 为 ( 1 , 0 ) 4.求下列直线的方程: (1)曲线 123 xxy 在 P(-1,1)处的切线; (2)曲线 2xy 过点 P(3,5)的切线; 解:(1) 123|yk 23 1)1,1( 1x /2/23 -上,在曲线点 -xxyxxyP 所以切线方程为 02 11 yxxy 即, (2)显然点 P(3,5)不在曲线上,所以可设切点为 ),( 00 yxA ,则 2 00 xy ①又函数的导数为 xy 2/ , 所以过 ),( 00 yxA 点的切线的斜率为 0 / 2| 0 xyk xx ,又切线过 ),( 00 yxA 、P(3,5)点,所以有 3 52 0 0 0 x yx ②,由 ①②联立方程组得, 25 5 1 1 0 0 0 0 y x y x 或 ,即切点为(1,1)时,切线斜率为 ;22 01 xk ;当切点为(5,25) 时 , 切 线 斜 率 为 102 02 xk ; 所 以 所 求 的 切 线 有 两 条 , 方 程 分 别 为 2510 12 )5(1025)1(21 xyxyxyxy 或即,或 题型三:利用导数研究函数的单调性,极值、最值 1.已知函数 ))1(,1()(,)( 23 fPxfycbxaxxxf 上的点过曲线 的切线方程为 y=3x+1 (Ⅰ)若函数 2)( xxf 在 处有极值,求 )(xf 的表达式; (Ⅱ)在(Ⅰ)的条件下,求函数 )(xfy 在[-3,1]上的最大值; (Ⅲ)若函数 )(xfy 在区间[-2,1]上单调递增,求实数 b 的取值范围 解:(1)由 .23)(,)( 223 baxxxfcbxaxxxf 求导数得 过 ))1(,1()( fPxfy 上点 的切线方程为: ).1)(23()1(),1)(1()1( xbacbayxffy 即 而过 .13)]1(,1[)( xyfPxfy 的切线方程为上 故 3 02 3 323 ca ba ca ba 即 ∵ 124,0)2(,2)( bafxxfy 故时有极值在 ③ 由①②③得 a=2,b=-4,c=5 ∴ .542)( 23 xxxxf (2) ).2)(23(443)( 2 xxxxxf 当 ;0)(,3 22;0)(,23 xfxxfx 时当时 13)2()(.0)(,13 2 fxfxfx 极大时当 又 )(,4)1( xff 在[-3,1]上最大值是 13。 (3)y=f(x)在[-2,1]上单调递增,又 ,23)( 2 baxxxf 由①知 2a+b=0。 依题意 )(xf 在[-2,1]上恒有 )(xf ≥0,即 .03 2 bbxx ①当 6,03)1()(,16 min bbbfxfbx 时 ; ②当 bbbfxfbx ,0212)2()(,26 min时 ; ③当 .60,012 12)(,162 2 min bbbxfb 则时 综上所述,参数 b 的取值范围是 ),0[ 题型四:利用导数研究函数的图象 1.如右图:是 f(x)的导函数, )(/ xf 的图象如右图所示,则 f(x)的图象只可能是( D ) ① ② (A) (B) (C) (D) 2.函数 的图像为143 1 3 xxy ( A ) x y o 4 -4 2 4 -4 2 -2-2 x y o 4 -4 2 4 -4 2 -2 -2 x y y 4 -4 2 4 -4 2 -2-2 6 66 6 y x -4 -2 o 42 2 4 3.方程 内根的个数为在 )2,0(0762 23 xx ( B ) A、0 B、1 C、2 D、3 题型五:求参数取值范围、恒成立及存在性问题 A、分离常数法 例 1、已知函数 ( ) lnf x x x .(Ⅰ)求 ( )f x 的最小值;(Ⅱ)若对所有 1x 都有 ( ) 1f x ax ,求实数 a 的取值范围. 学科网 解:(Ⅰ) exxfxxf 1,0)(,1ln)(' 解得令 ‘ . 又易知 )上单调递减,,在( exf 1,0)( )上单调递增,,在( exf )( 所以 eefxf 1)1()( 的最小值为 (Ⅱ)依题意,得 ( ) 1f x ax 在[1 ) , 上恒成立,即不等式 1lna x x 对于 [1 )x , 恒成立 (分离 常数). 令 1( ) lng x x x , 则 2 1 1 1 1( ) 1g x x x x x . 当 1x 时,因为 1 1( ) 1 0g x x x , 故 ( )g x 是(1 ) , 上的增函数, 所以 ( )g x 的最小值是 (1) 1g ,所以 a 的取值范围是( 1],. B、与二次函数的性质、单调性、不等式等相联系 求解策略: 1、利用“要使 axf )( 成立,只需使函数的最小值 axf min )( 恒成立即可;要使 axf )( 成立, 只需使函数的最大值 axf max )( 恒成立即可 2、已知函数的单调性及单调区间,则转化为关于导数大于或者小于 0 在给定区间上恒成立的问题 3、利用子空间的思想,即首先求出函数的单调增或减区间,然后让题所给的区间是所求区间的子集 类型 1.参数放在函数表达式上 例1.设函数 Raaxxaxxf 其中86)1(32)( 23 . 的取值范围求上为增函数在若 的值求常数处得极值在若 axf axxf ,)0,()()2( .,3)()1( (1)由 的极值点为时经检验知解得 )(3,3.30)3(' xfxaaf (2)方法1: )1)((66)1(66)( 2' xaxaxaxxf .)0,()(,0. 10,)0,()(,),1(),,()(,1 .),()(,0)1(6)(,1 .,),(),1,()(,1 2 上递增在时综上所述 则上递增在要保证上递增在时当 上递增在恒成立时当 符合条件上递增在时当 xfa axfaxfa xfxxfa axfa 方法 2: 0 01,0 )0,()1()1( )0,(0)( )0,()( ' a ax xx xxaxx xxf xf 从而 上恒成立在即 上恒成立在所以 上递增在因为 方法3. 0 0)0( 02 1 0 02 1 ]0,(6)1(66)( ' 2' a f aa axaxxf 可解得 或故有 上最小值大于或等于零在保证 解题方法总结:求 )(' xf 后,若能因式分解则先因式分解,讨论 )(' xf =0 两根的大小判断函数 )(xf 的 单调性,若不能因式分解可利用函数单调性的充要条件转化为恒成立问题. 类型 2.参数放在区间边界上 例2.已知函数 )(,0)( 23 xfyxdcxbxaxxf 曲线处取得极值在 过原点和点p(-1,2),若曲线 )(xfy 在点 P 处的切线与直线 452 的夹角为xy 且切线的倾斜角为钝角. (1) 求 )(xf 的表达式 (2) 若 )(xf 在区间[2m-1,m+1]上递增,求 m 的取值范围. 略解 (1) 23 3)( xxxf ]2,2 1[]3,( 121 012 121 21 ),0()2,(]1,12[ )0,2(,),0(),2,()()2(363)()2( 2' m mm m mm m mm xfxxxxxf 解得 或所以 的一个子区间或是从而只要保证 上递减在上递增在可知 总结:先判断函数的单调性,再保证问题中的区间是函数单调递增(递减)区间的一个子区间即可. C、已知不等式在某区间上恒成立,求参数的取值范围 类型1.参数放在不等式上 例 3.已知 时都取得极值与在 13 2)( 23 xxcbxaxxxf (1) 求a、b的值及函数 )(xf 的单调区间. (2) 若对 2)(],2,1[ cxfx 不等式 恒成立,求c的取值范围. 略解:(1) 2,2 1 ba 212 2)2(]2,1[)(,2)2(,2 1)1( 2 3)1(,27 22)3 2(13 2023,23)().2( 2 22' ccc,c cfxfcfcf cfcfxxxxxxxf 或解得从而 上的最大值为在所以 且或得由 总结:区间给定情况下,转化为求函数在给定区间上的最值. 类型 2.参数放在区间上 例4.已知三次函数 dcxxaxxf 23 5)( 图象上点(1,8)处的切线经过点(3,0),并且 )(xf 在 x=3 处有 极值. (1) 求 )(xf 的解析式. (2) 当 ),0( mx 时, )(xf >0 恒成立,求实数 m 的取值范围. 分析:(1) 935)( 23 xxxxf ]3,0( ),0(0)(]3,0(),0(0)(3 0)3()(,)(,0)()3,3 1( 9)0()()(,0)()3 1,0(3,3 10)( )3)(13(3103)().2( ' ' 21 ‘ 2' 的取值范围为所以 内恒成立在时当且仅当内不恒成立在时所以当 所以单调递减时当 所以单调递增时当得由 m mxfm,mxfm fxfxfxfx fxf,xfxfxxxxf xxxxxf D、知函数图 象的交点情况,求参数的取值范围. 解题思路:1 画出两个图像,即穿线图和趋势图(先增后减再增或者先减后增再减) 2 由趋势图结合根的个数写不等式(主要看极值与 0 的关系) 3 解不等式 例 5.已知函数 1,13)( 23 xxxbxaxxf 在 处取得极值 (1) 求函数 )(xf 的解析式. (2) 若过点 )2)(,1( mmA 可作曲线 y= )(xf 的三条切线,求实数 m 的取值范围. 略解(1)求得 xxxf 3)( 3 (2)设切点为 33)(),3,( 2' 0 3 00 xxfxxxM 因为 0 2 00 '2 0 3 00 0 2 0 3 0 0 2 00 3 0 2 0 66)(332)( , 0332 )1)(33(3 ),1)(33( xxxgmxxxg xA mxx xxmxx Mxxmy 则设 有三个不同的实数根的方程所以关于可作曲线的三条切线因为过点 即 所以 又切线过点所以切线方程为 )2,3( 230)1( 0)0( 1,0)(,)1,0(,),1(),0,()( 100)( 0 0000 000 ' 的取值范围是所求的实数 解得条件是有三个不同实根的充要的方程所以关于 的极值点为故函数上单调递减在上单调递增在所以 或得由 m mg gx xxxgxg xxxg 总 结 : 从 函数的极值符号及单调性来保证函数图象与 x 轴交点个数. 在文科数学中,涉及到高次函数问题一般可用导数知识解决,只要把导数的几何意义,用导数求函 数的极值及最值,用导数求函数单调性等这些基础知识搞清弄懂,那么,利用导数求参数的取值范围这 个问题即可迎刃而解. 圆锥曲线 一、知识点总结 (一)圆 1、定义:点集{M||OM|=r},其中定点 O 为圆心,定长 r 为半径. 2、方程:(1)标准方程:圆心在 c(a,b),半径为 r 的圆方程是(x-a)2+(y-b)2=r2 圆心在坐标原点,半径为 r 的圆方程是 x2+y2=r2 (2)一般方程:①当 D2+E2-4F>0 时,一元二次方程 x2+y2+Dx+Ey+F=0 叫做圆的一般方程,圆心为 )2,2( ED 半 径 是 2 422 FED 。 配 方 , 将 方 程 x2+y2+Dx+Ey+F=0 化 为 (x+ 2 D )2+(y+ 2 E )2= 4 4F-ED 22 ②当 D2+E2-4F=0 时,方程表示一个点(- 2 D ,- 2 E ); ③当 D2+E2-4F<0 时,方程不表示任何图形. 点与圆的位置关系 已知圆心 C(a,b),半径为 r,点 M 的坐标为(x0,y0),则|MC|<r 点 M 在圆 C 内,|MC|=r 点 M 在圆 C 上,|MC|>r 点 M 在圆 C 内,其中|MC|= 2 0 2 0 b)-(ya)-(x 。 直线和圆的位置关系:①直线和圆有相交、相切、相离三种位置关系:直线与圆相交 有两个公共 点;直线与圆相切 有一个公共点;直线与圆相离 没有公共点。 ②直线和圆的位置关系的判定:(i)判别式法;(ii)利用圆心 C(a,b)到直线 Ax+By+C=0 的距离 22 BA CBbAad 与半径 r 的大小关系来判定。 (二)椭圆、双曲线、抛物线: 椭圆、双曲线、抛物线性质对比 椭圆 双曲线 抛物线 定义 1.到两定点 F1,F2 的距 离 之 和 为 定 值 2a(2a>|F1F2|) 的 点 的 轨 迹 2.与定点和直线的距离 之比为定值 e 的点的轨 迹.(0查看更多