- 2021-06-15 发布 |
- 37.5 KB |
- 7页


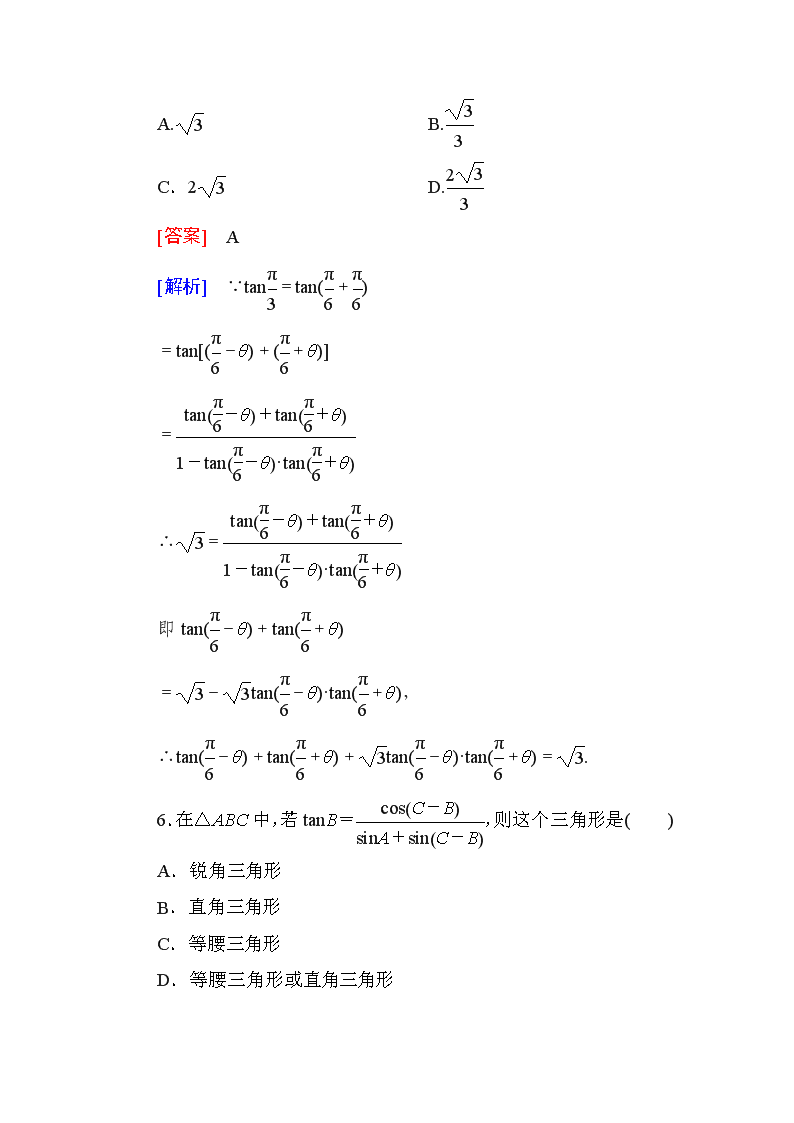
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高一数学(人教A版)必修4能力提升:3-1-2-2 两角和与差的正切
能 力 提 升 一、选择题 1.tan(α+β)=,tan(α-β)=,则tan2α=( ) A. B. C. D. [答案] D [解析] tan2α=tan[(α+β)+(α-β)] ===. 2.(2013长春二模)在△ABC中,若tanAtanB=tanA+tanB+1,则cosC的值是( ) A.- B. C. D.- [答案] B [解析] 由tanA·tanB=tanA+tanB+1,可得=-1,即tan(A+B)=-1,∵A+B∈(0,π),∴A+B=,则C=,cosC=. 3.在△ABC中,若0查看更多
相关文章
- 当前文档收益归属上传用户