高中数学必修1教案：第九章直线平面简单几何体(B)(第34课)小结与复习(1)

高中数学必修1教案：第九章直线平面简单几何体(B)(第34课)小结与复习(1)

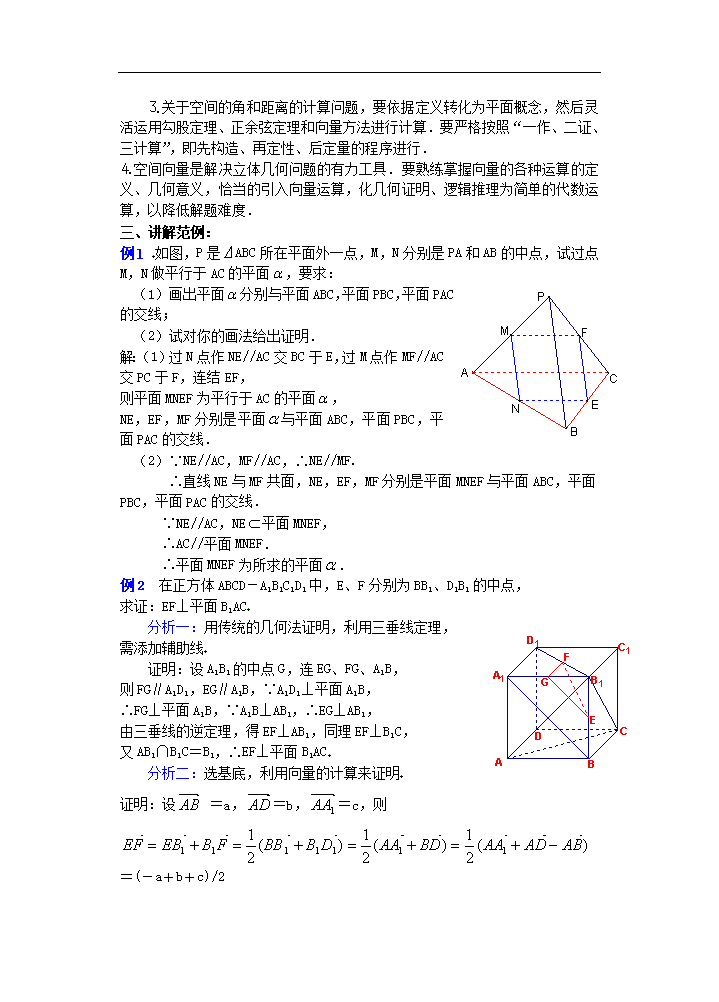
课 题：小结与复习(一) ‎ 教学目的：‎ ‎1以空间的“线线、线面、面面”之间的位置关系为主要线索对所学内容进行横向整理总结这种横纵结合的学习方法有利于对知识的认识更系统、更深入，运用起来更灵活 ‎2．在有关问题的解决过程中，进一步了解和掌握相关公理、定理的内容和功能，并探索立体几何中论证问题的规律；在有关问题的分析与解决的过程中提高逻辑思维能力、空间想象能力及化归和转化的数学思想的应用．‎ ‎3．在解决有关空间角的问题的过程中，进一步巩固关于直线和平面的平行垂直的性质与判定的应用，掌握作平行线(面)和垂直线(面)的技能；通过有关空间角的问题的解决，进一步提高学生的空间想象能力、逻辑推理能力及运算能力．‎ ‎4．通过教学使学生掌握基本的立体几何解题方法和常用解题技巧，发掘不同问题之间的内在联系，提高解题能力．‎ ‎4．在学生解答问题的过程中，注意培养他们的语言表述能力和“说话要有根据”的逻辑思维的习惯、提高思维品质．使学生掌握化归思想，特别是将立体几何问题转化为平面几何问题的思想意识和方法，并提高空间想象能力、推理能力和计算能力．‎ 授课类型：复习课 ‎ 课时安排：1课时 ‎ 教 具：多媒体、实物投影仪 ‎ 教学过程：‎ 一、知识纲要 ㈠空间的直线与平面 ‎⒈平面的基本性质 ‎　⑴三个公理及公理三的三个推论和它们的用途．　⑵斜二测画法．‎ ‎⒉空间两条直线的位置关系：相交直线、平行直线、异面直线．‎ ‎　⑴公理四（平行线的传递性）．等角定理．‎ ‎　⑵异面直线的判定：判定定理、反证法．‎ ‎　⑶异面直线所成的角：定义（求法）、范围．‎ ‎⒊直线和平面平行于平面和平面平行 ‎　⑴直线与平面平行：直线和平面的位置关系、直线和平面平行的判定与性质．‎ ‎　⑵平行平面：两个平面的位置关系、两个平面平行的判定与性质．‎ ‎⒋直线和平面垂直 ‎　⑴直线和平面垂直：定义、判定定理．‎ ‎　⑵三垂线定理及逆定理．‎ ㈡空间向量 ‎⒌空间向量及其运算 ‎　⑴空间向量及其加减与数乘运算（几何方法）．‎ ‎　⑵共线向量定理与共面向量定理．‎ ‎　⑶空间向量基本定理．‎ ‎　⑷两个向量的数量积：定义、几何意义．‎ ‎⒍空间向量的坐标运算 ‎　⑴空间直角坐标系：坐标向量、点的坐标、向量的坐标表示．‎ ‎　⑵向量的直角坐标运算．‎ ‎　⑶夹角和距离公式．‎ ㈢夹角与距离 ‎⒎直线和平面所成的角与二面角 ‎　⑴平面的斜线和平面所成的角：三面角余弦公式、最小角定理、斜线和平 ‎　　面所成的角、直线和平面所成的角．‎ ‎　⑵二面角：①定义、范围、二面角的平面角、直二面角．‎ ‎　　　　　　②互相垂直的平面及其判定定理、性质定理．‎ ‎⒏距离 ‎　⑴点到平面的距离．‎ ‎　⑵直线到与它平行平面的距离．‎ ‎　⑶两个平行平面的距离：两个平行平面的公垂线、公垂线段．‎ ‎　⑷异面直线的距离：异面直线的公垂线及其性质、公垂线段．‎ ㈣简单多面体与球 ‎⒐棱柱与棱锥 ‎　⑴多面体．‎ ‎　⑵棱柱与它的性质：棱柱、直棱柱、正棱柱、棱柱的性质．‎ ‎　⑶平行六面体与长方体：平行六面体、直平行六面体、长方体、正四棱柱、‎ ‎　　正方体；平行六面体的性质、长方体的性质．‎ ‎　⑷棱锥与它的性质：棱锥、正棱锥、棱锥的性质、正棱锥的性质．‎ ‎　⑸直棱柱和正棱锥的直观图的画法．‎ ‎⒑多面体欧拉定理的发现 ‎　⑴简单多面体的欧拉公式．‎ ‎　⑵正多面体．‎ ‎⒒球 ‎　⑴球和它的性质：球体、球面、球的大圆、小圆、球面距离．‎ ‎　⑵球的体积公式和表面积公式．‎ 二、方法总结 ‎⒈解立体几何问题的基本思路：化立体几何问题为平面几何问题．‎ ‎　　⒉熟练掌握所学习的定义、定理，掌握空间直线与直线、直线与平面、平面与平面的相互位置关系的内在联系，灵活的进行互相转化是解立体几何证明题的基础．‎ ‎⒊关于空间的角和距离的计算问题，要依据定义转化为平面概念，然后灵活运用勾股定理、正余弦定理和向量方法进行计算．要严格按照“一作、二证、三计算”，即先构造、再定性、后定量的程序进行．‎ ‎⒋空间向量是解决立体几何问题的有力工具．要熟练掌握向量的各种运算的定义、几何意义，恰当的引入向量运算，化几何证明、逻辑推理为简单的代数运算，以降低解题难度．‎ 三、讲解范例：‎ 例1 如图，P是⊿ABC所在平面外一点，M，N分别是PA和AB的中点，试过点M，N做平行于AC的平面，要求：‎ ‎ （1）画出平面分别与平面ABC，平面PBC，平面PAC的交线；‎ ‎ （2）试对你的画法给出证明．‎ 解：（1）过N点作NE//AC交BC于E，过M点作MF//AC交PC于F，连结EF，‎ 则平面MNEF为平行于AC的平面，‎ NE，EF，MF分别是平面与平面ABC，平面PBC，平面PAC的交线．‎ ‎（2）∵NE//AC，MF//AC，∴NE//MF. ‎ ‎∴直线NE与MF共面，NE，EF，MF分别是平面MNEF与平面ABC，平面PBC，平面PAC的交线．‎ ‎∵NE//AC，NE平面MNEF，‎ ‎∴AC//平面MNEF．‎ ‎∴平面MNEF为所求的平面．‎ 例2　在正方体ABCD－A1B‎1C1D1中，E、F分别为BB1、D1B1的中点，‎ 求证：EF⊥平面B‎1AC 分析一：用传统的几何法证明，利用三垂线定理，‎ 需添加辅助线 ‎　　证明：设A1B1的中点G，连EG、FG、A1B，‎ 则FG∥A1D1，EG∥A1B，∵A1D1⊥平面A1B，‎ ‎∴FG⊥平面A1B，∵A1B⊥AB1，∴EG⊥AB1，‎ 由三垂线的逆定理，得EF⊥AB1，同理EF⊥B‎1C，‎ 又AB1∩B‎1C＝B1，∴EF⊥平面B‎1AC 分析二：选基底，利用向量的计算来证明 证明：设 ＝a，＝b，＝c，则 ‎＝(－a＋b＋c)/2‎ ‎＝a＋b ‎＝(－a＋b＋c)/2•(a＋b)＝(b2－a2＋c•a＋c•b)/2‎ ‎＝(|b|2－|a|2＋0＋0)/2＝0，‎ ‎，即EF⊥AB1，同理EF⊥B‎1C，‎ 又AB1∩B‎1C＝B1，∴EF⊥平面B‎1AC ‎　　分析三：建立空间直角坐标系，利用向量，且将向量的运算转化为实数（坐标）的运算，以达到证明的目的 证明：设正方体的棱长为2，建立如图所示的直角坐标系，‎ 则A(2,0,0),C(0,2,0),B1(2,2,2),E(2,2,1),F(1,1,2),‎ ‎＝(1,1,2)－(2,2,1)＝(―1,―1,1)，‎ ‎＝(2,2,2)－(2,0,0)＝(0,2,2)‎ ‎＝(0,2,0)－(2,0,0)＝(－2,2,0)‎ ‎＝(―1,―1,1)• (0,2,2)＝0‎ ‎＝(―1,―1,1)• (－2,2,0)＝0‎ ‎∴EF⊥AB1， EF⊥AC，又AB1∩B‎1C＝B1，∴EF⊥平面B‎1AC 例3　在四棱锥P－ABCD中，底面ABCD是一直角梯形，∠BAD＝90°，AD∥BC，AB＝BC＝a，AD＝‎2a，且PA⊥底面ABCD，PD与底面成30°（PD和其在底面上的射影所成的角）‎ ‎⑴若AE⊥PD，垂足为E，求证：BE⊥PD；‎ ‎⑵求异面直线AE与CD所成角的大小 解：以A为坐标原点，建立如图所示空间直角坐标系A－xyz，由题意知A(0,0,0),B(a,0,0),C(a,a,0),‎ D(0,‎2a,0)‎ 证明⑴：∵PD在底面上的射影是DA，且PD与底面成30°，∴∠PDA＝30°，‎ ‎∵AE⊥PD，‎ ‎，即BE⊥PD 解⑵：由⑴知 又，‎ ‎∴异面直线AE与CD所成角的大小为arccos 例4 已知空间四边形OABC中，，．求证：．‎ 证明：＝‎ ‎　　　　　　　 ＝－．‎ ‎∵，，‎ ‎∴，，‎ ‎　，．‎ ‎∴，．‎ ‎∴＝，＝0．‎ ‎∴‎ 四、小结 ： 点的坐标与向量的坐标一般不同，只有表示向量的有向线段的起点是坐标原点时.有向线段终点的坐标与向量的坐标相同.这一点务必向学生讲清楚.；明确用向量坐标法证明或计算几何问题的基本步骤：建系设坐标→向量点的坐标化→向量的直角坐标运算 运用向量的坐标表示及其运算研究立体几何中的角、距离、证明垂直等问题时，关键是建立适当的坐标系，进而将向量坐标化，建立坐标系时，要充分利用图形的几何性质掌握运用向量求角、距离的方法 五、课后作业：‎ 六、板书设计（略）‎ 七、课后记：‎