2017-2018学年安徽省铜陵市第一中学高二10月月考数学试题（解析版）

2017-2018学年安徽省铜陵市第一中学高二10月月考数学试题（解析版）

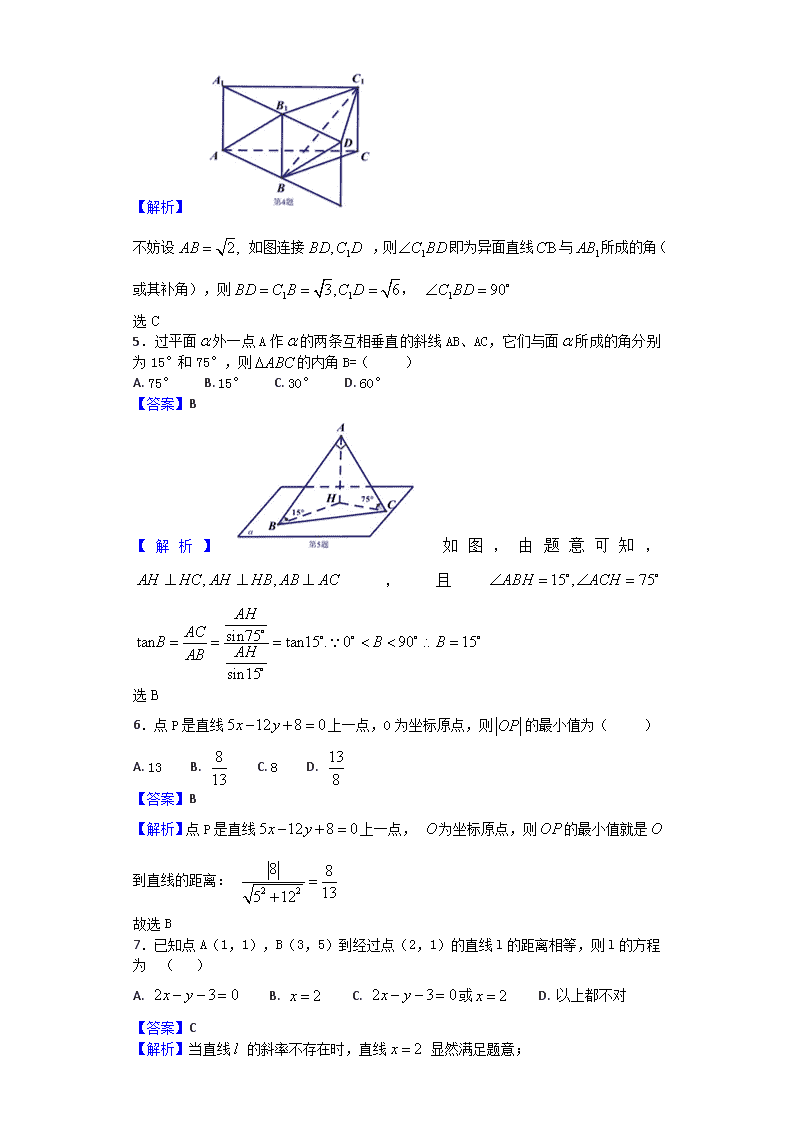
‎2017-2018学年安徽省铜陵市第一中学高二10月月考数学试题 一、单选题 ‎1．已知直线l经过，则直线l的倾斜角为 （ ）‎ A. 20° B. 70° C. 160° D. 110°‎ ‎【答案】D ‎【解析】设直线的倾斜角为 ，则直线的斜率 ‎ 选D ‎2．下列说法不是线面位置关系的性质定理的是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】 A. ，直线和平面垂直的性质定理；‎ B. ，直线与平面平行的性质定理；‎ C. ，直线与平面垂直的判定定理 D ，利用面面垂直判定线面垂直的性质定理 故选C ‎3．已知两条直线与互相平行，则 ( )‎ A. B. -1 C. 1,0 D. -1,0‎ ‎【答案】B ‎【解析】由题两条直线与互相平行，显然 则 ‎ 解得 ，故选B ‎4．在正三棱柱中， ，则异面直线与所成的角是（ ）‎ A. 60° B. 75° C. 90° D. 105°‎ ‎【答案】C ‎【解析】‎ 不妨设 如图连接 ，则即为异面直线与所成的角（或其补角），则， ‎ 选C ‎5．过平面外一点A作的两条互相垂直的斜线AB、AC，它们与面所成的角分别为15°和75°，则的内角B=（ ）‎ A. 75° B. 15° C. 30° D. 60°‎ ‎【答案】B ‎【解析】如图，由题意可知， ，且 ‎ 选B ‎6．点P是直线上一点，O为坐标原点，则的最小值为（ ）‎ A. 13 B. C. 8 D. ‎ ‎【答案】B ‎【解析】点P是直线上一点， 为坐标原点，则的最小值就是到直线的距离： ‎ 故选B ‎7．已知点A（1，1），B（3，5）到经过点（2，1）的直线l的距离相等，则l的方程为 （ ）‎ A. B. C. 或 D. 以上都不对 ‎【答案】C ‎【解析】当直线 的斜率不存在时，直线 显然满足题意； ‎ 当直线的斜率垂存在时，设直线的斜率为 则直线为 ，即 由 到直线的距离等于到直线的距离得：‎ ‎ ，化简得： 或 （无解），解得 所以直线的方程为 综上，直线的方程为或 ． 故选C ‎【点睛】此题考查点到直线的距离公式．解题时容易把斜率不存在的情况遗漏，做题时应充分注意 ‎8．四面体ABCD的棱长AB=CD=6，其余棱长均为，则该四面体外接球半径为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】如图，将四面体还原长方体，其棱长分别为 ，则该四面体外接球半径 ‎ ‎9．在四棱锥P-ABCD中，底面ABCD是平行四边形，E是PC中点，则平面ABE分该四棱锥的两部分的体积比是（ ）‎ A. 2:3 B. 2:5 C. 3:5 D. 3:8‎ ‎【答案】C ‎【解析】如图所示， ，则平面 分该四棱锥的两部分的体积比是，故选C ‎10．在三棱锥P-ABC中，PA⊥面ABC，AB⊥AC且AC=1，AB=2，PA=3，过AB作截面交PC于D，则截面ABD的最小面积为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】如图所示，当时 ，截面ABD的面积最小，此时应有 ‎ 故选C ‎11．设点M是棱长为2的正方体的棱AD的中点，P是平面内一点，若面分别与面ABCD和面所成的锐二面角相等，则长度的最小值是（ ）‎ A. B. C. D. 1‎ ‎【答案】A ‎【解析】如图，过点 作 的平行线交 于点 、交 于点 ，连接 ， 则 是平面 与平面 的交线， 是平面 与平面 的交线． ，交 于点 ，过点作 垂直 于点 ，则有与平面 垂直， 所以， ，即角 是平面 与平面 的所成二面角的平面角， 且 ‎ ‎ 交 于点，过点 作 于点， 同上有： ，且有 ，又因为 ，故 而 ，故 ， 而四边形 一定是平行四边形，故它还是菱形，即点 一定是 的中点， 点 长度的最小值是点 到直线 的距离， 以 为原点， 为 轴， 为 轴， 为 轴，建立空间直角坐标系， ‎ ‎∴ 长度的最小值 ‎ 故选A．‎ ‎【点睛】本题考查空间中两点间最小距离的求法，考查推理论证能力、运算求解能力、空间想象能力，对学生化归与转化思想、数形结合思想有较高要求 ‎12．已知异面直线a,b成70°角，A为空间中一点，则过A且a,b都成55°的平面个数有（ ）‎ A. 1 B. 2 C. 3 D. 4‎ ‎【答案】A ‎【解析】过作 ，设直线 确定的平面为 ， ∵异面直线 成 角，∴直线 确所成锐角为． 设过 点的平面 与所成的角相等，该平面的垂线与直线都成 角，过 只能作一条这样的垂线，故此时符合条件的平面只有一个．‎ 选A 二、填空题 ‎13．已知直线l经过A（-1，2）且原点到直线l的距离为1，则l的方程为__________.‎ ‎【答案】或 ‎【解析】当直线斜率不存在时，方程为 ，当然满足到原点的距离为1； 当直线斜率存在时，设方程为 ，即 ， 由点到直线的距离公式可得 ，解之可得 ‎ 故方程为 故答案为： 或 ‎14．一个几何体的三视图如图，则它的体积为__________.‎ ‎【答案】36‎ ‎【解析】如图所，该几何体为一个三棱柱和一个长方体的组合体，它的体积为 ‎ 即答案为69‎ ‎15．已知二面角 为60°，P为二面角内一点，PA ，PB ，垂足分别为A和B且PA=PB=3，则P到棱l的距离为___________.‎ ‎【答案】6‎ ‎【解析】‎ ‎ 如图所示， 与 确定平面 ，与 交于点 ，则 即为二面角的平面角， ，从而即为所求， ‎ ‎16．在三棱锥A-BCD中， ‎ ‎，点P到三个侧面的距离均等于，则PA=__________.‎ ‎【答案】3‎ ‎【解析】分别在 上取点 使得 且三棱锥外接于半径为 的球 ‎ 三、解答题 ‎17．已知直线垂直于直线，且在两坐标轴上的截距之和为-2，求直线l的方程.‎ ‎【答案】‎ ‎【解析】试题分析：根据垂直条件得出直线的斜率，设出直线的截距式方程，两坐标轴上截距之和为-2，求出两个截距，确定直线 的方程．‎ 试题解析;设，令，令 由题意知： 故 ‎18．在四棱锥P-ABCD中，PA⊥面ABCD， 是PC中点.‎ ‎(1)求证：BE//面PAD；‎ ‎（2）求证：BE⊥面PCD.‎ ‎【答案】(1)证明见解析；(2)证明见解析.‎ ‎【解析】试题分析：（1）取 的中点F，连接 为 中点，证明四边形 为平行四边形，推出 ，然后证明 ‎ ‎（2）首先证明，然后证明，即可得到 试题解析;: ‎ 证明：（1）取PD中点F，连接EF，AF，则 ‎(2)由题意知： ‎ ‎19．如图，在三棱锥P-ABC中，PB⊥AC，PB与底面ABC成30°角， 的面积为1.‎ ‎(1)若PC⊥AB，求证：P在底面ABC的射影H是的垂心;‎ ‎(2)当二面角P-AC-B为多少时， 的面积最大？‎ ‎【答案】(1)证明见解析；(2) .‎ ‎【解析】试题分析：（1）设法证明，同理：AB⊥CH，所以H为的垂心；‎ ‎(2)将问题转化为 而，可求出， 的面积的最大值 试题解析：（1）证明：由题意知： ‎ 同理：AB⊥CH，所以H为的垂心；‎ ‎(2)过B作BD⊥AC于D，连接PD，由（1）知：∠PDB即为二面角P-AC-B的平面角，记∠PDB= ，‎ 在中， ‎ 当且仅当时等号成立.‎ ‎20．已知直线l经过点P（2，2）且分别与x轴正半轴，y轴正半轴交于A、B两点，O为坐标原点.‎ ‎(1)求面积的最小值及此时直线l的方程；‎ ‎(2)求的最小值及此时直线l的方程.‎ ‎【答案】(1)8， ；(2)8； .‎ ‎【解析】试题分析; 设，则 ‎(1) ，当且仅当时，等号成立，即 ‎(2) ，当且仅当 试题解析 :设，则 ‎(1) ，当且仅当时，等号成立，即 ‎(2) ‎ ‎ ，当且仅当时等号成立，即 ‎【点睛】本题给出直线经过定点，求满足特殊条件的直线方程，着重考查了直线的基本量与基本形式、基本不等式求最值等知识，其中设出直线方程转化为是解题的关键 ‎21．在边长为2的正方体中，M是棱CC1的中点.‎ ‎(1)求B到面的距离；‎ ‎(2)求BC与面所成角的正切值；‎ ‎(3)求面与面ABCD所成的锐二面角的余弦值.‎ ‎【答案】(1) ；(2) ；(3) .‎ ‎【解析】试题分析：（1）法1 ，利用等体积法易求 法2 作出并证明 即为到面的距离.‎ ‎(2)设B1M和AM的延长线相交于G，由（1）知即为所求.‎ ‎(3)法1 过B作BE⊥AN，垂足为E，连接B1E，则即为所求.‎ 法2 取A1D1中点F，连接BF，则∠FBB1即为所求.‎ 法3 .‎ 试题解析：（1）法1 ‎ 法2 连接A1B交AB1于E，D1C交MN于F，连接EF，过B作BH⊥EF，垂足为H，则BH即为所求.‎ 如图，易知：BH=.‎ ‎(2)设B1M和AM的延长线相交于G，由（1）知即为所求.‎ ‎(3)法1 过B作BE⊥AN，垂足为E，连接B1E，则即为所求.‎ 法2 取A1D1中点F，连接BF，则∠FBB1即为所求.‎ 法3 .‎ ‎22．如图，在四棱锥P-ABCD中，底面ABCD为菱形，PA⊥面ABCD，PA=AB=2， .‎ ‎(1)求证：面PBD⊥面PAC；‎ ‎(2)求AC与PB所成角的余弦值；‎ ‎(3)求二面角的余弦值.‎ ‎【答案】(1)证明见解析；(2) ；(3) .‎ ‎【解析】试题分析; （1）推导出 ，从而 ，由此能证明平面 ‎ 法1：如图由余弦定理可求 ‎ 法2‎ ‎(3)过B作BF⊥PC，垂足为F，连接DF可知 即为所求，由余弦定理可得二面角的余弦值.‎ 试题解析：．(1)证明： ‎ 又 ‎(2)法1：如图 法2‎ ‎(3)过B作BF⊥PC，垂足为F，连接DF 由（1）知：BD⊥PC，所以，则 ‎∠BFD即为所求，BD=DF=‎ ‎【点睛】本题考查面面垂直的证明，考查两条异面直线所成的角以及二面角的求法，解题时要认真审题，注意空间思维能力的培养．‎