四川省巴中市2021届高三零诊考试数学（文）试题 答案

四川省巴中市2021届高三零诊考试数学（文）试题 答案

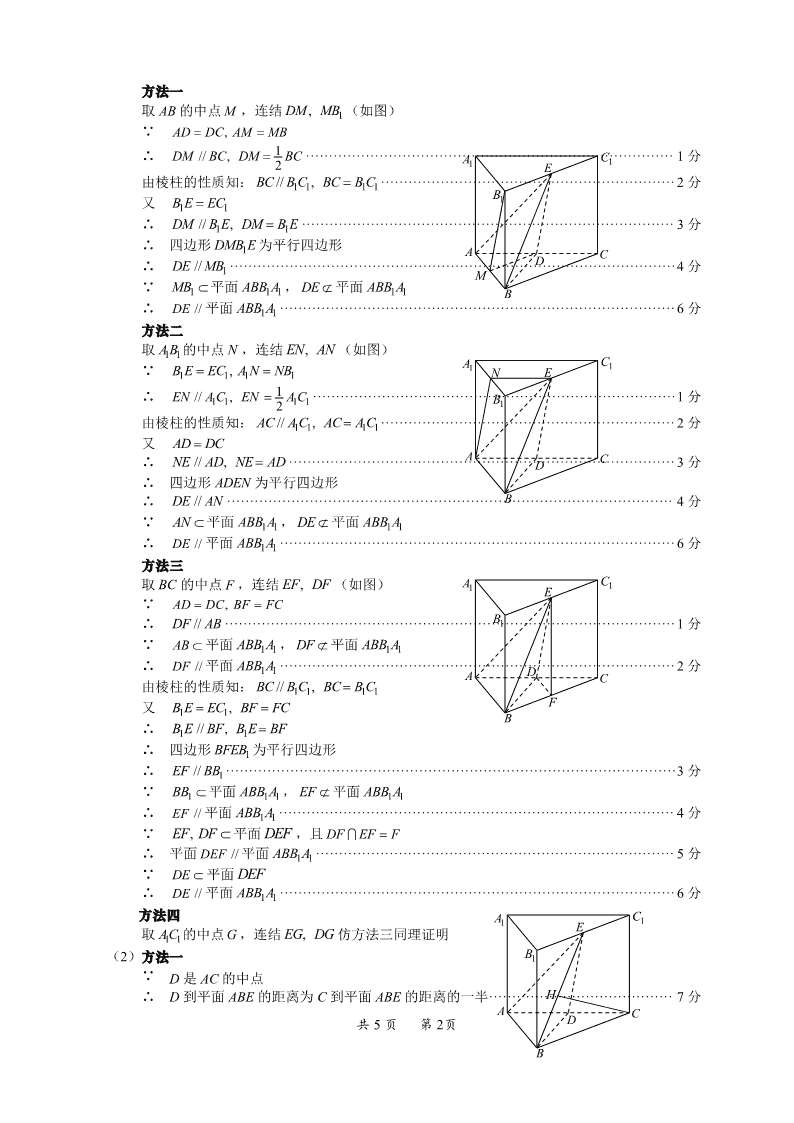
共 5 页 第 1页 巴中市高 2018 级“零诊”考试文科数学 参考答案及评分细则 一、选择题（每小题 5 分，共 60 分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D B D A A B C C B C B A 二、填空题（每小题 5 分，共 20 分） 13. 0 0 00, sinx x x  ≥ 14. 3 15. 32 16. ②③④ 三、解答题（共 70 分） 17、解： （1）由 1 1 2 2n n na a     变形得： 122 1 1   n n n n aa ····························································3 分 又 21 a ，故 1 12 a  ·························································································· 4 分 ∴ 数列{ } 2 n n a 是以 1 为首项 1 为公差的等差数列。·················································5 分 （2）由（1）知： nab n n n  2 ·················································································· 6 分 ∴ 1 1 1 1 1 ( 1) 1n nb b n n n n     ············································································ 8 分 ∴ 1 2 2 3 1 1 1 1 1 1 1 1 1(1 ) ( ) ( )2 2 3 1n nb b b b b b n n             ·······························10 分 = 11 11  n ··························································· 11 分 ∴ 1 2 2 3 1 1 1 1 1 n nb b b b b b      ········································································· 12 分 18、解： （1）这一天小王朋友圈中好友走路步数的平均数 60 140 100 60 20 18 22 6 10 14 18 22 30 9.04400 400 400 400 400 400 400              千步 所以这一天小王 400 名好友走路的平均步数约为 9.04 千步。···································· 3 分 （2）因频率约等概率可得 ( ) 1 9.04 8(60 140 100) 0.565400 4AP      所以事件 A 的概率约为 0.565············································································· 7 分 （3） 健步达人 非健步达人 合计 40 岁以上 150 50 200 不超过 40 岁 50 150 200 合计 200 200 400 2 2 22 4 400(150 50 ) 100 10.828 200 K    所以有 99.9%以上的把握认为健步达人与年龄有关。·············································· 12 分 19、解： （1）证明： 共 5 页 第 2页 方法一 取 AB 的中点 M ，连结 1, DM MB （如图） ∵ , AD DC AM MB  ∴ 1// , 2DM BC DM BC ················································································ 1 分 由棱柱的性质知： 1 1 1 1// , BC B C BC B C ································································2 分 又 1 1B E EC ∴ 1 1// , DM B E DM B E ················································································· 3 分 ∴ 四边形 1DMB E 为平行四边形 ∴ 1//DE MB ·································································································4 分 ∵ 1MB  平面 1 1ABB A ， DE  平面 1 1ABB A ∴ //DE 平面 1 1ABB A ······················································································6 分 方法二 取 1 1AB 的中点 N ，连结 , EN AN （如图） ∵ 1 1 1 1, B E EC A N NB  ∴ 1 1 1 1 1// , 2EN A C EN A C ···············································································1 分 由棱柱的性质知： 1 1 1 1// , AC AC AC AC ································································2 分 又 AD DC ∴ // , NE AD NE AD ····················································································3 分 ∴ 四边形 ADEN 为平行四边形 ∴ //DE AN ································································································· 4 分 ∵ AN  平面 1 1ABB A ， DE  平面 1 1ABB A ∴ //DE 平面 1 1ABB A ······················································································6 分 方法三 取 BC 的中点 F ，连结 , EF DF （如图） ∵ , AD DC BF FC  ∴ //DF AB ··································································································1 分 ∵ AB  平面 1 1ABB A ， DF  平面 1 1ABB A ∴ //DF 平面 1 1ABB A ······················································································2 分 由棱柱的性质知： 1 1 1 1// , BC B C BC B C 又 1 1, B E EC BF FC  ∴ 1 1// , B E BF B E BF ∴ 四边形 1BFEB 为平行四边形 ∴ 1//EF BB ··································································································3 分 ∵ 1BB  平面 1 1ABB A ， EF  平面 1 1ABB A ∴ //EF 平面 1 1ABB A ······················································································ 4 分 ∵ , EF DF  平面 DEF ，且 DF EF F ∴ 平面 //DEF 平面 1 1ABB A ·············································································· 5 分 ∵ DE  平面 DEF ∴ //DE 平面 1 1ABB A ······················································································6 分 方法四 取 1 1AC 的中点 G ，连结 , EG DG 仿方法三同理证明 （2）方法一 ∵ D 是 AC 的中点 ∴ D 到平面 ABE 的距离为 C 到平面 ABE 的距离的一半········································ 7 分 D B A C E 1B 1A 1C M D B A C E 1B 1A 1C N F B A C E 1B 1A 1C D D B A C E 1B 1A 1C H 共 5 页 第 3页 过点 C 作 CH BE 交 BE 于 H 在直三棱柱 1 1 1ABC A B C 中， 1BB AB 又 AB BC 且 1BC BB B ∴ AB⊥平面 B1BCC1，又 CH 平面 B1BCC1······················································ 8 分 ∴ AB⊥CH 又 CH⊥BE， BE AB B ∴ CH ABE 平面 ························································································ 9 分 ∴ D 到平面 ABE 的距离为 1 2 CH ····································································· 10 分 在正方形 B1BCC1 中，又 BB1=BC=2 ∴ 1 1 22BCES BC CC     又 1 52BCES CH    ∴ 4 55CH  ····························································· 11 分 ∴ 所求距离为 2 5 5 ·······················································································12 分 方法二 设点 D 到平面 ABE 的距离为 d ∵ D 是 AC 的中点，且 , AB BC 2AB BC  ∴ 1 1 1 2 2 12 2 2ABD ABCS S     △ △ ·································································· 7 分 由 E 平面 1 1 1A B C 及直棱柱的性质知，E 到平面 ABD 的距离＝ 1 2AA  ························ 8 分 ∴ 1 223 3E ABD ABDV S   △ ··············································································9 分 由直棱柱的性质知： 1 1 1, BB B E BB AB  又 , AB BC 且 1BC BB B ∴ AB⊥平面 B1BCC1·····················································································10 分 又 BE  平面 B1BCC1 故 AB BE ∴ 2 2 2 2 1 1 1 1 2 2 1 52 2ABES AB BE BB B E         △ ····································11 分 ∵ 1 3E ABD D ABE ABEV V dS   △ ∴ 3 2 52 55 E ABD ABE Vd S    △ ·············································································12 分 20、解： （1）设椭圆 1C 的焦点坐标为 0)0,(  cc ∴ 2c ， 又 2 2 ce a  ············································································ 1 分 ∴ 2a ， 又 2222  cab ， ∴ 2b ·················································3 分 ∴ 1C 的方程为 22 14 2 yx   ··············································································· 4 分 （2）法一：设 (1, )N m 由已知得， 0PQk  ，设 1 1 2 2( , ), ( , )P x y Q x y ∴ 1 2 1 22, 2x x y y m    ················································································6 分 又         124 124 2 2 2 2 2 1 2 1 yx yx 两式相减得： 2 1 12 12 12 12    xx yy xx yy ········································ 8 分 共 5 页 第 4页 ∴ 1 2PQk m  ······························································································· 9 分 ∴ 直线 l 的方程为 2 ( 1)y m x m   ，即 (2 1)y m x  ·············································10 分 取 2 1x ，则 0y ，故点 )0,2 1( 在直线l 上·························································11 分 ∴ 直线 l 过 1( , 0)2 ·························································································12 分 法二：由已知得， 0PQk  ，设 1 1 2 2( , ), ( , )P x y Q x y 设直线 PQ 的方程为  x my t ············································································ 6 分 由已知有 2 2 14 2       x y x my t ∴ 2 2 2( 2) 2 4 0    m y mty t ··············································································8 分 由 0  得 2 22 4 0  m t ∴ 1 2 2 2 2    mty y m ， 1 2 1 2( ) 2 2    x x m y y t ∴ 2 2 2 m t ∴ 1 2 , (1, )2   my y m N ····················································································· 10 分 ∴直线 PQ 的中垂线 l 的方程为 ( 1)2   my m x 即 1( )2  y m x ∴ 直线 l 过 1( , 0)2 ·························································································12 分 法三：当直线 PQ 斜率存在且不为 0 时，设 PQ 直线方程为  y kx m 由已知有 2 2 14 2       x y y kx m ∴ 2 2 2(2 1) 4 2 4 0    k y kmx m ·········································································· 8 分 由 0  得 2 24 2 0  k m 2 1 2 2 4 2 1 12, 2 22 1          km kx x m kk kk 1 2 1 2 1( ) 2 2( )       y y k x x m k m k ································································· 10 分 1(1, )2 N k ∴ 直线 l ： 1 1 ( 1)2   y xk k 即 1 1( )2  y xk ∴ 直线 l 过 1( , 0)2 ·························································································11 分 当直线 PQ 斜率不存在时， 1( , 0)2 也在 l 上 综上： 直线 l 过 1( , 0)2 ···················································································· 12 分 21、解： （1）当 0a  时， ( ) 1xf x e x   ， x  R ； ( ) 1xf x e   ··················································1 分 由 ( ) 0f x  得 0x  ··························································································· 2 分 当 ( , 0)x   时 ( ) 0f x  ， ( )f x 单调递减······························································3 分 共 5 页 第 5页 当 (0, )x    时 ( ) 0f x  , ( )f x 单调递增······························································4 分 ∴ min( ) (0) 0f x f  ·······················································································5 分 （2）由已知得： ( ) 1 2xf x e ax    ， (0) 0f   ， (0) 0f  ∴ ( ) 2xf x e a   ， 0x ≥ ················································································ 6 分 ① 当 1 2a ≤ 时， [0, )x    ， ( ) 0f x ≥ ， ( )f x 在单增·········································· 7 分 ∴ ( ) 0f x ≥ ，故 ( )f x 单增·········································································8 分 ∴ ( ) (0) 0f x f ≥ 恒成立···········································································9 分 ② 当 1 2a  时，若 [0, ln 2 )x a ，则 ( ) 0f x  ，此时 ( )f x 单调递减 又 (0) 0f   ∴ 当 [0, ln 2 )x a 时 ( ) 0f x  ·················································10 分 故 ( )f x 在[0, ln 2 )a 上单调递减，此时 ( ) (0) 0f x f ≤ ∴ ( ) 0f x ≥ 在[0, )  不能恒成立····························································11 分 综上可知，实数 a 的取值范围为 1( , ]2 ······························································12 分 22、解： （1）∵ 2sin cos   ∴ 2 2sin cos    ······················································································· 1 分 又 cos , sinx y     ······················································································2 分 ∴ C 的直角坐标方程为 2y x ·········································································· 4 分 （2）将 3 2: 1 2 x a t l y t      （t 为参数）代入 2y x 得： 2 2 3 4 0t t a   由 0a  知： 12 16 0a  △ ················································································ 5 分 设 1 2, t t 是方程 2 2 3 4 0t t a   的两根，则 1 2 1 2 2 3 4 0 t t t t a       ··········································6 分 ∴ 1 2 1 2 1 2 1 2 1 2 | | | | | |1 1 1 1 | | | | | | | | | | | | t t t t PM PN t t t t t t       ····················································7 分 = 2 1 2 1 2 1 2 ( ) 4 12 16 1| | 4 t t t t a t t a     ····················································8 分 ∴ 1 2a   或 3 2a  ··························································································· 9 分 0a 又 ∴ 3 2a  ······································································································ 10 分 23、解： （1）∵ ( ) | 1| | 3| | 1 3| 4f x x x x x       ≥ ·······························································1 分 由题意可知，即 24 6m m ≤ ，化简得： 2 2 0m m  ≤ ···········································2 分 解得： 1 2m ≤ ≤ ···························································································· 3 分 ∴ m 的取值范围为[ 1, 2] ··············································································· 4 分 （2）由（1）知： 0 2m  ，故 3 3 2a b  当 0b  时，由 3 2a  得： 3 2a  此时， 3 2a b  符合题意··················································································5 分 当 0b  时， ∵ 3 3 2 2 2 23( )( ) ( )[( ) ]2 4 ba b a b a ab b a b a b         ∴ 当 0b  时， 2 23( ) 02 4 ba b   ······································································· 6 分 共 5 页 第 6页 故由 3 3 2 0a b   知 0a b  ··············································································7 分 ∴ 3 3 2 2 22 ( )( ) ( )[( ) 3 ]a b a b a ab b a b a b ab          2 2 33 1( )[( ) ( ) ] ( )4 4a b a b a b a b     ≥ ·························································· 8 分 变形得： 3( ) 8a b ≤ ∴ 2a b ≤ ··································································································9 分 综上可知： 0 2a b  ≤ ···················································································10 分