2018届二轮复习4-7解三角形课件(全国通用)
4
.
7
解三角形
-
2
-
-
3
-
知识梳理
考点自测
1
.
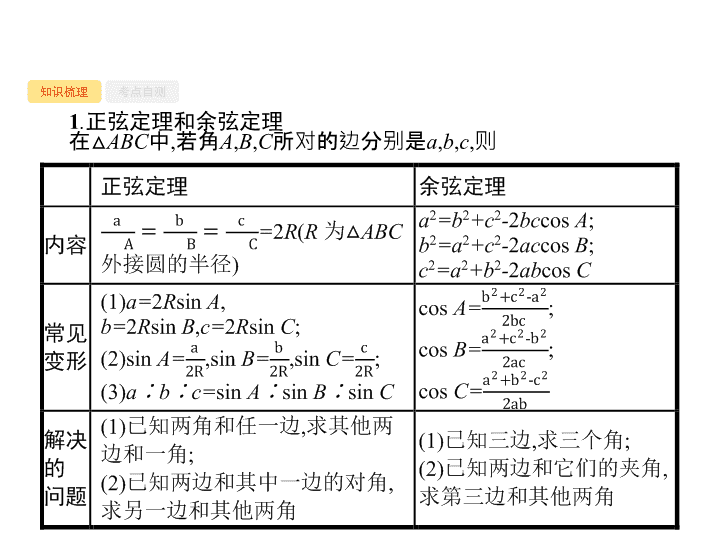
正弦定理和余弦定理
在
△
ABC
中
,
若角
A
,
B
,
C
所对的边分别是
a
,
b
,
c
,
则
-
4
-
知识梳理
考点自测
-
5
-
知识梳理
考点自测
3
.
实际问题中的常用角
(1)
仰角和俯角
:
与目标视线在同一铅垂平面内的水平视线和目标视线的夹角
,
目标视线在水平视线
的角叫做仰角
,
目标视线在水平视线
的角叫做俯角
(
如图
①
)
.
(2)
方向角
:
相对于某正方向的水平角
,
如南偏东
30
°
、北偏西
45
°
、西偏北
60
°
等
.
(3)
方位角
:
指从正北方向
转到目标方向线的水平角
,
如点
B
的方位角为
α
(
如图
②
)
.
(4)
坡度
:
坡面与水平面所成的二面角的度数
.
上方
下方
顺时针
-
6
-
知识梳理
考点自测
1
.
在
△
ABC
中
,
常有以下结论
(1)
A+B+C=
π
.
(2)
在三角形中大边对大角
,
大角对大边
.
(3)
任意两边之和大于第三边
,
任意两边之差小于第三边
.
(4)sin(
A+B
)
=
sin
C
;cos(
A+B
)
=-
cos
C
;tan(
A+B
)
=-
tan
C
;
(5)tan
A+
tan
B+
tan
C=
tan
A
·tan
B
·tan
C.
(6)
A>B
⇔
a>b
⇔
sin
A>
sin
B
⇔
cos
A<
cos
B.
2
.
用余弦定理判断三角形的形状
:
当
b
2
+c
2
-a
2
>
0
时
,
可知
A
为锐角
;
当
b
2
+c
2
-a
2
=
0
时
,
可知
A
为直角
;
当
b
2
+c
2
-a
2
<
0
时
,
可知
A
为钝角
.
-
7
-
知识梳理
考点自测
1
.
判断下列结论是否正确
,
正确的画
“
√
”,
错误的画
“
×
”
.
(1)
在
△
ABC
中
,
已知
a
,
b
和角
B
,
能用正弦定理求角
A
;
已知
a
,
b
和角
C
,
能用余弦定理求边
c.
(
)
(2)
在三角形中
,
已知两角和一边或已知两边和一角都能解三角形
.
(
)
(3)
在
△
ABC
中
,sin
A>
sin
B
的充分不必要条件是
A>B.
(
)
(4)
在
△
ABC
中
,
a
2
+b
2
0,
解得
b=
3,
故选
D
.
-
9
-
知识梳理
考点自测
-
10
-
知识梳理
考点自测
4
.
(2017
全国
Ⅲ
,
文
15)
△
ABC
的内角
A
,
B
,
C
的对边分别为
a
,
b
,
c.
已知
C=
60
°
, ,
c=
3,
则
A=
.
5
.
(2017
全国
Ⅱ
,
文
16)
△
ABC
的内角
A
,
B
,
C
的对边分别为
a
,
b
,
c
,
若
2
b
cos
B=a
cos
C+c
cos
A
,
则
B=
.
75
°
-
11
-
考点一
考点二
考点三
考点四
例
1
(2017
山东淄博二模
,
文
16)
△
ABC
的内角
A
,
B
,
C
的对边分别为
a
,
b
,
c
,
已知
2cos
A
(
c
cos
B+b
cos
C
)
=a.
(1)
求
A
;
利用正弦定理、余弦定理解三角形
-
12
-
考点一
考点二
考点三
考点四
-
13
-
考点一
考点二
考点三
考点四
思考
已知怎样的条件能用正弦定理解三角形
?
已知怎样的条件能用余弦定理解三角形
?
解题心得
1
.
已知两边和一边的对角或已知两角和一边都能用正弦定理解三角形
.
正弦定理的形式多样
,
其中
a=
2
R
sin
A
,
b=
2
R
sin
B
,
c=
2
R
sin
C
能够实现边角互化
.
2
.
已知两边和它们的夹角、已知两边和一边的对角或已知三边都能直接运用余弦定理解三角形
,
在运用余弦定理时
,
要注意整体思想的运用
.
3
.
已知两角和一边
,
该三角形是确定的
,
其解是唯一的
;
已知两边和一边的对角
,
该三角形具有不唯一性
,
通常根据三角函数值的有界性和大边对大角定理进行判断
.
-
14
-
考点一
考点二
考点三
考点四
对点训练
1
在
△
ABC
中
,
∠
A=
60
°
,
c= a.
(1)
求
sin
C
的值
;
(2)
若
a=
7,
求
△
ABC
的面积
.
-
15
-
考点一
考点二
考点三
考点四
判断三角形的形状
例
2
在
△
ABC
中
,
a
,
b
,
c
分别为内角
A
,
B
,
C
的对边
,
且
2
a
sin
A=
(2
b-c
)sin
B+
(2
c-b
)sin
C.
(1)
求角
A
的大小
;
(2)
若
sin
B+
sin
C=
,
试判断
△
ABC
的形状
.
解
(1)
由
2
a
sin
A=
(2
b-c
)sin
B+
(2
c-b
)sin
C
及正弦定理
,
得
2
a
2
=
(2
b-c
)
b+
(2
c-b
)
c
,
即
bc=b
2
+c
2
-a
2
,
-
16
-
考点一
考点二
考点三
考点四
-
17
-
考点一
考点二
考点三
考点四
思考
判断三角形的形状时主要有哪些方法
?
解题心得
判断三角形的形状时主要有以下两种方法
:
(1)
利用正弦定理、余弦定理把已知条件转化为边边关系
,
通过因式分解、配方等得出边的相应关系
,
从而判断三角形的形状
;
(2)
利用正弦定理、余弦定理把已知条件转化为内角的三角函数间的关系
,
通过三角恒等变换
,
得出内角的关系
,
从而判断出三角形的形状
,
此时要注意应用
A+B+C=
π
这个结论
.
-
18
-
考点一
考点二
考点三
考点四
对点训练
2
(2017
广东、江西、福建十校联考
,
文
17)
在
△
ABC
中
,
内角
A
,
B
,
C
所对的边长分别是
a
,
b
,
c.
(2)
若
sin
C+
sin(
B-A
)
=
sin 2
A
,
试判断
△
ABC
的形状
.
-
19
-
考点一
考点二
考点三
考点四
-
20
-
考点一
考点二
考点三
考点四
正弦定理、余弦定理与三角变换的综合问题
-
21
-
考点一
考点二
考点三
考点四
-
22
-
考点一
考点二
考点三
考点四
思考
在三角形中进行三角变换要注意什么
?
解题心得
1
.
在三角形中进行三角变换要注意隐含条件
:
A+B+C=
π
,
使用这个隐含条件可以减少未知数的个数
.
2
.
在解三角形问题中
,
因为面积公式
S= ab
sin
C= bc
sin
A= ac
sin
B
中既有边又有角
,
所以要和正弦定理、余弦定理联系起来
;
要灵活运用正弦定理、余弦定理实现边角互化
,
为三角变换提供了条件
.
-
23
-
考点一
考点二
考点三
考点四
-
24
-
考点一
考点二
考点三
考点四
-
25
-
考点一
考点二
考点三
考点四
例
4
设
△
ABC
三个角
A
,
B
,
C
的对边分别为
a
,
b
,
c
,
向量
p
=
(
a
,2
b
),
q
=
(sin
A
,1),
且
p
∥
q
.
(1)
求
B
的大小
;
(2)
若
△
ABC
是锐角三角形
,
m
=
(cos
A
,cos
B
),
n
=
(1,sin
A-
cos
A
tan
B
),
求
m
·
n
的取值范围
.
-
26
-
考点一
考点二
考点三
考点四
-
27
-
考点一
考点二
考点三
考点四
-
28
-
考点一
考点二
考点三
考点四
正弦定理、余弦定理在实际问题中的应用
例
5
如图
,
一辆汽车在一条水平的公路上向正西方向行驶
,
到
A
处时测得公路北侧一山脚
C
在西偏北
30
°
的方向上
,
行驶
600 m
后到达
B
处
,
测得此山脚
C
在西偏北
75
°
的方向上
,
山顶
D
的仰角为
30
°
,
则此山的高度
CD=
m
.
-
29
-
考点一
考点二
考点三
考点四
-
30
-
考点一
考点二
考点三
考点四
思考
利用正弦定理、余弦定理解决实际问题的一般思路是什么
?
解题心得
利用正弦定理、余弦定理解决实际问题的一般思路
:
(1)
实际问题经抽象概括后
,
已知量与未知量全部集中在一个三角形中
,
可用正弦定理或余弦定理求解
;
(2)
实际问题经抽象概括后
,
已知量与未知量涉及两个或两个以上的三角形
,
这时需作出这些三角形
,
先解够条件的三角形
,
再逐步求解其他三角形
,
有时需设出未知量
,
根据条件列出方程
(
组
),
解方程
(
组
)
得出所要求的解
.
-
31
-
考点一
考点二
考点三
考点四
对点训练
5
(2017
福建福州一模
,
文
15)
如图
,
小明同学在山顶
A
处观测到
,
一辆汽车在一条水平的公路上沿直线匀速行驶
,
小明在
A
处测得公路上
B
,
C
两点的俯角分别为
30
°
,45
°
,
且
∠
BAC=
135
°
.
若山高
AD=
100 m,
汽车从点
B
到点
C
历时
14 s,
则这辆汽车的速度为
m/s
.
(
精确到
0
.
1 m/s)
22
.
6
-
32
-
考点一
考点二
考点三
考点四
-
33
-
考点一
考点二
考点三
考点四
1
.
正弦定理和余弦定理其主要作用是将已知条件中的边、角关系转化为角的关系或边的关系
.
2
.
在已知关系式中
,
既含有边又含有角
,
通常的解题思路
:
先将角都化成边或将边都化成角
,
再结合正弦定理、余弦定理即可求解
.
3
.
在
△
ABC
中
,
已知
a
,
b
和
A
,
利用正弦定理时
,
会出现解的不确定性
,
一般可根据
“
大边对大角
”
来取舍
.
1
.
在解三角形中
,
三角形内角和定理起着重要作用
,
在解题中要注意根据这个定理确定角的范围
,
确定三角函数值的符号
,
防止出现增解等扩大范围的现象
.
2
.
在判断三角形的形状时
,
等式两边一般不要约去公因式
,
应移项提取公因式
,
以免漏解
.